Статистические методы исследования точности

4.11.1. Кривые распределения и оценка точности обработки

Построение кривых распределения производит ся следующим образом. Всю совокупность измерений интересующей нас величины (например, какого-либо размера в партии заготовок, обработанных при определенных условиях) разбивают на ряд групп. В каждую группу входят величины, результаты измерения которых находятся в пределах установленного интервала. Интервалы, число которых обычно берут в пределах 7-11, откладывают по оси абсцисс, а количество замеров, приходящееся на каждый интервал – по оси ординат. После соединения нанесенных на график точек получают ломаную линию, называемую полигоном распределения. На рис. 34,апоказан полигон распределения диаметральных размеров колец, подвергнутых предварительному обтачиванию, из которого видно, что на средние интервалы размеров приходится большее количество колец. При увеличении количества деталей в партии, сужении интервалов и увеличении их числа ломаная линия приближается к плавной кривой.

Вместо абсолютного количества mдеталей в каждом интервале по оси ординат откладывают также отношение этого количества к общему количеству nдеталей в партии; данное отношение называется относительной частотой, или частостью.

В качестве самой приближенной меры точности исследуемого процесса обработки может служить поле рассеяния размеров. Величину поля рассеяния можно брать по полигону распределения или по таблице измерения исследуемых значений. Чем ужеполе рассеяния, тем точнее исследуемый технологический метод.

Вид кривой распределения определяется количеством и характером факторов, влияющих на исследуемую величину. Многочисленные исследования показали, что в технологии машиностроения распределение размеров чаще всего происходит по так называемому «нормальному» закону или закону Гаусса. Соответствующая кривая распределения имеет симметричную шатрообразную форму (рис. 34,б).

Нормальный закон распределения имеет место в тех случаях, когда исследуемая случайная величина является результатом действия большого числа различных факторов по интенсивности своего влияния и действует одинаково. Этому закону подчиняются многие случайные непрерывные величины: размеры деталей, обработанных на настроенных станках; вес заготовок и деталей машин; твердость и др. характеристики материала; высота микронеровностей на обработанных поверхностях; погрешности измерения и некоторые др. величины. Практически почти всегда во всех перечисленных случаях приходится наблюдать небольшие отклонения от нормального закона. Эти отклонения обычно не постоянны во времени для номинально одних и тех же условий обработки. Кривая Гаусса выражается следующим уравнением:

,

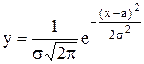где s – среднее квадратичное отклонение аргумента;

е – основание натуральных логарифмов;

а – значение абсциссы, при которой ордината у кривой достигает максимума; величина «а» является центром распределения (группирования) аргумента и в то же время его средней арифметической.

Закон Гаусса двухпараметрический (параметры б и а).

Ордината вершины кривой при х = а:

У_max =.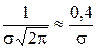

Точки перегиба кривой лежат на расстояниях «а» от ее оси симметрии (рис. 34,б).

Величина среднего квадратичного отклонения s, являющаяся мерой точности, характеризует форму кривой распределения. При больших значениях s кривая получается очень пологой и поле рассеяния растет. При малых значениях s точность исследуемого метода повышается и кривая получается сильно вытянутой вверх с малым полем рассеяния. На рис. 34,в показаны кривые распределения диаметральных размеров цилиндрического отверстия на различных этапах его обработки. Кривая s характеризует распределение размеров отверстия в исходной заготовке; кривая s₁– распределение размеров после предварительной обработки, а кривые s₂ и s₃– соответственно после чистовой и окончательной обработок. При правильном построении технологического процесса обработки необходимо выполнять условие s>s₁>s₂>s₃, так как на каждом последующем переходе обработки должна обеспечиваться более высокая точность, чем на предыдущем. Кроме того, величины х₃–х₂, х₂–х₁и х₁–хдолжны быть достаточно большими во избежание брака при обработке.

Кроме закона Гаусса встречаются и другие законы распределения размеров обработанных деталей в партии. Например, закон треугольника (Симпсона), закон Шарлье.

4.11.2. Точечные диаграммы и их применение для исследования точности обработки

Другой метод исследования точности основан на построении точечных диаграмм. По горизонтальной оси откладывают номера обрабатываемых деталей в той последовательности, как они сходят со станка. По вертикальной оси в виде точек откладывают результаты измерений деталей. Подобные диаграммы можно строить как для одной, так и для нескольких последовательно обрабатываемых партий деталей (рис. 35,а).

Длину подобных диаграмм можно значительно сократить, если по горизонтальной оси откладывать не номера заготовок, а номера групп деталей, причем в каждую группу должно входить одинаковое количество последовательно снимаемых со станка деталей (рис. 35,б).

На рис. 35,в показана диаграмма, по вертикальной оси которой откладываются средние арифметические значения размеров деталей, входящих в каждую группу. В данном случае гораздо легче уловить общую тенденцию изменения выполняемых размеров с течением времени.

На рис. 35,в отчетливо видна периодичность изменения размеров в результате непрерывно протекающего износа режущего инструмента и периодически производимых поднастроек станка.

Свойства точечных диаграмм стали следует подробно изучать в связи с развитием и применением в промышленности статистического метода контроля продукции. Сущность этого метода заключается в том, что в процессе изготовления данной продукции периодически берут пробы в количестве от двух до десяти деталей. Результаты измерений этих деталей, производимых универсальными инструментами, немедленно обрабатывают и наносят на специальную (контрольную) диаграмму. На этой диаграмме предусмотрены параллельные прямые а,определяющие границы поля допуска, и прямые б, определяющие поле рассеяния средних групповых значений и называющиеся контрольными прямыми.

в)

б)

г)

а)

Место контрольных прямых находят на основе теоретических положений статистического контроля, рассматриваемых в специальных курсах и литературе. На рис. 35,гв качестве примера показан образец диаграммы с нанесенными результатами контроля. Точки, соответствующие средним групповым значениям, соединены линиями. Вначале процесс обработки протекает нормально и ломаная линия не выходит за пределы контрольных прямых. При контроле группы А установлен выход ломаной линии за пределы контрольных границ. Это служит сигналом для поднастройки станка, регулированием или сменой инструмента, или проверкой положения упоров.

5. ПРИПУСКИ НА МЕХАНИЧЕСКУЮ ОБРАБОТКУ

Чертёж исходной заготовки отличается от чертежа детали тем, что содержит запас материала, который необходимо снять для обеспечения требуемых размеров и формы детали.

Форма поверхностей заготовок определяется технологией их получения, требующей в ряде случаев определённых углов и закруглений (штамповка, литьё).

ГОСТ 31109-82 определяет понятие припуска.

Общим припуском на механическую обработку называют слой металла, удаляемый с поверхности исходной заготовки в процессе механической обработки с целью получения исходной заготовки.

Примечание. Исходной заготовкой называют заготовку, используемую на первой операции механической обработки, то есть заготовку, ещё не подвергнутую никакой обработке.

Установление правильных размеров припусков на обработку является важной технико-экономической задачей. Назначение чрезмерно больших припусков ведёт к производительным потерям материала, превращаемого в стружку, к увеличению трудоёмкости обработки, повышению износа режущего инструмента, увеличению потребности в рабочей силе и оборудовании, кроме того, при чрезмерно больших припусках сложно использовать метод автоматического получения размеров, также сложно подбирать приспособления, обеспечивающие требуемую точность. Назначение недопустимо больших припусков не обеспечивает удаление дефектных слоёв материала и достижение требуемой точности и шероховатости, а также повышает требования к точности исходных заготовок и приводит к их удорожанию. А в случае очень малого припуска может привести к появлению брака.

Операционный припуск – слой материала, удаляемый с заготовки за одну технологическую операцию. Операционный припуск равен сумме промежуточных припусков, то есть припусков, снятых на каждом последующем переходе. Для наглядности расчёта и определения припуска пользуются схемами расположения припусков. На схеме показываются в условном масштабе (соблюдая пропорциональность) величины и взаимное расположение припусков и допусков.

Пример 8. Построить схему расположения припусков, полученную при обработке вала в две стадии: 1 – точение, 2 – шлифование.

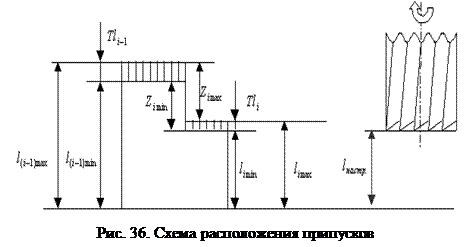Исходная заготовка имеет допуск, равномерный от номинала, а готовая деталь имеет допуск в системе вала,то есть в минус (рис. 36).

Общий номинальный (расчётный) припуск на обработку есть разница номинальных размеров исходной заготовки и готовой детали:

.

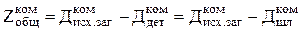Он же равен сумме номинальных припусков на отдельных операциях или переходах:

,

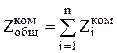где n – число операций или переходов.

Из приведённой формулы видно, что следует различать минимальный операционный припуск 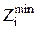– разность наименьшего предельного размера до обработки и наибольшего предельного размера после обработки на данной операции:

.

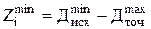Максимальный операционный припуск 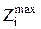– разность между наибольшим диаметром до обработки и наименьшим диаметром после обработки:

.

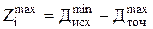Из схемы расположения припусков видно, что для определения максимального припуска следует к минимальному операционному припуску прибавить допуски для предшествующей и последующей операций (или переходов),

.

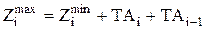Допуск припуска – разность пределов расстояний между максимальным и минимальным значениями размера припуска. Номинальный операционный припуск-разность номинальных размеров до и после обработки на данной операции:

.

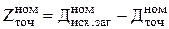Для определения номинального припуска на первой операции обработки для заготовок имеющих симметричное расположение поля допуска в расчёт 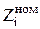, принимается не всё поле допуска, а только его часть, направленная в тело (в «–»):

.

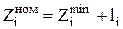При ориентировочных расчётах припусков можно использовать следующее соотношение:

.

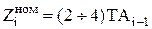Приведённые схемы и формулы показывают, что расширение допусков для предыдущих операций, неизбежно вызывает увеличение припуска на последующих операциях, следовательно, снижается производительность обработки. При уменьшении припуска на какую-то операцию следует повышать точность, а следовательно, и стоимость предыдущей заготовки. В связи с этим при назначении операционных припусков необходимо решить следующие технико–экономические задачи:

1. Операционный припуск должен быть не большим, чтобы не удорожать данную операцию, но и не малым,чтобы не удорожать заготовку.

2. Допуск должен быть достаточно широким для обеспечения выполнения данной операции и его максимальная ширина должна ограничиваться тем, чтобы не вызвать чрезмерного увеличения припуска на последующих операциях.

Для расчета схемы припуска используют следующую последовательность:

1. Определяют минимальный припуск, который требуется для получения конечного размера, то есть размера детали, затем определяют максимальную величину припуска на каждой операции и рассматривают величину допуска предшествующей операции, который сравнивают с допусками возможной заготовки для данных условий производств.

2. Наименьший операционный припуск складывается из определённых элементов, связанных с погрешностями,

,

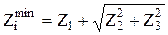где Z₁ – слой металла, который необходим для устранения неровностей и дефектного слоя предыдущей операции;

Z₂ – слой металла, удаляемый для компенсации погрешности формы и пространственных отклонений обрабатываемых поверхностей относительно базовых (рис. 37);

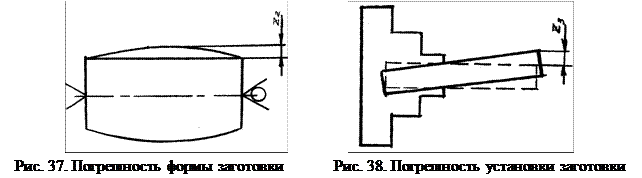Z₃ – слой металла, удаляемый для компенсации погрешности установки заготовки в приспособлении (рис.38). В данном случае погрешность рассматривается с позиции её влияния на смещение и поворот обрабатываемых поверхностей при установке и закреплении заготовки (не следует путать с погрешностью установки w_у с позиции влияния на суммарную погрешность размеров).

Величины Z₂ и Z₃ определяются экспериментально либо аналитически. Экспериментальное определение возможно только в конкретных условиях установки обрабатываемых заготовок.

Примечание. При расчёте припусков в курсовом и дипломном проекте следует использовать статичный способ. Однако когда нет значений составляющих тех или иных формул для расчёта Z_min, можно брать аналогичное, ссылаясь на производственный опыт.

При обработке плоскостей значение Z_min рассчитывается как простая арифметическая сумма:

.

Значения величин Rz, h, Z₂, Z₃ приводятся в справочной литературе.

Примечание. При выполнении расчёта припуска можно пользоваться литературой [1, 4] Расчётно-статический метод определения припусков и промежуточных размеров принят массово в крупносерийном производстве и в других видах производства для ответственных деталей. При единичном и серийном производстве для деталей средней точности при определении общих и операционных припусков используют таблицы нормативных припусков. Они разработаны на основе изучения практического опыта и могут быть использованы для средних условий производства. Использование этих таблиц ускоряет процесс проектирования, однако необходимо производить уточнения по конкретному изделию, для которого разрабатывается технология. Эти уточнения могут иметь следующий вид:

1. При обработке самоцентрирующимся инструментом, а также при бесцентровочном шлифовании Z₃=0, тогда .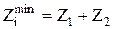

2. При полировании валов, когда не становится задача повышения точности, а требуется обеспечить шероховатость поверхности значения Z₂ и Z₃=0, .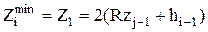

3. При чистовом шлифовании после ТО или предварительной мех обработке и при отсутствии дефектного слоя, когда ставится задача минимизировать шероховатости, Z₂=Z₃=0 и h=0, .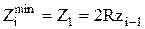

После определения Z^min рассматривается максимальное значение возможного при неблагоприятном сочетании промежуточных размеров, максимальный припуск рассчитывают по формуле

.

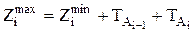Когда значение истинного припуска зависит от размеров, величина припуска может рассматриваться в качестве звена размерной цепи, составляющими звеньями которой являются размеры, влияющие на величину припуска:

;

.

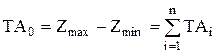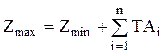Расчёт припуска может быть произведён по предельным размерам составляющих звеньев размерной цепи, рассчитанной по методу взаимозаменяемости, причём значения величины припуска в этих размерных цепях должны быть их замещающими звеньями (рис. 39):

,

,

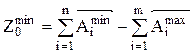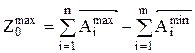где 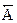– увеличивающее звено размерной цепи;

n – количество увеличивающих звеньев размерной цепи;

– уменьшающее звено размерной цепи;

m – число уменьшающих звеньев.

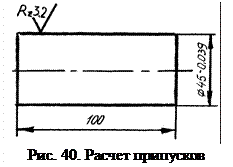Пример 9. Рассчитать припуски на обработку вала в диаметральном сечении, который должен быть получен из прутка методом горячего проката по ГОСТ 2590-75.

Требуется определить операционные припуски при последующей обработке и шлифовании (рис. 40).

Справочные данные следующие: заготовка, полученная горячим прокатом, имеет R_z=150мкм, Т=250мкм, eS=+0,4мм, l₁=0,7мм.

По источнику [12]: Z₂=6мкм, для обработки заготовки в центрах Z₃=0,36мм, тогда

;

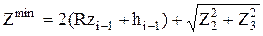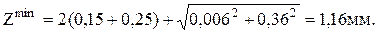
После точения глубина дефектного слоя h=30мкм, R_z=20мкм, Т=0,16мм.

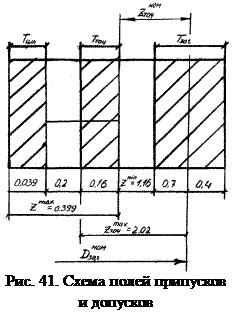
Z₂ равно диаметру, так как шлифование осуществляется в центрах, как при точении, и погрешность базирования равна 0,1мм:

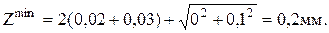
Строим схему полей припусков и допусков (рис. 41):

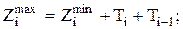
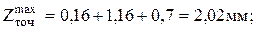
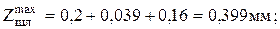
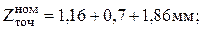
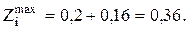
Затем необходимо рассчитать минимальный и максимальный диаметр точения, диаметр исходной заготовки и выбрать подходящий диаметр прутка для заготовки:

Д_исх._заг=45+1,86+0,36=47,22.

Принимаем ближайший диаметр прутка – 48 (+0,4.-0,7).

После этого пересчитывается реальный припуск на точение:

Примечание. Результатами расчётов допуска и межоперационных размеров должен быть минимально возможный размер при данной технологии.

Дата добавления: 2014-01-20