Первообразная функция. Определение и свойство неопределенного интеграла

Определение. Функция F(x) называется первообразной функцией (или просто первообразной) по отношению к функции f(x), если функция F(x) дифференцируема и удовлетворяет соотношению 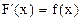или, что то же самое, .

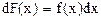Примеры:

1.Пусть, например, f(x)=2x, тогда функция 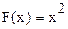есть первообразная для f(x)=2x, так как .

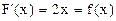2.Функция 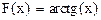является первообразной для функции 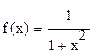на всей числовой оси, т.к. .

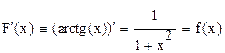3.Функция 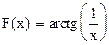является первообразной для функции 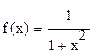как на полуоси всех положительных чисел, так и на полуоси всех отрицательных чисел, т.к. для x≠0

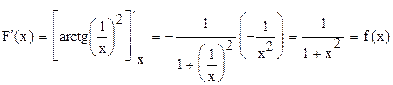
Утверждение. Есл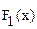и и 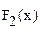- две первообразные функции f(x) на одном и том же промежутке, то их разность 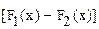постоянна на этом промежутке.

Доказательство:

По условию 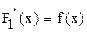и.

Следовательно,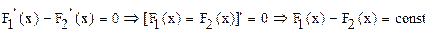

ч.т.д.

Как и операция взятия дифференцирования, имеющая свое название «дифференцирование» и свой математический символ 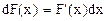, операция перехода к первообразной имеет свое название «неопределенное интегрирование» и свой математический символ

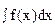, (1)

Называемый неопределенным интегралом от функции f(x) на заданном промежутке. В символе (1) знак 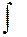называется знаком неопределенного интеграла, f(x) – подынтегральная функция, 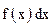– подынтегральное выражение, 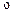– переменная интегрирования.

Из доказанного утверждения следует, что если F(x) – какая-нибудь конкретная первообразная функции f(x) на промежутке, то на этом промежутке любая другая первообразная может быть получена из конкретной F(x) добавлением некоторой постоянной.

Таким образом, символ (1) мы будем понимать как обозначение любой из первообразных функций f(x) на рассматриваемом промежутке.

Общее выражение всех первообразных называется неопределенным интегралом от f(x)

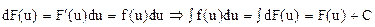
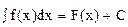, (2)

Из определения непосредственно вытекают следующие свойства неопределенного интеграла:

1.,

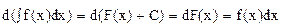Т.е. дифференциал от неопределенного интеграла равен подынтегральному выражению.

2.,

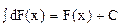Действительно, 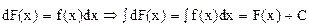, т.е. неопределенный интеграл от дифференциала некоторой функции равен этой последней функции плюс произвольная постоянная.

Свойства 1) и 2) устанавливают взаимность операции дифференцирования и неопределенного интегрирования. Эти операции взаимно обратные с точностью до появляющейся в свойстве 2) произвольной постоянной.

3),

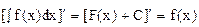Т.е. производная от неопределенного интеграла равна подынтегральной функции.

4)линейность неопределенного интеграла:

,

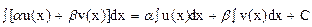Где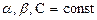; проверяется прямым дифференцированием с использованием свойства линейности дифференцирования (из свойства 3))

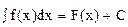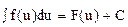5)Если, то, где 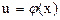- любая дифференцируемая функция.

Доказательство:

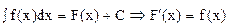
Рассмотрим теперь функцию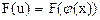; для ее дифференциала, в силу инвариантности вида первого дифференциала функции, имеем

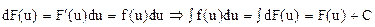
Ч.т.д.

Свойство 5) очень важно. Основная таблица интегралов в силу этого свойства оказывается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой дифференцируемой функцией ее.

Таким образом основная таблица сразу значительно расширяется.

Таблица неопределённых интегралов. Методы непосредственного интегрирования.

Подобно правилам дифференцирования, позволяющим дифференцировать линейные комбинации и композиции известных функций, основные свойства неопределённого интеграла позволяют в ряде случаев сводить отыскание первообразных одних функций к построению первообразных либо более простых функций, либо к уже известным первообразным. Набор таких известных первообразных может составить следующая краткая таблица неопределённых интегралов, полученная переписыванием таблицы производных основных элементарных функций.

1. 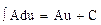, А=const

2.

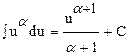
3.

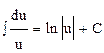
4.

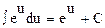
5. 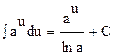, (0<а≠1)

6.

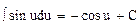
7.

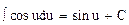
8.

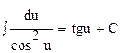
9.

10.

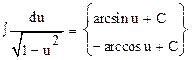
11.

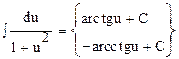
12.

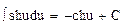
13.

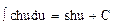
14.

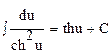
15.

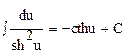
16.

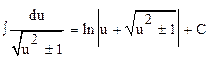
17.

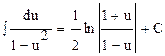
Каждая из этих формул рассматривается на тех промежутках вещественной оси, на которых определены соответствующие функции.

Примечание.

Операции дифференцирования и неопределённого интегрирования, как уже отмечалось, взаимно обратные. Причём, если прямая операция – дифференцирование – не выводит из того класса, где она применяется, то обратная операция – неопределённое интегрирование – может выводить из рассматриваемого класса. Например, если мы будем рассматривать класс элементарных функций. Очевидно, производная от любой элементарной функции будет снова элементарной функцией. Этого нельзя утверждать для неопределённого интеграла. Например, следующие интегралы не выражаются через элементарные функции:

1) 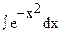- интеграл Пуассона

2) 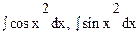- интегралы Френеля

3) 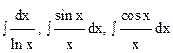- интегральный логарифм, интегральный синус, интегральный косинус. Эти интегралы существуют, но не являются элементарными функциями.

Дата добавления: 2014-01-20