Первообразные рациональных функций

Рассмотрим вопрос об интегралах вида ,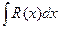

Где 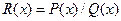- отношение двух полиномов.

Из курса алгебры известно, на множестве вещественных чисел любую такую дробь можно разложить в сумму следующего вида:

, (*)

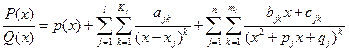Где p(x) – многочлен (он появляется при делении P(x) на Q(x) только если степень P(x) не меньше степени Q(x));

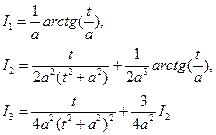
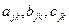- однозначно определяемые вещественные числа;

А многочлен Q(x) имеет вид

. (**)

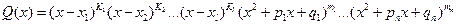Так как из неправильной рациональной дроби можно исключить целую часть, интегрирование которой не представляет трудностей, то достаточно рассмотреть вопрос об интегрировании правильных дробей, т.е. дробей, у которых степень числителя ниже степени знаменателя.

Из них остановимся на так называемых простых дробях; это будут дроби следующих видов:

1);

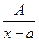2);

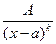3);

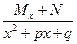4)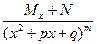, k, m=2,3,…

Где A, M, N, a, p, q – вещественные числа, кроме того по отношению к дробям вида 3 и 4 предполагают, что трехчлен 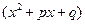не имеет вещественных корней, т.е. .

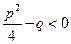Дроби видов 1 и 2 мы уже имеем интегрировать:

;

, .

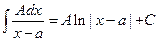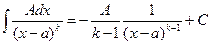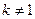Интегрирование дробей вида 3 и 4 облегчается подстановкой 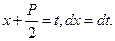(1). Для того, чтобы воспользоваться подстановкой (1)выделим из выражения 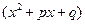полный квадрат.

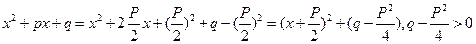
Получим 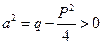и воспользуемся подстановкой (1). Получим:

;

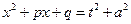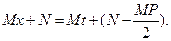
Для дроби вида 3 будем иметь

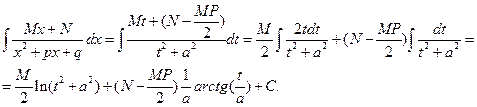
Возвращаясь теперь к старым переменным и учитывая, что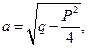

Получаем 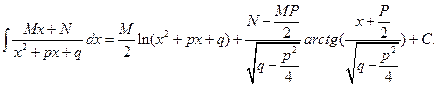(2)

Для дроби вида 4:

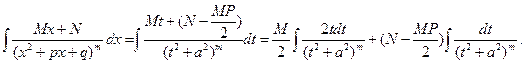(3)

Первый из интегралов справа в формуле (3) легко вычисляется подстановкой

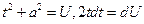
Будем иметь

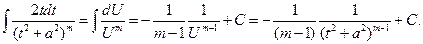(4)

Второй из интегралов справа в формуле (3), при любом m, может быть вычислен по рекуррентной формуле, а именно, применим к нему формулу интегрирования по частям.

Получим

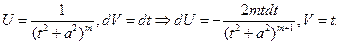
Таким образом,

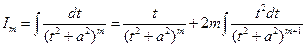(5)

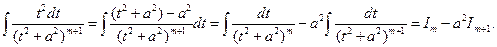
Подставив последнее соотношение в (5), получим

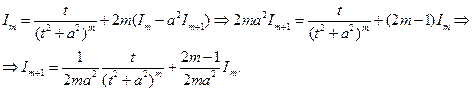. (6)

Очевидно,

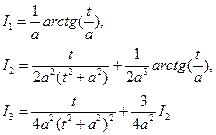
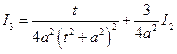, и т.д.

Таким образом, можно вычислить интеграл для любого натурального m. Окончательно останется лишь вернуться к старой переменной x, положив 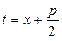. Этим исчерпывается вопрос об интегрировании простых дробей.

Дата добавления: 2014-01-20