
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разложение правильных дробей на простые
|
|
|
|
Из формул (*) и (**) видно, что разложение правильтной дроби на простые дроби тесно связано с разложением её знаменателя на множители. Как известно, каждый целый многочлен с вещественными коэффицентами разлагается (и при том единственным образом) на вещественные множители вида  и
и 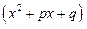 , причём квадратные множители предпологаются не имеющими вещественных корней. Объединяя одинаковые множители (если такие имеются) и пологая, для простоты, старший коэффициент Q(x), равным 1 можно записать разложение Q(x) в виде (**).
, причём квадратные множители предпологаются не имеющими вещественных корней. Объединяя одинаковые множители (если такие имеются) и пологая, для простоты, старший коэффициент Q(x), равным 1 можно записать разложение Q(x) в виде (**).
Таким образом, зная разложение (**), мы, тем самым, знаем знаменатели тех простых дробей, на которые разлагается данная дробь 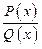 .
.
Для определения числовых коэффициентов в числителях простых дробей, обычно, используют метод неопределённых коэффициентов, который рассмотрим на примерах.
Пример:
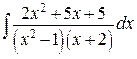
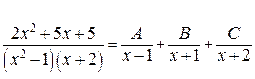 , приводим к общему знаменателю:
, приводим к общему знаменателю:
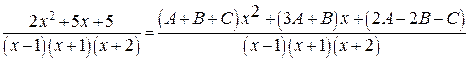
Приравниваем соответствующие коэффициенты числителей:
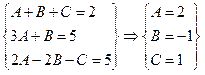
Итак, 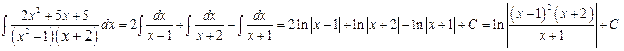
Интегрирование рациональных дробей.
Пример:
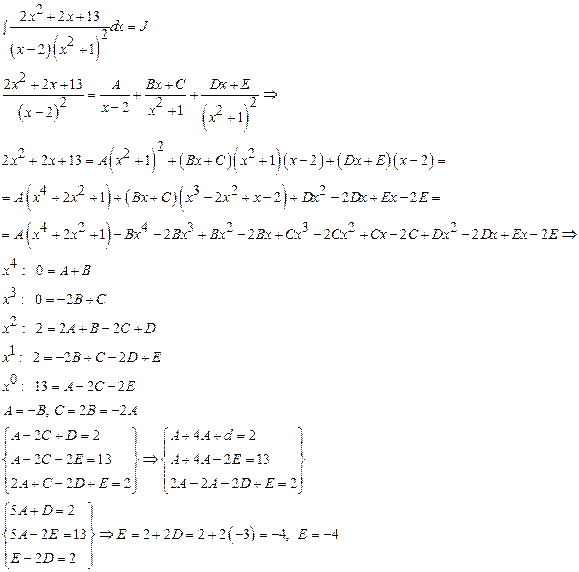
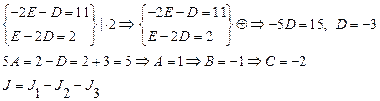
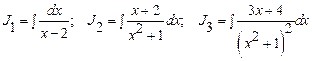
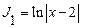
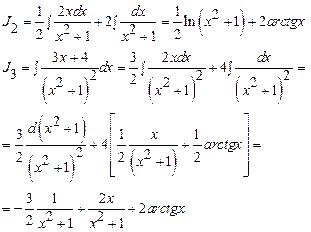
Первообразные вида 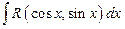
Воспользуемся подстановкой 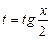 ,
, 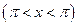
Имеем
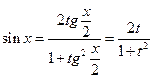
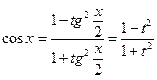

Таким образом,
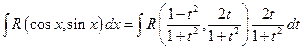
Указаннная подстановка является универсальной. Часть такой пусть приводит к очень громоздкой рациональной функции.
В ряде случаев существуют и другие возможности рацианализации исходного интеграла.
(1)В случае интегралов вида:
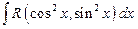
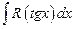
Удобна подстановка
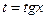
Действительно,
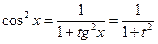
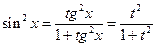
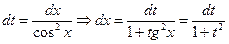
Таким образом,
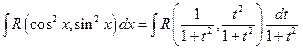
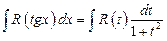
(2)В случае интегралов вида:
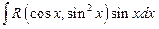 или
или 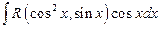
Можно внести функции sinx? Cosx под знак дифференциала и сделать замену t=cosx или t=sinx соответственно. После замены эти интегралы будут иметь вид:
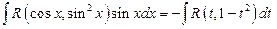
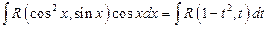
Примеры:
1)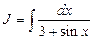 ;
; 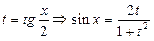 ,
, 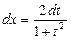
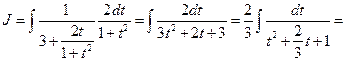
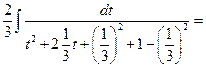
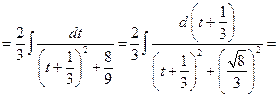
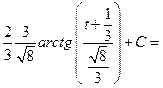
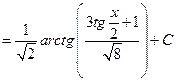
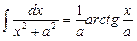 .
.
2)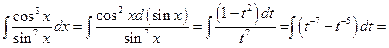
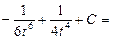
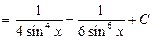 .
.
Первообразные вида 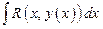
Если удастся сделать замену x=x(t) так, что обе функции x(t) и y=y(x(t)) окажутся рациональными функцмями от t, то 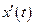 - тоже рациональная функция от t и
- тоже рациональная функция от t и 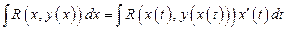 - интеграл от рациональной функции.
- интеграл от рациональной функции.
Рассмотрим некоторые существующие случаи:
Если
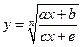 ,
, 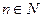
Делаем замену:
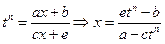 ,
, 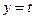
И таким образом подынтегральное выражение рационализируется.
Пример:
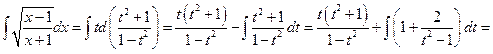
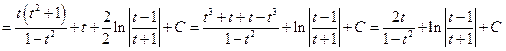 ,
,
где 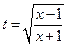 ,
, 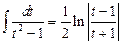 .
.
1)Рассмотрим теперь случай, когда 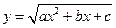 , т.е. рассмотрим интегралы вида:
, т.е. рассмотрим интегралы вида: 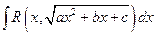 .
.
Выделяя полный квадрат в трёхчлене 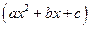 и делая соответствующую линейную замену переменной, сводим общий случай к однорму из следующих простейших.
и делая соответствующую линейную замену переменной, сводим общий случай к однорму из следующих простейших.
(*)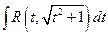 ,
, 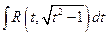 ,
, 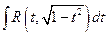 .
.
Для рационализации этих интегралов теперь достаточно положить соответственно:
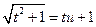 , или
, или 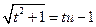 , или
, или 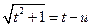 ;
;
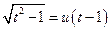 , или
, или 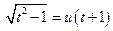 , или
, или 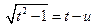 ;
;
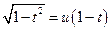 , или
, или 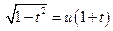 , или
, или 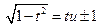 .
.
Эти подстановки были предложены Эйлером. Проверим, что после первой подстановки мы сведём первый интеграл к интегралу от рациональной функции. Действительно,
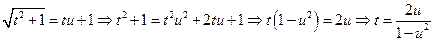 ;
;
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 537; Нарушение авторских прав?; Мы поможем в написании вашей работы!