Расчет конических закрытых передач с круговым зубом

1. Расчет диаметра шестерни и выбор основных параметров передачи.

Расчетный внешний диаметр шестерни, мм

,

где К_d – 90 МПа^1/3 – для передач с непрямым зубом;

К_ве- кэффициент ширины зубчатого венца относительно внешнего конусного расстояния К_ве = b/R_е = 0,2…0,3;

К_Нβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца- табл (НВ, расположение колес относительно опор, К_ве, u)

К_A – коэффициент внешней динамической нагрузки – табл.

коэффициент, учитывающий изменение прочности конических колес с непрямым зубом по сравнению с прочностью цилиндрических колес;

Конические зубчатые передачи – расчет

Зацепление двух конических колес можно рассматривать как качение без скольжения конусов с углами при вершинах 2δ₁ и 2δ₂. Эти конусы называются начальными. Применение получили передачи ортогональные с суммарным углом между осями δ₁ + δ₂ = 90^о. Конические зубчатые передачи выполняют без смещения исходного контура (х₁ = 0, х₂ = 0) или равносмещенными (х₁ = -х₂). При окружных скоростях до 3м/с применяют прямозубые колеса, при более высоких скоростях применяют передачи с круговыми зубьями.

Основные геометрические параметры:

1. Углы делительных конусов tqδ₁ = d_е1/d_е2 = Z₁/Z₂ =1/u; δ₂ = 90 – δ₁.

Модуль конического колеса меняется по длине зуба. За основной принимают окружной модуль на внешнем торце m_tе.

2.Внешние делительные диаметры: d_е1 = m_tе Z₁, d_е2 = m_tе Z₂.

3.Внешнее конусное расстояние: R_е = 0,5.

4. Конусное расстояние до середины зуба: R_m = R_e- 0.5b = R_e(1-0.5b/R_e) = R_e(1-0.5K_be). K_be = b/R_e < 0.35 (обычно 0,285)

4. Средний делительный диаметр и модуль находят из соотношения

d_m/d_e = (R_e – 0.5b) d_m = d_e(1 – 0.5K_be) m_m = m_te(1 – 0.5K_be)

6. Диаметр вершин зубьев: d_ae = d_e + 2h_aecosδ

При расчете на прочность конические колеса заменяют равнопрочными им цилиндрическими. Диаметр эквивалентного зубчатого колеса d_v = d_e/cosδ.

Эквивалентное число зубьев из зависимости mz_v = mz/cosδ равно Z_v = Z/cosδ,

для передач с круговыми зубьями 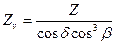.Параметры передачи угол профиля α = 20^о, коэффициенты высоты головки и ножки зуба h_а = 1, коэффициент радиального зазора С = 0,25, радиус скругления ρ_f = 0,25.

5. Силы действующие в зацеплении:

окружная сила на среднем делительном диаметре

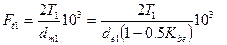Для шестерни прямозубой передачи F_r1 = F_vcosδ₁ = F_t1 tgα cosδ₁, F_a1 = F_vsinδ₁ = F_t1 tgα sinδ₁

Для шестерни с круговыми зубьями:

F_r1 = F_t1(tgα cosδ₁ ±sinβ_msinδ₁)/cos_m.

F_a1 = F_t1(tg α sinδ₁ ±sinβ_mcosδ₁)/cosβ_m

Для колеса: F_t2 = -F_t1.; F_r2 = -F_a1; F_a2 = -F_r1.

7.Расчет на прочность:

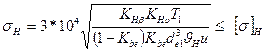,где 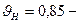для передач с прямым зубом; - для передач с круговым зубом.

Внешний делительный диаметр шестерни при К_bе = 0,285:

8. Проверочный расчет по напряжениям изгиба: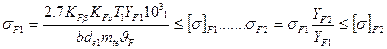, где υ_F = 0,85 – для прямозубых колес; υ_F = 0,94 + 0,08u при Н₁ = Н₂< 350НВ – для колес с круговым зубом.