
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Таблица основных неопределенных интегралов
|
|
|
|
Таблица основных неопределенных интегралов
Ранее мы получили таблицу производных основных элементарных функций. Каждая формула таблицы производных простейших элементарных функций, устанавливающая, что та или иная функция F(x) имеет производную f(x), приводит нас, в силу определения неопределенного интеграла, к соответствующей формуле интегрального исчисления
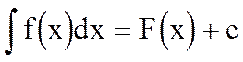 .
.
Таким образом, приходим к следующей таблице интегралов.
1. 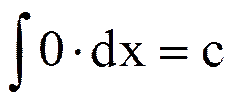
2. 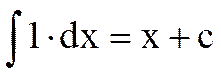
3. 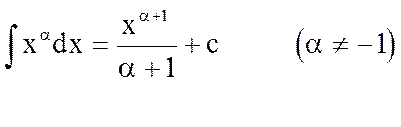
4. 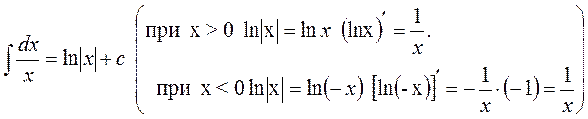
5. 
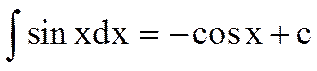
6. 
7. 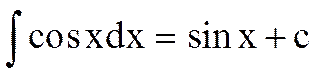
8. 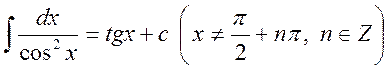
9. 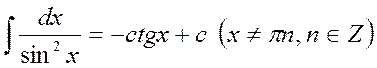
10. 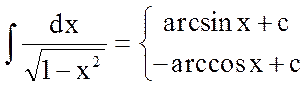
(-1<x<1)
11. 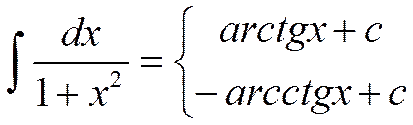
12. 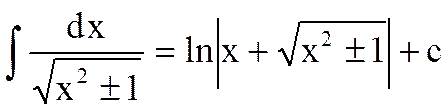 (½x½>1 в случае знака “-“)
(½x½>1 в случае знака “-“)
13. 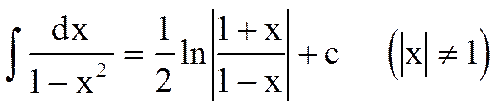
14. 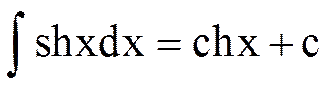
15. 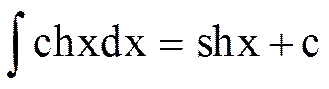
16. 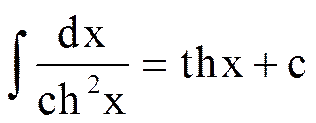
17. 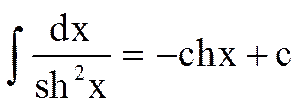
Замечание 1. Доказательство формул 12 и 13 следует провести непосредственным дифференцированием правых частей и проверкой совпадения результата с подынтегральными функциями слева.
Замечание 2. Операция дифференцирования не выводит нас из класса элементарных функций, однако можно доказать, что интегралы от некоторых элементарных функций уже не являются элементарными функциями, например,
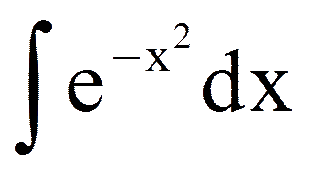
- интеграл Пуассона.
Теорема 2. Пусть функция j(х) определена и дифференцируема на множестве М. Пусть, далее, для функции g(u) существует первообразная функции G(u) на множестве 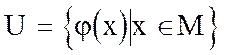 ,т.е
,т.е
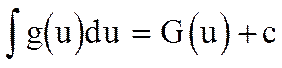 .
.
Тогда на множестве М для функции 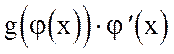 существует первообразная, равная G[j(x)], т.е.
существует первообразная, равная G[j(x)], т.е.
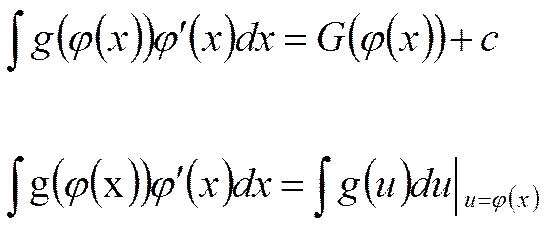 (1)
(1)
Доказательство. По теореме о производной сложной функции имеем
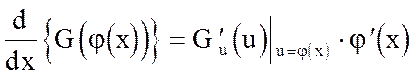 .
.
Но 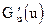 по определению первообразной есть g(u), поэтому
по определению первообразной есть g(u), поэтому
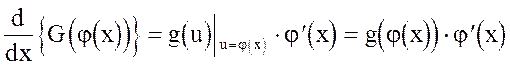 .
.
Таким образом, G(j(x)) является первообразной функции 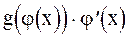 на множестве М, и формула (1) доказана.
на множестве М, и формула (1) доказана.
Существует два варианта метода замены переменной.
а) Метод подведения под знак дифференциала.
Пусть требуется вычислить интеграл 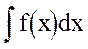 . Предположим, что существует дифференцируемая функция j(х) и функция g(u) такие, что подынтегральное выражение f(x)dx может быть записано в виде
. Предположим, что существует дифференцируемая функция j(х) и функция g(u) такие, что подынтегральное выражение f(x)dx может быть записано в виде
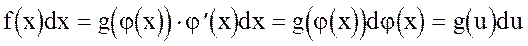 .
.
Это преобразование называется подведением j(х) под знак дифференциала. По теореме 2 имеем
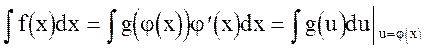
Поэтому вычисление 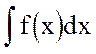 сводится к вычислению интеграла
сводится к вычислению интеграла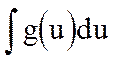 (который может оказаться проще исходного) и последующей подстановке u=j(x).
(который может оказаться проще исходного) и последующей подстановке u=j(x).
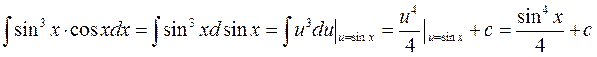
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 424; Нарушение авторских прав?; Мы поможем в написании вашей работы!