Рациональные функции от нескольких аргументов

Интегрирование некоторых иррациональностей

Определение 1. Многочленом степени n от двух аргументов x и y называется выражение вида

,

в котором через обозначены постоянные вещественные числа такие, что среди чисел есть хотя бы одно число, отличное от нуля.

Определение 2. Рациональной функцией от двух аргументов x и y называется выражение вида

,

где P_n(x,y) и Q_m(x,y) - многочлены от двух переменных степени n и m соответственно.

Утверждение. Если R(x,y) - рациональная функция от двух аргументов x и y, R₁(t), R₂(t), R₃(t) - три произвольных рациональных функции от одной переменной t, то выражение

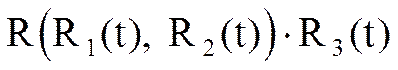
представляет собой рациональную функцию от одной переменной.

Замечание. В дальнейшем для доказательства интегрируемости в элементарных функциях некоторых выражений мы будем посредством специально подобранной подстановки сводить интеграл от рассматриваемых выражений к интегралу от рациональной дроби.

Дата добавления: 2014-01-20