Представление автоматов

Некоторые приемы приведения к грамматикам простого предшествования.

Грамматика для списков (которые очень часто встречаются): переменные, параметры, индексы.

<L>→λ

<L>→a<R>

<R>→, a<R>

<R>→λ

Предположим, что некоторая грамматика содержит такие 2 правила:

<S>→ if <B> then <S₁>

<S>→ if <B> then <S₁> else <S₂>

Эта грамматика не может быть LL(1) грамматикой, т.к. if содержится во множествах выбора обоих правил. При построении LL(1) грамматик важно, чтобы конструкции языка, начинающиеся с одинаковых символов, порождались одним общим для них правилом. Для рассматриваемого примера можно получить.

<S>→ if <B> then <S₁><нечто>

<нечто>→ else <S₂>|λ

Про такие правила говорят, что они получены из первоначальных двух методом «левой факторизации».

Грамматика с леворекурсивным нетерминалом не может быть LL(1) грамматикой. Грамматику с левой рекурсией всегда можно представить в грамматику без левой рекурсии. Основная идея состоит в том, чтобы смотреть на рекурсивный нетерминал как на порождающий некоторую цепочку, за которой следует список из одного или более элементов.

Например: <S>→<S>a

<S>→b

Трактуем нетерминал <S> как порождающий символ b, за которым следует список из нуля или символов a.

<A>→b<список>

<список>→a <список>|λ

Если приведенное выше правило преобразования объединить с заменой края, то его можно использовать для исключения леворекурсивности, даже когданекоторые леворекурсивные правила не являются самолеворекурсивными.

1.A→a<B>

2.A→ab

A→a<B><список>

A→abc<список>

A→<A>cb

<B>→ <A>b

<B>→d

<список>→cb<список>|λ

<B>→<A>

<B>→d

(Замена края:

Для правил

<A>→α₁

…

<A>→α_n­

<B>→ β<A>γ

<B>→βα₁γ

…

<B>→ βα_nγ)

Исключение λ-правил

Пусть есть две разновидности нетерминала А: < Ада >(с λ -правилами) и < Анет >

<S>→a<A><S> <S>→a<Анет><S>

<S>→b <S>→a<Ада><S>

<A>→c<S> <S>→b

<A>→λ <Aнет>→c<S>

<Aда>→λ (однозначное правило, которое можно исключить)

<S>→a<Анет><S>

<S>→a<S>

<S>→b

<Aнет>→c<S>

Можно опять перейти к нетерминалу A,но из него уже не выводима пустая цепочка.

<S>→a<A><S>

<S>→a<S>

<S>→b

<A>→c<S>

Общие правила в методике исключение λ -правил:

1. Определить, какие нетерминалы грамматики могут порождать пустую цепочку

2. Заменить каждое из правил, правые части которых содержат хотя бы по одному аннулирующему нетерминалу, множеством новых правил.

3. Исключить из грамматики все λ -правила, включая те, которые могли появиться на шаге 2.

Один из удобных способов представления КА – таблица переходов. КА с состояниями S₁,…,S_n и входными литерами Т₁,…,Т_n можно представить в виде матрицы В, состоящей из n x m элементов. Элемент B[i,j ] содержит число k – номер состояния S_k, такое что M[S_i,T_j]=S_k. Можно условиться, что состояние S₁ – начальное, а список заключённых состояний представлен вектором

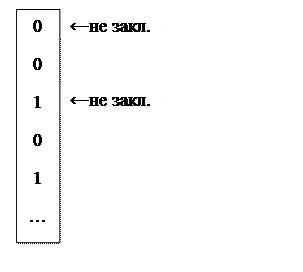
Такая матрица называется матрицей переходов, т.к. она указывает, каким образом происходит переключение из одного состояние в другое.

Другим способом представления может быть списочная структура. Представление каждого состояния с k дугами, исходящими из него, занимает 2k+2 слов. Первое слово – имя состояния, второе – значение k. Каждая последующая пара слов содержит терминальный символ из входного алфавита и указатель на начало представления состояния, в которое надо перейти по этому символу.

Дата добавления: 2014-01-11