Концевые маркеры и выходы из распознавания

Конечный распознаватель лежит в основе процессов распознавания цепочек в компиляторе. Один из способов использования такого распознавателя – поставить его под контроль некоторой управляющей программы, которая определяет момент, когда входная цепочка прочитана и по состоянию распознавателя выясняет допустима они или нет. Однако во многих приложениях требуется, чтобы распознаватель сам узнавал момент, когда задание выполнено. Поэтому таблица переходов в том виде, в каком она была рассмотрена, требует существенных изменений.

Рассмотрим следующий автомат:

	a	b
F	F F	F

Он допускает множество цепочек в алфавите { a; b }, таких, что символы в них либо не встречаются, либо встречаются парами. Например, этот автомат, допускает цепочки abb, abba, aaa, abbbbabb, bba и авторитет baa, abbb и abbab.

Очевидно, что в модели автомата не отражена идея «окончания» входной цепочки. Автомат нужно изменить так, чтобы он умел обрабатывать дополнительный символ - 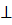- концевой маркер.

	a	b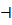
	F F	F	Да Нет Нет

Символ «Да» - это сокращённое указание на то, что работа закончена и автомат должен выйти на процедуру «Да». Новое состояние не наступает, т.к. на этом автомат свою работу заканчивает. С введением концевого маркера следует различать алфавит обрабатываемого языка и входной алфавит автомата, осуществляет обработку. В примере алфавит языка по прежнему { a, b } и концевой маркер в описании языка не участвует. Входным алфавитом автомата, распознающего этот язык, также остаётся { a, b }, но входной алфавит автомат, обрабатывающего тот же язык будет { a, b, }.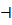

На практике многие конечные процессоры, применяемые в компиляторах, выполняют свои работы раньше, чем прочитана вся цепочка, т.е. не доходя до концевого маркера.

Допустим, нам нужно построить автомат, который при обнаружении первой же ошибки передаёт управление некоторой внешней процедуре, обрабатывающей ошибки. Эта процедура либо прерывает процесс обработки цепочки, либо восстанавливает нужное состояние и возобновляет обработку с целью обнаружения дальнейших ошибок. Так если наш автомат попал в состояние F, то входная цепочка будет отвергнута, и если мы решили прерывать работу автомата, как только обнаружена ошибка, то все переходы в состояние F в таблице переходов нужно заменить вызовами процедур «Нет».

	a	b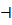
	Нет		Да Да

Состояние F удалено из автомата, т.к. отсутствие переходов в него означает, что автомат никогда не допускает этого состояния исходя из начального.

Допускаем теперь, что любой элемент таблицы переходов конечного процессора может быть не переходом, а выходом из распознавания. Этот процесс обработки входных цепочек назовём обнаружением (или детекцией). Детекция может встречаться при обработке как допустимых, так и ошибочных цепочек.

Дата добавления: 2014-01-11