Проверка эквивалентности двух состояний

Будем рассматривать автоматы с одним и тем же входным множеством.

Состояние S и t ~óкогда выполняются следующие условия:

1) Условия подобия – состояния S и t должны быть либо оба допускающими, либо оба отвергающими.

2) Условие преемственности - для всех входных символов состояния S и t должны переходить в эквивалентные состояния, т.е. их приемники ~.

Теперь покажем, что эти 2 условия выполняются ó когда S и t не имеют различающей цепочки.

=>) Заметим, что если нарушено хотя бы одно и них, то 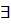цепочка, различающая эти 2 состояния. Если нарушено условие преемственности, то некоторый вводной символ х переводит состояние S и t в не эквивалентные состояния. Поэтому х с приписанной к нему цепочкой, различающей эти новые состояния образуют цепочку, различающую S и t.

<=) Теперь убедимся, что если состояния S и t различаются некоторой цепочкой, то хотя бы одно из этих условий должно быть нарушено. Если их различает пустая цепочка, то не выполняется условие подобия. (|| =0) Если длинна различающей цепочки > 0, то её первый символ переводит S и t в пару состояний, которые не эквивалентны, т.е. различаются оставшиеся частью цепочки, различающей S и t.

Таким образом, мы видим, что оба условия выполняются если 2 состояния эквивалентны, и что хотя бы одно из них нарушается в случае неэквивалентности состояний.

Условия 1 и 2 можно использовать в общем методе проверки на эквивалентность произвольной пары состояний(или метод поиска различающей цепочки). Рассмотрим на примере, прежде чем сформировать правила проверки в общем виде.

Дата добавления: 2014-01-11