Недостижимые состояния

Пример

	y	z

Для записи необходимых данных мы будем строить таблицы нового типа, которых назовём таблицами эквивалентности состояний.

Сначала мы проверим на эквивалентность состояний 0 и 7.

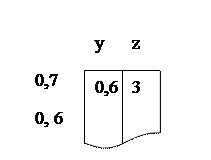
Таблица эквивалентности состояний для этой проверки содержит по одному столбцу для каждого входного символа (y и z). Строки будут добавляться в ходе проверки. Первоначально имеется 1 строка, которая помечена парой состояний подвергаемых проверке (0, 7).

Первым проверяем условие подобия – оно выполняется, т.к. оба состояния являются отвергающими.

Вторым проверяем условие преемственности. Рассмотрим как действует на данную пару состояний каждый входной символ и результат запишем в соответствующую таблицы.

Чтобы нарушилось условие преемственности, должны быть неэквивалентными либо состояния 0 и 6 либо состояния 3 и 3(рефлексия). Теперь, чтобы исследовать на эквивалентность состояния 0 и 6, добавляем в таблицу эквивалентности состояний новую строку, намечаем её этой парой.

Процесс повторяется с новой строки. Обнаруживаем, что 0 и 6 не эквивалентны, т.к. 6 – допускающее, а 0 – отвергающее состояния. => и состояния 0 и 7 не эквивалентны. Таблицу эквивалентности состояния можно использовать для построения различающей цепочки. Строка 0, 6 появилась как результат применения входного символа у к паре 0, 7, поэтому у – различающая цепочка.

Теперь проверяем состояния 0 и 1. Начнем построение таблицы эквивалентности. Эти состояния подобны.

y z y z y z y z

0, 1 | | | - подобны 0, 1 | 0,2 |3,5 | 0, 1 | 0,2 |3,5 | 0, 1 | 0,2 |3,5 |

0, 2 | 0,2 |3,7 | - подобны 0, 2 | 0,2 |3,7 |

3, 5 | | | 3, 5 |6 | 5,7 |

3, 7 | | |

y z

0, 1 | 0,2 |3,5 |

0, 2 | 0,2 |3,7 |

3, 5 |6 | 5,7 |

3, 7 | 6 | 3,7 | - подобны

5, 7 | 6 | 3,5 | - подобны

Таблица заполнена и поиск различающей цепочки окончился неудачей => состояния 0 и 1 ~=> 0,2; 3,5; 3,7; 5; 7; 0,1; ~0,1; 0,2 ~=> 0~1~2.

Среди состояний автомата могут быть такие, которые не достижимы из начального состояния ни для какой входной цепочки, например, таковым состояниям является S4, т.к. в таблице нет перехода в S4.

S0 S1 S2 S3 S4 S5 S6 S7 S8	S1 S2 S2 S5 S5 S3 S8 S0 S3	S5 S7 S5 S7 S6 S1 S0 S1 S6

Такие состояния называют недостижимыми и соответствующие им строки можно удалить.

S0 S1 S2 S3 S5 S6 S7 S8	S1 S2 S2 S5 S3 S8 S0 S3	S5 S7 S5 S7 S1 S0 S1 S6

Дата добавления: 2014-01-11