Корпускулярная природа света

Экспериментальные законы теплового излучения (законы Стефана-Больцмана и Вина)

Закон Кирхгофа, задача физики теплового излучения

Опыт показывает, что между испускательной и поглощательной способностью тел имеется определённая связь. Предположим, что несколько тел A ₁, A ₂ и A ₃ (рис.1) помещены внутрь оболочки C, поддерживаемой при постоянной температуре Т. Пусть внутри оболочки пустота, так что тела могут обмениваться энергией с оболочкой и между собой лишь путём испускания и поглощения света. Опыт показывает, что такая система тел через некоторое время придёт в тепловое равновесие, то есть все тела примут одну и ту же температуру T, равную температуре оболочки. Однако тело, обладающее большей энергетической светимостью R, теряет в единицу времени с единицы площади больше энергии, чем тело, обладающее меньшей светимостью. Отсюда следует, что оно может находиться при постоянной температуре T, одинаковой с температурой других тел, только в том случае, если оно и больше поглощает. Таким образом, из возможности термодинамического равновесия тел, обменивающихся энергией лишь путём излучения и поглощения, вытекает необходимость пропорциональности между испускательной и поглощательной способностями тел. Кирхгоф показал, что эта пропорциональность должна выполняться для каждого интервала длин волн в отдельности. Если тела A ₁, A ₂ и A ₃ характеризуются соответственно испускательными и поглощательными способностями r_{λ 1}, r_{λ 2}, r_{λ 3} и α_{λ 1}, α_{λ 2}, α_{λ 3}, то

.

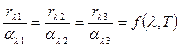(2.11)

Соотношение (2.11) выражает закон Кирхгофа: отношение испускательной способности к поглощательной способности r_λ / α_λ не зависит от природы тела, оно является для тел одной и той же функцией f (λ, T) от длины волны λ и температуры T. В общем случае можем записать

.

(2.12)

Тогда для абсолютно чёрного тела, у которого a_λ =1, закон Кирхгофа сводится к выражению

,

(2.13)

то есть его испускательная способность r_λ выражается непосредственно через f (λ, T). А так как по определению испускательная способность r_λ есть функция распределения светимости по длинам волн, то, следовательно, из последнего соотношения мы получаем, что все абсолютно чёрные тела при данной температуре обладают одним и тем же распределением излучаемой энергии по длинам волн; светимость всех абсолютно чёрных тел одинаково меняется с температурой.

Рисунок 1 – Пример системы трёх тел (A ₁, A ₂, A ₃) находящихся в оболочке S при некоторой температуре T

В природе не существует тел, совпадающих по своим свойствам с абсолютно чёрным телом. Тела, покрытые слоем сажи или платиновой черни, имеют поглощательную способность α_λ, близкую к единице лишь в ограниченном интервале длин волн; в далёкой инфракрасной области их поглощательная способность меньше единицы. Моделью абсолютно чёрного тела может служить почти замкнутый сосуд (рис.2), имеющий небольшое отверстие. Свет, попадая внутрь сосуда через данное отверстие, претерпевает многократные отражения от его стенок, в результате которых практически полностью поглотится, и лишь ничтожно малая часть лучей выйдет обратно. Поэтому поглощательная способность сосуда для всех длин волн будет близка к единице.

Рисунок 2 – Модель абсолютно чёрного тела (почти замкнутый сосуд с отверстием, куда попадает свет)

Простым примером указанной модели могут служить раскрытые окна домов, рассматриваемые с улицы. Так как размеры окон обычно малы по сравнению с размерами комнаты, то даже при хорошем отражении света от стен комнаты обратно из окон на улицу выходит лишь небольшая часть падающего на них светового потока. Поэтому окна кажутся чёрными, независимо от того, какого цвета стены внутри.

По закону Кирхгофа светимость поверхности, для которой α_λ близка к единице, близка в светимости абсолютно чёрного тела. Таким образом, если стенки сосуда (рис.2) находятся при некоторой температуре T, то из отверстия сосуда выходит излучение, весьма близкое к излучению абсолютно чёрного тела при той же температуры T.

Распределение светимости абсолютно чёрного тела по длинам волн хорошо изучено. При данной температуре T зависимость испускательной способности r_λ от длины волны имеет вид, представленный на рисунке 3 (разные кривые относятся к разным температурам). Как видно, излучательная способность тела быстро возрастает с температурой. Каждая кривая имеет один максимум, который при возрастании температуры смещается в сторону коротких длин волн и становится более острым. Вид этих кривых объясняет хорошо известный факт, что светимость, а, следовательно, и яркость тел быстро возрастает с повышением температуры, и что одновременно с этим меняется и цвет испускаемого света. При низкой температуре максимум излучательной способности лежит в области больших длин волн, и тело испускает преимущественно инфракрасные лучи. Доля мощности, приходящейся на видимые лучи, при этом так мала, что глаз не воспримет света. Таков состав излучения при температурах порядка нескольких сот градусов. При температуре около 600°C мощность, приходящаяся на длинноволновый край видимого спектра, окажется достаточной, чтобы вызвать зрительное ощущение, и тело представится светящимся тёмно-красным цветом. При дальнейшем возрастании температуры максимум всё больше и больше смещается в сторону коротких волн, доля мощности, приходящейся на видимые лучи, возрастает, и свечение представляется всё более и более белым.

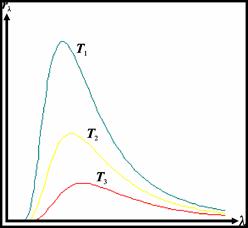
Рисунок 3 – Кривые зависимости испускательной способности r_λ от длины волны λ при разных температурах T, при этом T ₁> T ₂> T ₃

Из сказанного следует, что характер свечения абсолютно чёрного тела однозначно определяется его температурой. Излучательная способность r_λ абсолютно чёрного тела есть определённая функция от длины волны λ и температуры T: r_λ = f (λ, T). Чисто термодинамические рассуждения не дают возможности найти вида этой функции, поэтому задача физики теплового заключалась именно в установлении аналитического вида функции Кирхгофа для абсолютно чёрного тела.

Хотя только лишь термодинамические рассуждения не позволяют найти аналитический вид зависимости излучательной способности абсолютно чёрного тела от длины волны и температуры, они могут быть использованы для установления ряда общих законов теплового излучения. Таких законов три. Первый относится к интегральной светимости: интегральная энергетическая светимость абсолютно чёрного тела R возрастает пропорционально четвёртой степени абсолютной температуры тела T:

,

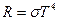(2.14)

где σ =5,67·10^–8 Вт/(м²·К⁴) – постоянная Стефана-Больцмана, значение которой установлено экспериментально, а закон носит название закона Стефана-Больцмана. Так как интегральная светимость связана с испускательной способностью соотношением (2.7), то закон Стефана-Больцмана можно записать в виде

.

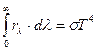(2.15)

Следовательно, интегральная светимость может быть определена как площадь (рис.3) под кривой распределения излучательной способности.

Второй закон касается положения максимума кривых распределения (рис.3). По этому закону, носящему название закона смещения Вина, длина волны λ _max, на которую приходится максимум излучательной способности, меняется обратно пропорционально абсолютной температуры:

,

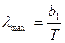(2.16)

где b ₁=2,9·10^–3 м·К – постоянная в законе смещения Вина.

Чем выше температура абсолютно чёрного тела, тем на более короткую длину волны приходится максимум излучательной способности. Из выражения (2.14) видно, что при практически достижимых температурах длина волны, на которую приходится максимум излучательной способности абсолютно чёрного тела, лежит в инфракрасной области. При температуре в 3000 К максимум излучательной способности лежит ещё за пределами видимого спектра. Только при температуре в 5000 К максимум попадает в жёлто-зелёную часть спектра. При температурах выше 7200 К максимум попадает в ультрафиолетовую область.

Третий закон (второй закон Вина) указывает, что максимальная излучательная способность абсолютно чёрного тела (r_λ)_max возрастает пропорционально пятой степени абсолютной температуры:

,

(2.17)

где b ₂=1,3·10^–5 Вт/(м·К) – постоянная во втором законе Вина.

Рисунок 4 – Положение максимума испускательной способности

6. Распределение испускательной способности абсолютно чёрного тела по длинам волн (формулы Рэлея-Джинса и Планка)

Первую попытку найти аналитический вид функции (2.13), удовлетворяющей экспериментальным кривым, сделал московский физик В.А. Михельсон. Однако найденный им вид функции не удовлетворял термодинамическим законам, представленным в предыдущем разделе.

Рэлей и Джинс сделали попытку определить вид функции (2.13), исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT – одна половинка на электрическую энергию, вторая – на магнитную энергию волны. Напомним, что по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равна двум половинкам kT, где k – постоянная Больцмана, T – температура. Таким образом, не вдаваясь в детали, отметим, что ими была получена зависимость r_λ = f (λ, T), которую можно представить в виде:

.

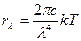(2.18)

Полученное выражение называется формулой Рэлея-Джинса и описывает зависимость испускательной способности абсолютно чёрного тела от температуры и длин волн электромагнитного излучения.

При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты – f (ν, T). В экспериментальных работах удобнее пользоваться функцией длины волны – f (λ, T). Обе функции связаны друг с другом формулой

.

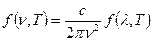(2.19)

Следовательно, вспоминая формулу (1.4) предыдущей лекции, выражение (2.18) может быть представлено как

(2.20)

или с учётом также выражения (1.1) предыдущей лекции запишем

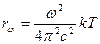
(2.21)

Полученные выражения (2.20) и (2.21) описывают зависимость испускательной способности абсолютно чёрного тела от температуры и частот электромагнитного излучения по теории Рэлея-Джинса.

Формула Рэлея-Джинса удовлетворительно согласуется с экспериментальными данными лишь при больших длинах волн, и резко расходится с опытом для малых длин волн (рис.5). При этом легко видеть, что она приводит к абсурдному результату: энергетическая светимость абсолютно чёрного тела оказывается равной бесконечности:

.

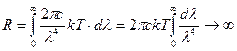(2.22)

Этот результат, получивший название ультрафиолетовой катастрофы, находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливаются при конечных значениях равновесной плотности энергии излучения, а, согласно (2.22), оно наступает только при бесконечно больших значениях.

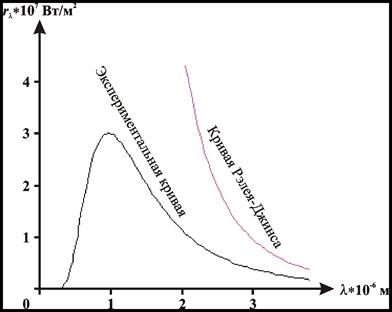
Рисунок 5 – Экспериментальная кривая и кривая формулы Рэлея-Джинса испускательной способности абсолютно чёрного тела при T =298 К

Стоит также отметить, что кривая распределения светимости абсолютно чёрного тела по длинам волн, соответствующая формуле Рэлея-Джинса, даёт монотонное и быстрое возрастание с убыванием длины волны, а на самом деле данное распределение светимости по спектру имеет колоколообразный вид.

Вывод формулы Рэлея-Джинса с классической точки зрения является безупречным. Поэтому расхождение этой формулы с экспериментальными данными указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики и электродинамики.

В 1900 году Максу Планку удалось найти вид функции (2.13), в точности соответствующий результатам опытов. Для этого ему пришлось сделать предположение, совершенно чуждое классическим представлениям, а именно допустить, что электромагнитное излучение испускается в виде отдельных порций энергии ε (квантов), величина которых пропорциональна частоте излучения:

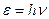
(2.23)

или с учётом выражения (1.4) предыдущей лекции

,

(2.24)

где коэффициент пропорциональности h =6,63·10^–34 Дж·c получил впоследствии название постоянной Планка. Иногда данную величину называют квантом действия, поскольку в механике имеется величина, называемая действием, которая имеет ту же размерность.

Если энергия испускается порциями ε, то полная энергия излучения E должна быть кратна этой величине:

,

(2.25)

где n =1,2,3,… – число квантов электромагнитного излучения.

Не вдаваясь в детали вычислений, запишем зависимость r_λ = f (λ, T), полученную Планком, в виде

.

(2.26)

Полученное выражение может быть переписано, следуя логике получения формул (2.20) и (2.21), в виде

(2.27)

или

,

(2.28)

где ħ – постоянная Планка со штрихом:

.

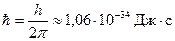(2.29)

Формула, полученная Планком, прекрасно удовлетворяет экспериментальным значениям светимости абсолютно чёрного тела во всей области спектра. Поэтому именно её можно считать решением задачи теплового излучения, поставленной Кирхгофом, и выраженной формулой (2.13).

Также следует отметить, что все экспериментальные законы теплового излучения, приведённые в предыдущем разделе, могут быть получены из формулы Планка. Так, например, для энергетической светимости абсолютно чёрного тела получаем

.

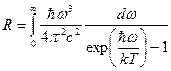(2.30)

Введя вместо ω безразмерную величину x:

,

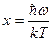(2.31)

и делая подстановку

(2.32)

и

,

(2.33)

из выражения (2.30) получаем

.

(2.34)

Определённый интеграл в приведённом выражении может быть вычислен и равен π ⁴/15. Следовательно,

.

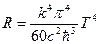(2.35)

Таким образом, мы получаем закон Стефана-Больцмана. Расчёт константы перед температурой в чётвертой степени даёт в точности σ – постоянную Стефана-Больцмана.

Выражения законов Вина предлагается получить из формулы Планка самостоятельно.

1. Фотоэлектрический эффект

2. Тормозное рентгеновское излучение.

3. Опыт Боте.

4. Фотоны (корпускулярные свойства света).

5. Корпускулярно-волновой дуализм.

6. Эффект Комптона.

1. Определение и основные характеристики фотоэффекта

Фотоэлектрическим эффектом, или фотоэффектом, называется испускание электронов вещества под действием света.

Схема установки для изучения фотоэффекта.

Вольтамперная характеристика фотоэлемента.

Экспериментальные законы фотоэлектрического эффекта.

1. Фототок насыщения пропорционален падающему световому потоку (при одном и том же спектральном составе). Это означает, что число электронов, вырываемых светом ежесекундно, пропорционально мощности падающего света.

2. Для каждого металла существует максимальная длина волны λ _К (или минимальная частота ω _К), при которой ещё происходит вырывание электронов. Если длина волны превышает λ _К, так называемую красную границу фотоэффекта, то испускание электронов отсутствует даже при достаточно большой интенсивности света.

3. Максимальная кинетическая энергия K фотоэлектронов линейно зависит от частоты ω облучающего света (причём K _max растёт с увеличением ω) и не зависит от интенсивности света. Отметим, что максимальное значение кинетической энергии фотоэлектронов определяют по так называемой задерживающей разности потенциалов.

Формула Эйнштейна.

Полученная электроном энергия hν частично затрачивается на освобождение из металла. А остальная часть переходит в кинетическую энергию вылетевшего из металла фотоэлектрона. Минимальную энергию, необходимую для освобождения электрона из металла, то есть для преодоления потенциального барьера, называют работой выхода A. Следовательно, для фотоэлектронов с максимальной кинетической энергией K _max закон сохранения энергии в элементарном акте поглощения фотона можно записать, как

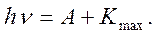Эта формула впервые была получена Эйнштейном и носит его имя – формула Эйнштейна.

1. Максимальная кинетическая энергия фотоэлектронов линейно зависит от частоты падающего света и не зависит от его интенсивности. Интенсивность обусловливает только количество фотоэлектронов, но совершенно не влияет на их максимальную кинетическую энергию.

2. Существует низкочастотная граница – порог фотоэффекта, то есть такая частота ω ₀, ниже которой фотоэффект отсутствует. Это частота согласно формуле Эйнштейна соответствует равенству: A = ħω ₀. Если ω < ω ₀, то энергии фотона не хватает, чтобы электрон мог преодолеть потенциальный барьер высотой A и выбраться из металла.

Дата добавления: 2014-01-11