Изучает закономерности аномалий развития в детском возрасте с психологической точки зрения

Лекция

.

Получаем b + 2 c = 0. Возьмем с =1, тогда b =-2, а из второго уравнения системы имеем a =1. Подставляя найденные значения a, b, c в уравнение плоскости, получаем x - 2 y + z = 0.

Пример 4.24. Найти проекцию точки М (3; 1; -1) на плоскость x + 2 y + 3 z -30 = 0. (рис. 4.9)

М(x,y) – точка вне плоскости; L – прямая, проходящая через точку М перпендикулярно плоскости Р; M₀ - проекция M₁ на плоскость Р, точка пересечения прямой L и плоскости Р; L ₁ N – наклонная плоскости Р; N – точка ее пересечения с плоскостью Р; L ₂ N – проекция наклонной L ₁ N на плоскость Р.  

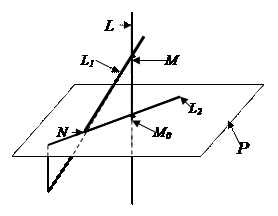
Рис. 4.9. Проектирование точки и прямой на плоскость

Решение. Нужно найти координаты точки М ₀, т.е. основание перпендикуляра, опущенного из точки М на плоскость Р. Составим параметрические уравнения прямой L (по условию L ┴ P.). Для этого возьмем 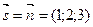и используем координаты точки М.

Получаем x = t + 3, y = 2 t + 1, z = 3 t – 1.

Решая систему

получаем t + 3 + 4 t + 2 + 9 t – 3 – 30 = 0, 14 t = 28, t = 2.

Тогда x = 2 + 3 = 5, y = 2 · 2 + 1 = 5, z = 3 · 2 – 1 = 5, т. е. М ₀(5; 5; 5).

Пример 4.25. Найти уравнение проекции прямой

на плоскость 2 x + 3 y – 4 z – 5 = 0.

Решение. Данная прямая проходит через точку М ₀(1,-2,2) и 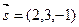- ее направляющий вектор. Плоскость, проектирующая данную прямую на данную плоскость, проходит через точку М ₀ и имеет нормаль 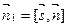, где 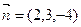- нормаль данной плоскости.

Находим: 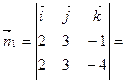(-12+3, 8-2, 0) = (-9, 6, 0).

Уравнение проектирующей плоскости:

-9(x -1) +6(y +2) + 0(z -2) = 0,

9 x – 6 y + 21 = 0, 3 x – 2 y + 7 = 0.

Проекция данной прямой на данную плоскость является пересечением проектирующей плоскости с данной плоскостью. Следовательно, ее уравнение имеет вид

.

Пример 4.26. Найти угол между прямой и плоскостью .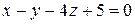

Решение. Направляющий вектор прямой 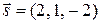, вектор нормали к плоскости 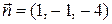. Поэтому

.

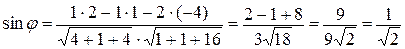Следовательно, угол между прямой и плоскостью .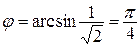

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Головина Л.И. Линейная алгебра и некоторые ее приложения / Л.И.Головина. – М.: Наука, 1985. – 324 с.

2. Грисенко М.В. Математика для економістів: Навчальний посібник. – К.: Видавничо-поліграфічний центр „Київський університет”, 2005. – 586 с.

3. Данко П. Е. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Высш. шк., 1986. – Ч. 1. – 304 с.

4. Калихман И. Л. Линейная алгебра и программирование / И. Л. Ка-лихман. – М.: Высш. шк., 1967. – 188 с.

5. Михайленко В.Г., Матряшин Н.П. Линейная алгебра. Учебный материал. – Х: ХГУ, 1993. – 140 с.

6. Михайленко В.Г., Свіщова Є.В. Лінійна алгебра. Учбові завдання та методичні вказівки для студентів економічних спеціальностей.

7. Травкін Ю.І. Лінійна алгебра і аналітична геометрія: Навчальний посібник. – Х.: Майдан, 2009. – 416 с. Укр. мова.

8. Сенченко Д.В., Слепак Б.Э., Черемных Ю.Н. Высшая математика. Линейная алгебра: Метод. указания для студентов-заочников эконом. фак. гос. ун-тов. –М.: Изд-во Моск. ун-та. 1987. – 67 с.

9. Тевяшев А.Д. Высшая математика. Общий курс: Сб. задач и упражнений / А.Д.Тевяшев, О.Г.Литвин. – Х.: Рубикон, 1999. – 320 с.

Создал это направление В.В.Лебединский.

Основная литература:

Лебединский В.В. «Нарушения психического развития в детском и подростковом возрасте».

Психология аномального развития ребенка. Иногда называют – детская патопсихология.

Психология аномального развития ребенка междисциплинарна. Детская патопсихология напрямую связана с детской психиатрией, с дефектологией, с детской неврологией.

Главный тезис и подход Лебединского, который опирался в первую очередь на идеи Выготского, Бернштейна и Лурии о системности, о структуре диагностики в детском возрасте. Выготский первый обратил внимание на нелинейность диагностики, есть определенная иерархичность, выделил первичные, вторичные и т.д. симптомы нарушения развития, показал их различную природу. Поэтому эти все идеи с одной стороны психологов, с другой стороны идеи детской психиатрии, физиологии и неврологии легли в основу построения фундаментальной классификации типов дизонтогенеза. Прежде чем создать типологию дизонтогенеза, Лебединский выстроил принципы, подходы к диагностике аномального детского развития.

Вплоть до начала 19 в. Не было разделения на детскую и взрослую психиатрию, была общая психиатрия. Считалось, что у детей не может быть психозов. До 19 в. дефектология опережала психиатрию и психологию, в основном дети были очень тяжелые, с грубыми нарушениями, содержались в домах призрения при монастырях, с ними ничего не делалось, не стоял вопрос ни об обучении, ни о воспитании.

Начало развития детской патопсихологией связывают с Францией. Кафедра клинической психологии Сорбонны: Бине, Симон. 1 этап развития детской патопсихологии связан с этими именами. Он решал единственную задачу – диагностики актуального развития. Этот этап связан с идеями французской революции – больной тоже человек, его надо как-то встраивать в этот мир, заниматься его адаптацией. Лозунг: «Прочь цепи с психически больных!». В начале 20 в во Франции ввели всеобщее начальное обучение. И встал вопрос: какие дети могут учиться в школе, а какие нет. Поэтому первый этап развития нашей науки решал одну задачу – диагностика актуального развития. Бине и Симон придумали первую шкалу интеллектуального развития – IQ. Шел грубый отсев «кто может/не может учиться» на основании количественных показателей. И до сих пор: норма – то, что >90, умственная отсталость – то, что <70. Эти дети сразу отсекались, попадали в дома призрения, предполагалось, что они не могут обучаться. Эта диагностика была очень грубая. Потому что низкий интеллектуальный показатель мог дать больной шизофренией незамотивированный, мог дать психопат. Только количественный результат. Большой отряд детей попадал в этот люфт, и все поняли, что маловато заниматься только диагностикой актуального развития и опираться только на количественный показатель.

Дата добавления: 2014-01-11