
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формы остаточного члена в формуле Тейлора
|
|
|
|
Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений.
Лекция 21.
Рассмотрим функцию y=f(x), имеющую в окрестности точки х=а все производные до порядка (n+ 1) включительно, и поставим задачу: найти многочлен y=Pn(x) степени не выше n, для которого его значение в точке а, а также значения его производных по n -й порядок равны значениям при x=a выбранной функции и ее производных соответствующего порядка:
 (21.1)
(21.1)
Пусть искомый многочлен имеет вид:
Pn(x)=C0+C1(x-a)+C2(x-a)²+…+Cn(x-a)n. (21.2)
При этом

Тогда
 (21.3)
(21.3)
Из формул (21.3) можно выразить коэффициенты Сi через значения производных данной функции в точке а.
Замечание. Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n -1) n называется факториалом числа n и обозначается
n! = 1∙2∙3∙…∙(n -1) n. (21.4)
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
 (21.5)
(21.5)
Таким образом, искомый многочлен имеет вид:
 (21.6)
(21.6)
Обозначим через Rn(x) разность значений данной функции f(x) и построенного многочлена Pn(x): Rn(x) = f(x) – Pn(x), откуда f(x) = Pn(x) + Rn(x) или
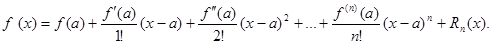 (21.7)
(21.7)
Полученное представление функции называется формулой Тейлора, а Rn(x) называется остаточным членом формулы Тейлора. Для тех значений х, для которых Rn(x) мало, многочлен Pn(x) дает приближенное представление функции f(x). Следовательно, формула (21.7) дает возможность заменить функцию y = f(x) многочленом y = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
Покажем, что Rn(x) = o(x-a)n. Из выбора многочлена Pn(x) следует, что
 Применив для вычисления предела
Применив для вычисления предела  n раз правило Лопиталя, получим:
n раз правило Лопиталя, получим:
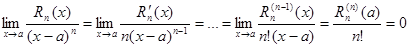 . Утверждение доказано. Представление остаточного члена в виде Rn = o(x-a)n (21.8)
. Утверждение доказано. Представление остаточного члена в виде Rn = o(x-a)n (21.8)
называется записью остаточного члена в форме Пеано.
Найдем еще один вид записи Rn(x). Представим его в виде
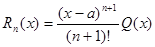 (21.9)
(21.9)
и определим вид функции Q(x). Из (21.7) следует, что

 . (21.10)
. (21.10)
Пусть при заданных значениях х и а Q(x)=Q. Рассмотрим вспомогательную функцию от t (a < t < x):

При этом предполагается, что а и х приняли фиксированные значения. Тогда
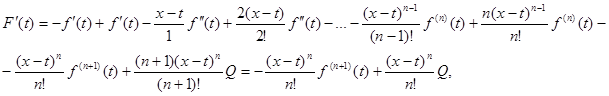
то есть F(t) дифференцируема в окрестности точки а. Из (21.10) следует, что F(x) = F(a) = 0, поэтому к функции F(t) можно применить теорему Ролля: существует t = ξ (a < ξ < x) такое, что F′(ξ) = 0. Тогда  , откуда Q = f(n+1) (ξ). Подставив это выражение в формулу (21.9), получим запись остаточного члена в форме Лагранжа:
, откуда Q = f(n+1) (ξ). Подставив это выражение в формулу (21.9), получим запись остаточного члена в форме Лагранжа:
 .
.  (21.11)
(21.11)
Так как a < ξ < x, можно представить ξ = а + θ(х – а), где 0 < θ < 1. При этом
 . (21.12)
. (21.12)
Замечание. Если в формуле Тейлора принять а = 0, этот частный случай называют формулой Маклорена:
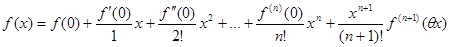 . (21.13)
. (21.13)
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 628; Нарушение авторских прав?; Мы поможем в написании вашей работы!