Асимптоты. Определение 23.4. Прямая называется асимптотойграфика функции y = f(x) , если расстояние от переменой точки этого графика до прямой стремится к нулю при

Определение 23.4. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность.

Рассмотрим три вида асимптот и определим способы их нахождения.

1. Вертикальные асимптоты – прямые, задаваемые уравнениями вида х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен. Пример. Вертикальной асимптотой графика функции y = 1/ x является прямая х = 0, то есть ось ординат.

2. Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при или при конечен, т.е. .

3. Наклонные асимптоты – прямые вида y = kx + b. Найдем k и b. Поскольку при 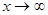, , если этот предел существует, конечен и не равен нулю. Однако даже при выполнении этих условий наклонная асимптота может не существовать. Для ее существования требуется, чтобы имелся конечный предел при 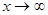разности f(x) – kx. Этот предел будет равен b, так как при .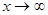

Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при и при ).

Примеры.

1. Функция y = tg x имеет разрывы 2-го рода при 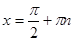, причем односторонние пределы в этих точках бесконечны. Следовательно, 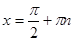- вертикальные асимптоты графика.

2. Функция 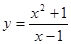имеет бесконечный разрыв при х = 1, то есть х = 1 – вертикальная асимптота. 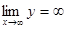, поэтому горизонтальных асимптот график не имеет. Проверим наличие наклонных асимптот. Для этого вычислим 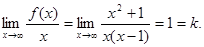Тогда Заметим, что оба предела не зависят от знака бесконечности, поэтому прямая y = x + 1 является асимптотой графика на обоих концах оси Ox.

Общая схема исследования функции.

Результаты, полученные при изучении различных аспектов поведения функции, позволяют сформулировать общую схему ее исследования с целью построения качественного графика, отражающего характерные особенности поведения данной функции. Для этого требуется определить:

1) область определения функции и ее поведение на границах области определения (найти соответствующие односторонние пределы или пределы на бесконечности);

2) четность и периодичность функции;

3) интервалы непрерывности и точки разрыва (указав при этом тип разрыва);

4) нули функции (т.е. значения х, при которых f(x) = 0) и области постоянства знака;

5) интервалы монотонности и экстремумы;

6) интервалы выпуклости и вогнутости и точки перегиба;

7) асимптоты графика функции.

Заметим, что подробный ответ на первый вопрос фактически содержит ответы на второй и отчасти на седьмой вопросы. Действительно, если в область определения не входят отдельно расположенные точки и найдены односторонние пределы функции в этих точках, то тем самым указан характер разрывов. В частности, если какой-либо из этих односторонних пределов бесконечен, через точку разрыва (или через соответствующую границу области определения) проходит вертикальная асимптота. Если область определения функции не ограничена слева или справа и на бесконечности соответствующего знака существует конечный предел функции, то график имеет на указанном конце оси Ох горизонтальную асимптоту.

Пример. Исследуем функцию 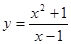и построим ее график.

1. Область определения функции: 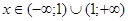. Поведение на границах: .

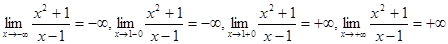2. 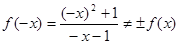, следовательно, функция не является четной или нечетной (в этом случае говорят, что рассматриваемая функция общего типа). Функция не является периодической, так как периодическая функция, не равная константе, не может иметь предела на бесконечности.

3. Так как функция является элементарной, она непрерывна во всей области определения, т.е. промежутки непрерывности 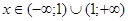. Из ответа на первый вопрос следует, что х = 1 – точка разрыва 2-го рода (так как односторонние пределы в этой точке бесконечны).

4. 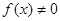ни при каких значениях х (следовательно, график функции не пересекает ось Ох). f(x) < 0 при х < 1, f(x) > 0 при x > 1.

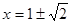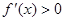5. Для ответа на этот вопрос найдем производную данной функции. при . при - интервалы убывания функции; при 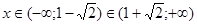- интервалы возрастания функции. При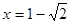 меняет знак с «+» на «-», следовательно, 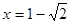- точка максимума. При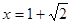 меняет знак с «-» на «+», следовательно, 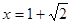- точка минимума.

6. ни при каких значениях х. Следовательно, функция не имеет точек перегиба. при х < 1, 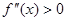при x > 1, поэтому на интервале 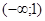функция выпукла, а на интервале - вогнута.

7. При ответе на первый вопрос показано, что х = 1 – вертикальная асимптота графика функции. Там же выяснено, что при 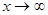функция не имеет конечного предела, следовательно, не имеет и горизонтальных асимптот. Наклонная асимптота у = х + 1 найдена в примере 2 настоящей лекции.

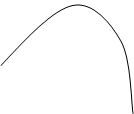
Построим график функции 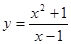на основе результатов проведенного исследования.

у

1-√2 1 1+√2 х

Дата добавления: 2014-01-11