Необходимое условие экстремума

Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке.

Лекция 22.

В предыдущих лекциях использовались известные из курса элементарной математики понятия возрастающей и убывающей функций. Определим их еще раз.

Определение 22.1. Функция y = f(x) называется возрастающей (убывающей) на [ ab ], если

таких, что x₁ < x₂, f(x₁) < f(x₂) (f(x₁) > f(x₂)).

Теорема 22.1. Если функция f(x), дифференцируемая на [ ab ], возрастает на этом отрезке, то на [ ab ].

Если f(x) непрерывна на [ ab ] и дифференцируема на (ab), причем 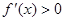для a < x < b, то эта функция возрастает на отрезке [ ab ].

Доказательство.

1. Пусть f(x) возрастает на [ ab ]. Тогда при то есть Если же 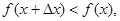поэтому 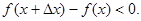Следовательно, в обоих случаях 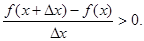Значит, что и требовалось доказать.

1. Пусть 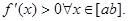Выберем По теореме Лагранжа

Но по условию поэтому f(x₂) > f(x₁), следовательно, f(x) – возрастающая функция.

Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: Если f(x) убывает на [ ab ], то на [ ab ]. Если на (ab), то f(x) убывает на [ ab ].

Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [ ab ], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна). Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох).

В лекции 19 было дано определение максимума и минимума функции.

Теорема 22.2 (необходимое условие экстремума). Пусть функция f(x) задана в некоторой окрестности точки х₀. Если х₀ является точкой экстремума функции, то или не существует.

Доказательство. Действительно, производная в точке х₀ либо существует, либо нет. Если она существует, то по теореме Ферма она равна нулю.

Примеры.

1. Функция y = x ² имеет минимум при х = 0, причем (х ²)′ = 2 x = 0 при х = 0.
2. Минимум функции y = | x | достигается при х = 0, причем производная в этой точке не существует.

Замечание. Отметим еще раз, что теорема 22.2 дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′(x) = 0, функция достигает экстремума.

Пример. У функции y = x ³ y ′ = 3 x ² = 0 при х = 0, однако функция монотонно возрастает во всей области определения.

Определение 22.2. Если функция определена в некоторой окрестности точки х₀ и ее производная в этой точке равна нулю или не существует, точка х₀ называется критической точкой функции. Теорема 22.1 означает, что все точки экстремума находятся в множестве критических точек функции.

Дата добавления: 2014-01-11