Частотные характеристики. Наряду с методом временных характеристик для исследования систем широко пользуются методом частотных характеристик

Наряду с методом временных характеристик для исследования систем широко пользуются методом частотных характеристик, которые также описывают динамику систем при воздействии на их вход гармонических колебаний. Гармонические колебания вида:

(2.86)

являются периодической функцией времени, т.е. они удовлетворяют условию

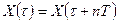(2.87),

где Т – период колебаний,

n – любое целое число.

Отличительной особенностью периодических функций является то обстоятельство, что они существуют от до 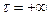С этой точки зрения периодические функции времени являются математической абстракцией, так как всякий реальный процесс имеет начало и конец. Однако, если реальный процесс длится достаточно долго с периодическим повторением предыдущих значений, он может в достаточной для практики точностью считаться периодическим. Таким образом, в реальных условиях реакцией системы на периодические входные воздействия могут считаться только установившееся колебания выходной величины, т.е. колебания, которые возникают в системе по истечении достаточно большого времени после начала подачи входного воздействия. В этом принципиальное отличие метода частотных характеристик от метода временных характеристик: если в методе временных характеристик рассматривают прежде всего поведение системы в переходных процессах, то здесь интересуются только установившимися колебаниями. Несмотря на это, частотные характеристики столь же полно определяют изменение выходной координаты во времени, как и временные характеристики или дифференциальное уравнение.

Частотные характеристики показывают, как через динамическую систему проходят гармонические колебания входного воздействия вида:

,

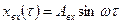имеющие форму синусоидального сигнала с амплитудой А_вх и частотой, определяемой периодом Т

.

Что же мы получим на выходе системы при подаче на вход таких колебаний? Чтобы ответить на поставленный вопрос обратимся к примеру. В качестве исследуемого звена возьмем гидравлический привод. Дифференциальное уравнение этого звена имеет вид:

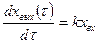(2.88)

Допустим, что на выходе этого звена установились гармонические колебания вида:

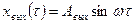(2.89)

Как можно представить, что выход изменяется по такому закону? Выходная величина это перемещение поршня. Если в состоянии равновесия поршень находится в середине цилиндра, то после подачи какого-то воздействия он стал перемещаться сначала в одну сторону, затем достигнув определенной точки, начинает двигаться назад. Пройдя равновесное состояние, от которого он начал движение, поршень пройдет такой же путь, что и в первом случае, и начнет движение в противоположную сторону. Какое же входное воздействие заставляет его так перемещаться? Для того, чтобы найти входную координату, подставим выход в дифференциальное уравнение:

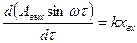(2.90)

Из уравнения (290) получим:

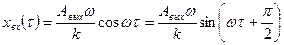(2.91)

Изобразим входные и выходные колебания на графике (рис. 2.17).

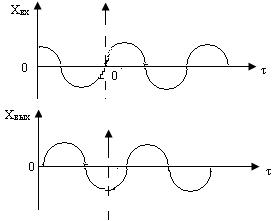
Рисунок 2.17 – Графики колебаний входной и выходной координат

Так как эти колебания совершаются достаточно долго, можно перенести начало координат в точку 0^’. Из рисунка видно, что входные колебания представляют собой синусоиду вида:

(2.92),

а выходные – синусоиду вида:

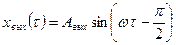(2.93)

Рассмотрим второй пример. Звено описывается дифференциальным уравнением первого порядка (2.82). Допустим, что и в этом случае на выходе установились гармонические колебания вида (2.89). Что было подано на входе определим, подставив уравнение (2.89) в уравнение (2.82):

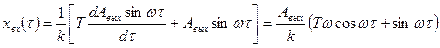(2.94)

В уравнении (2.94) выполним подстановку:

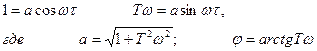(2.95)

Тогда

(2.96)

Или входные и выходные колебания можно представить следующим образом:

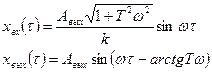(2.97)

Таким образом, из этих примеров видно, что если на вход линейной системы подавать гармонические колебания с частотой ω, то на выходе системы спустя определенное время также установятся гармонические колебания с той же частотой ω, но с другой амплитудой и сдвинутые по фазе относительно входных колебаний.

Найдем отношение амплитуд выходных колебаний к амплитудам входных колебаний:

для первого случая

(2.98)

для второго случая

(2.99)

Как видно из уравнений (2.98) и (2.99), отношение амплитуд является функцией частоты, причем частота может изменяться от 0 до .

Зависимость отношения амплитуд выходных колебаний к амплитудам входных колебаний от частоты называется амплитудно-частотной характеристикой (АЧХ).

Найдем разность фаз между фазой выходных колебаний и фазой входных колебаний. Для первого случая имеем:

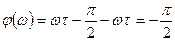(2.100);

для второго случая имеем:

(2.101).

Зависимость разности фаз выходных колебаний и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ).

Эти две характеристики, которые обычно рассматривают совместно, образуют амплитудно-фазовую характеристику (АФХ) системы.

Что же дают эти характеристики? Например, если в результате опыта найдены отношение амплитуд выходных и входных колебаний и сдвиг фаз для определенной частоты, то можно определить параметры исследуемого объекта, которые другими методами иногда не удается определить. Сама амплитудно-фазовая характеристика показывает, как изменяется амплитуда и фаза гармонических колебаний при прохождении их через линейную динамическую систему.

Путь получения АФХ, рассмотренный выше, довольно длителен. Существует довольно простой метод получения АФХ. Общий метод получения АФХ заключается в том, что в передаточную функцию вместо параметра преобразования Лапласа р подставляется , где 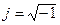, и обозначают её W(jω).

Например, передаточная функция, соответствующая уравнению (2.82), имеет вид:

(2.102).

Подставим в уравнении (2.102) вместо р:

(2.103).

Получили мнимое число, в котором j находится в знаменателе. Обычно же комплексное число записывают в такой форме:

Z=a +jb

Избавимся от мнимости в знаменателе, умножив числить и знаменатель на комплексно-сопряженное число со знаменателем:

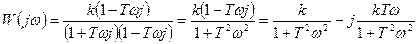(2.104).

Введем обозначения:

Величина Re(ω) называется вещественной частотной характеристикой. Величина Im(ω) называется мнимой частотной характеристикой.

Следовательно, АФХ в общем виде можно записать следующим образом:

W(jω)= Re (ω) + jIm (ω) (2.105)

Однако раньше были получены А(ω) и φ(ω). А какое же отношение к ним имеют Re (ω) и Im (ω)? Вспомним, что комплексное число Re (ω)+j Im (ω) можно записать в комплексно-показательной форме. Построим на комплексной плоскости точку, соответствующую указанному числу (рис. 2.18).

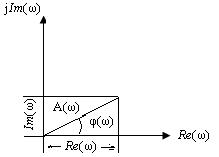
Рисунок 2.18 – Точка на комплексной плоскости

Положение этой точки характеризуется числами Re (ω) и Im (ω).С другой стороны, положение этой точки можно охарактеризовать длиной вектора, соединяющего эту точку с началом координат, и углом, под которым этот вектор проходит относительно оси абсцисс. Из рисунка 2.18 видно, что

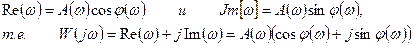(106)

Используя формулу Эйлера

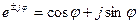(107),

Получим

W(jω)= Re (ω) + jIm (ω)= (2.108),

где

(2.109)

(2.110)

Таким образом, получена связь между АЧХ, ФЧХ, вещественной и мнимой частотными характеристиками.

Можно привести общее правило получения АФХ, если известно дифференциальное уравнение. Если известно дифференциальное уравнение звена или системы, то для получения АФХ необходимо:

- записать дифференциальное уравнение в операторной форме;

- найти передаточную функцию как отношение преобразованной выходной координаты к преобразованной входной координате при нулевых начальных условиях;

- заменить в передаточной функции символ р на jω;

- освободиться от иррациональности в знаменателе;

- записать АФХ в показательной форме.

Для рассмотренного случая АФХ в показательной форме имеет вид:

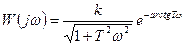(2.111)

Более наглядное представления о характеристиках дают графики. На рисунках 2.19, 2.20 и 2.21 приведены графики АЧХ, ФЧХ и АФХ для звена с передаточной функцией, соответствующей дифференциальному уравнению 2.82.

Рисунок 2.19 – Амплитудно-частотная характеристика

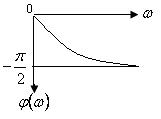
Рисунок 2.20 – Фазо-частотная характеристика

Рисунок 2.21 – Амплитудно-фазовая характеристика

Кривая, приведенная на рисунке 2.21, называется годографом АФХ. Годограф АФХ занимает столько квадрантов, каков порядок дифференциального уравнения.

Дата добавления: 2014-01-11