Интегрирующее звено и его свойства

Интегрирующим называется такое звено, у которого скорость изменения выходной координаты пропорциональна входной координате.

Дифференциальное уравнение этого звена имеет вид:

(3.10)

Уравнение интегрирующего звена можно записать и в таком виде:

(3.11)

Тогда определение звена может быть дано в следующей форме.

Интегрирующим называется такое звено, у которого выходная координата пропорциональна интегралу по времени от входной координаты.

Коэффициент передачи звена 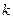имеет размерность

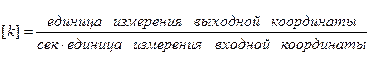
Интегрирующее звено иногда называют астатическим, так как оно не имеет статической характеристики.

Запишем передаточную функцию звена. Для этого запишем уравнение 3.7 в операторном виде при нулевых начальных условиях:

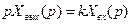
откуда

(3.12)

Переходную функцию звена получим, решив уравнение (3.8) при 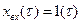и .

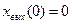(3.13)

Переходная характеристика звена приведена на рисунке 3.4.

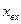
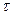
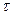
Рисунок 3.4– Переходная характеристика интегрирующего звена

Определим импульсную переходную функцию интегрирующего звена. Для этого необходимо решить уравнение (3.11) при единичном импульсном изменении входной координаты (3.7):

Решение имеет вид:

(3.14)

График импульсной переходной функции приведен на рисунке 3.5

Рисунок 3.5 – Импульсная переходная характеристика интегрирующего звена

Определим частотные характеристики интегрирующего звена, подставив jω вместо р в передаточную функцию:

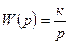(3.15)

, (3.16)

где

(3.17)

Графики амплитудно-частотной, фазо-частотной и амплитудно – фазовой характеристик приведены на рисунках 3.6; 3.7 и 3.8 соответственно.

Рисунок 3.6 – Амплитудно-частотная характеристика интегрирующего звена

Рисунок 3.7 – Фазо-частотная характеристика интегрирующего звена

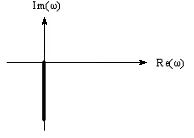
Рисунок 3.8 – Амплитудно-фазовая характеристика интегрирующего звена

К интегрирующим звеньям можно отнести электрический двигатель постоянного тока с независимым возбуждением при условии, что электромеханическая и электромагнитная постоянные времени относительно малы и ими можно пренебречь (входной координатой является напряжение якоря, а выходной – угол поворота вала электродвигателя), поршневой гидравлический исполнительный двигатель при пренебрежении массой и силами трения (входной координатой является скорость подачи жидкости в цилиндр, а выходной – перемещение поршня), бункер с флюсом (входной координатой является расход флюса, а выходной – его уровень в бункере) и др.

Дата добавления: 2014-01-11