Пропорциональное звено и его свойства

Типовые элементарные звенья

Рассматривая динамические характеристики АСР и отдельных элементов, и в частности дифференциальные уравнения, мы смогли убедиться, что совершенно различные по своей конструкции и назначению элементы могут быть описаны вполне идентичными дифференциальными уравнениями, а, следовательно, идентичны и переходные процессы в этих элементах. Чтобы убедиться в этом, достаточно вспомнить дифференциальные уравнения, описывающие динамические свойства электрической цепочки, состоящей из резистора и конденсатора, и термопары или бака с водой при принудительном сливе и электродвигателя. Поэтому при теоретических исследованиях САР существенное значение имеет разделение ее элементов не по конструктивным и функциональным признакам, а по их динамическим свойствам. Это дает возможность разные элементы, имеющие различные принципы действия и конструктивные оформления, описывать одинаковыми дифференциальными уравнениями. Особенно удобно для целей исследования АСР разделение ее на элементы, дифференциальные уравнения которых могут быть нулевого, первого или в крайнем случае второго порядка.

Элементы, которые рассматриваются с точки зрения их динамических свойств и не могут быть различны, называются элементарными типовыми динамическими звеньями. Любая АСР может быть разбита на элементарные звенья, переходные процессы в которых описываются линейными дифференциальными уравнениями не выше второго порядка. Все реальные элементы автоматических систем регулирования можно разбить в основном на шесть групп элементарных динамических звеньев: пропорциональные, интегрирующие, дифференцирующие, инерционные, колебательные и запаздывающие.

Звено называют пропорциональным, если его выходная координата пропорциональна входной, т.е. выход воспроизводит вход без искажений и запаздываний.

Уравнение этого звена записывается так:

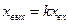, (3. 1 )

где 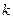– коэффициент передачи звена, имеющий размерность

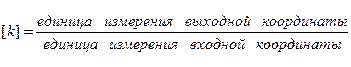
Записанное уравнение звена является статической характеристикой. Дифференциального уравнения это звено не имеет. Поэтому при рассмотрении его динамических свойств необходимо выходную и входную координаты рассматривать как функции времени, т.е. необходимо рассматривать уравнение вида

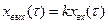(3.2)

Найдем передаточную и переходную функции этого звена.

Для определения передаточной функции преобразуем уравнение (3.2) по Лапласу при нулевых начальных условиях:

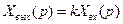(3.3)

Отсюда передаточная функция звена

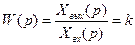(3.4)

Переходная функция, как известно, представляет собой решение уравнения, описывающего динамические свойства звена, при единичном скачкообразном изменении входной координаты, т.е.

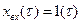(3.5)

Подставив уравнение (3.5) в уравнение (3.3), получим переходную функцию

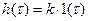(3.6)

Изобразим на графике изменение входной и выходной координат (рис. 3.1). График изменения во времени выходной координаты звена, вызванного подачей на его вход единичного скачка, называется переходной характеристикой или временной характеристикой.

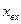
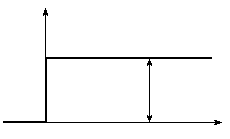
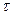
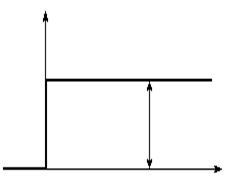
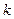
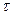
Рисунок 3.1–Переходная характеристика пропорционального звена

Из рисунка видно, что переходный процесс в таком звене отсутствует. В этом звене скачкообразное изменение входной координаты мгновенно передается на выход. Поэтому это звено часто называют безынерционным.

Определим импульсную переходную функцию пропорционального звена. Для этого необходимо решить уравнение (3.2) при единичном импульсном изменении входной координаты:

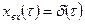(3.7)

Решение имеет вид:

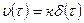(3.8)

График импульсной переходной функции приведен на рисунке 3.2

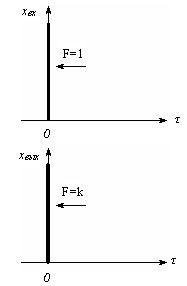
Рисунок 3.2–Импульсная переходная характеристика пропорционального звена

Определим частотные характеристики пропорционального звена, подставив jω вмес-то р в передаточную функцию:

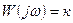(3.9)

График амплитудно – фазовой характеристики приведен на рисунке 3.3.

Рисунок 3.3–Амплитудно – фазовая характеристика пропорционального звена

Примерами безынерционных звеньев являются механический редуктор, потенциометр, механическая пружина, сельсин, трансформатор, жесткий рычаг и др.

Дата добавления: 2014-01-11