Определение формального исчисления

Тема 3. ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ

Широкое использование аксиоматического метода в построении математических теорий стало одной из важных причин появления и развития математической логики. При таком подходе выбирается система основных неопределяемых понятий и отношений между ними, далее, постулируется система свойств основных понятий и отношений, называемых аксиомами. Новые понятия теории вводятся через основные или ранее определенные, а утверждения выводятся из аксиом или из ранее доказанных утверждений.

Всякую математическую теорему можно записать в виде импликации, выделив условие и заключение. При доказательстве теоремы из ее условия по определенным правилам получают заключение, при этом говорят, что заключение является логическим следствием условия или что оно выводимо из условия.

Логическим исчислением принято называть синтаксическую (т.е. формализованную аксиоматическую) теорию математической логики. Описание всякого исчисления I включает:

1) описание алфавита A(I), т.е. множества используемых символов, последовательности которых называются словами исчисления, множество всех слов обозначим W(I);

2) описание языка E(I), т.е. правил построения допустимых последовательностей символов (слов) алфавита, называемых формулами и секвенциями, из W(I) (E(I)ÌW(I));

3) задание системы аксиом Ax(I) – некоторого множества истинных формул, называемых аксиомами (Ax(I)ÍE(I));

4) определение правил вывода R(I), позволяющих из одних истинных формул получать другие формулы рассматриваемой синтаксической теории.

Для записи правил вывода используют сокращенную схему, которая имеет вид

,

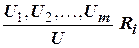и читаются следующим образом. “Если формулы U₁, U₂,..., U_m истинны, то в соответствии с правилом вывода R _i формула U также истинна”.

Таким образом, I = < A(I), E(I), Ax(I), R(I) >.

Указанием аксиом и правил вывода мы полностью определили понятие истинной, или выводимой в формальном исчислении, формулы. Пользуясь правилами вывода, мы можем, исходя из аксиом, конструировать новые истинные формулы и получать, таким образом, каждую истинную формулу.

Формула B называется доказуемой (теоремой формального исчисления), что обозначается |- B, если существует конечная последовательность формул

B₁, B₂,..., B_t = В, (1)

в которой каждая из формул B_i является либо аксиомой, либо, получена по правилам вывода из некоторых предыдущих формул последовательности (1). Эта последовательность называется доказательством формулы (теоремы).

Формула B выводима из формул U₁, U₂,..., U_n, называемых исходными посылками, что записывается символически как

U₁, U₂,..., U_n |- B,

если существует такая конечная последовательность формул (1), что B_t есть B и для каждой формулы B_i выполнено одно из условий:

1) B_i есть посылка или теорема формального исчисления;

2) B_i получена из некоторых предыдущих формул последовательности (1) по правилам вывода.

Последовательность (1) называется в этом случае выводом формулы B из системы посылок U₁, U₂,..., U_n.

Заметим, что если посылки являются аксиомами или теоремами формального исчисления, то класс выводимых из них формул совпадает с классом всех истинных формул, выводимых из любой системы посылок.

Существует два типа формальных исчислений, в основе которых лежат формулы алгебры логики, это исчисления генценовского и гильбертовского типа.

Дата добавления: 2014-01-11