Модель. Формула алгебры предикатов сигнатуры s

Ряд важнейших понятий алгебры предикатов основывается на понятии модели.

Моделью M называется любое множество M с заданными на нем предикатами :

M = < M; >.

Множество M называется основным множеством модели M, предикаты – основными предикатами модели M, и их набор z = <> называется сигнатурой модели M. Натуральные числа k ₁, ¼, k_n обозначают арности соответствующих предикатов, а их набор t = < k ₁, ¼, k_n > называется типом модели.

Пример. Í – множество натуральных чисел, E, S, P – определенные на множестве Í предикаты равенства, сложения и умножения, т.е.

.

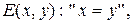
Модель N = < Í; E, S, P > является арифметикой натуральных чисел. Ее сигнатура z = < E, S, P > и тип t = < 2, 3, 3 >.

Любое множество моделей с одной и той же сигнатурой z называется классом K_z моделей сигнатуры z.

Определим формулу алгебры предикатов сигнатуры z. Так же как и в алгебре высказываний, такое определение является индуктивным.

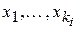1. Если и – предметные переменные, то выражение есть формула. Такая формула называется атомарной, в ней все вхождения предметных переменных называются свободными.

2. Если U есть формула, в которой имеются свободные вхождения переменной x_i, то выражения " x_i (U) и $ x_i (U) – формулы, в которых все вхождения x_i являются связанными, а все вхождения остальных предметных переменных такие же, какими они были в формуле U. При этом формула U называется областью действия соответствующего квантора всеобщности или существования.

3. Если U есть формула, то Ø U – также формула, и все свободные и связанные вхождения предметных переменных в формулу U являются соответственно свободными и связанными вхождениями в формуле Ø U.

4. Если U и V есть формулы, то выражения (U) Ù (V), (U) Ú (V), (U) ® (V), (U) ~ (V) также являются формулами, причем все вхождения предметных переменных в этих формулах такие же, как и в формулах U и V.

5. Формулы могут быть образованы только с помощью правил 1 – 4.

Число скобок в формуле можно уменьшить, если условиться:

- не заключать в скобки атомарные формулы и формулы, над которыми записан знак отрицания;

- вместо записи 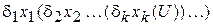, где – некоторые кванторы, допускать запись ;

- не использовать скобки, если порядок выполнения операций соответствует приоритету операций, причем приоритет операций утверждения всеобщности и существования наивысший, для остальных операций такой же, как и в алгебре высказываний;

- не заключать в скобки подформулы, обозначенные буквами;

- не указывать явно с помощью верхнего индекса местность предиката.

Если формула U не содержит свободных вхождений предметных переменных, то, используя определения операций, можно вычислить её логическое значение. Если в формуле U есть свободные вхождения предметных переменных, то она является предикатом, называемым формульным, зависящим от значений этих переменных. Но при каждой замене в этой формуле всех свободных вхождений предметных переменных элементами множества M она становится высказыванием, значение которого вычисляется так же, как и в первом случае.

Например, формула 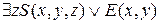на модели арифметики натуральных чисел является формульным предикатом от переменных x и y, т.е.

(1)

и определяет отношение 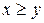. Легко проверить, что , , .

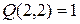Формула называется выполнимой на модели M, если для некоторой системы элементов 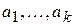модели M сигнатуры z значение формулы сигнатуры z, т.е. высказывание , является истинным.

Формула U сигнатуры z называется выполнимой, если существует модель сигнатуры z, на которой выполнима формула U.

Если высказывание является истинным для любой системы значений 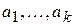Î M, то формула U называется истинной на модели M.

Если формула не выполнима на модели M, то она называется ложной на модели M.

Так формула (1) является выполнимой на модели N, но она не будет ни истинной, ни ложной на ней. Формула

выражает однозначность операции сложения и является истинной на этой модели, а формула – ложной.

Если формула U истинна на любой модели класса K_z, то она называется истинной на классе K_z.

Дата добавления: 2014-01-11