Формулы алгебры предикатов

Так как задача математической логики состоит в описании общих методов умозаключений, то алгебра предикатов должна строиться так, чтобы среди ее символов не было символов, принадлежащих конкретным моделям или классам моделей. Вместо символов предикатов фиксированной сигнатуры в алгебре предикатов используются символы предикатных переменных. Из алгебры предикатов замещением предикатных переменных предикатами сигнатуры s выделяется алгебра предикатов сигнатуры s.

Введем счетное множество предикатных переменных 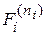, , 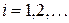счетное множество символов предметных переменных, символы операций и круглые скобки.

Понятие формулы алгебры предикатов определяется также как и формулы алгебры предикатов сигнатуры s. Число всех символов операций, входящих в запись формулы U, называется её рангом и обозначается 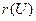. Формула называется атомарной, она может записываться , её ранг = 0.

Формула алгебры предикатов сигнатуры s является или высказыванием или некоторым предикатом на модели M. Формула алгебры предикатов является только определенным образом построенной последовательностью символов. Из одной и той же формулы алгебры предикатов можно образовать различные формулы сигнатуры s и формулы различных сигнатур, после чего можно будет говорить об истинностных значениях формулы алгебры предикатов.

Определение. Пусть U – формула алгебры предикатов и

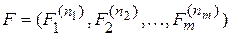(2)

набор предикатных переменных, входящих в U. Сигнатуру s, а также класс моделей K_s и модель M Î K_s назовем допустимыми для формулы U, если s содержит хотя бы один предикат арности n_i для любого , т.е. существует отображение .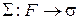

Такое отображение назовем сигнатурным. Формула, полученная заменой каждой предикатной переменной 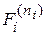её образом S(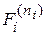), является формулой сигнатуры s и обозначается s U.

Например, для формулы алгебры предикатов

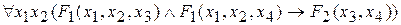
модель арифметики натуральных чисел N = < N; E, S, P > является допустимой, так как можно построить сигнатурное отображение 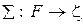множества предикатных переменных формулы 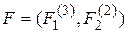в сигнатуру модели z = < E ⁽²⁾, S ⁽³⁾, P ⁽³⁾ >. Вариантов такого отображения два:

1) , ;

2) , .

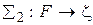Обозначим через s U формулу, полученную подстановкой в формулу U предикатов сигнатурного отображения å.

Определение. Пусть для формулы алгебры предикатов U модель M является допустимой. Тогда:

a) формула U называется выполнимой на модели M, если формула s U выполнима на модели M при некотором сигнатурном отображении S;

b) формула U называется выполнимой, если существует допустимая модель, на которой она выполнима;

c) формула U называется невыполнимой или ложной на модели M, если формула s U невыполнима на модели M при любом сигнатурном отображении S;

d) формула U называется невыполнимой, если на любой допустимой модели она не выполнима;

e) формула U называется тождественно истинной на модели M, если формула s U истинна на модели M при любом сигнатурном отображении S;

f) формула U называется общезначимой, если она тождественно истинна на любой допустимой модели.

Примеры.

Формула алгебры предикатов на допустимой модели арифметики натуральных чисел N = < N; E, S, P > является ложной, так как для любых 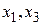не существует такое натуральное x ₂, что 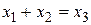или .

Формула алгебры предикатов общезначима.

Дата добавления: 2014-01-11