Метод наименьших квадратов (МНК)

При решении экономических задач часто возникает необходимость представления опытных данных в аналитическом виде. Наиболее известным математическим методом для этих целей является метод наименьших квадратов.

Пусть имеются опытные данные в виде таблицы

	.......
	.......

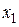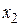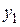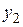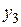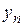
из двух строк, в первой строке которой находятся значения некоторой переменной, принимаемой за независимую, а во второй соответствующие значения другой переменной, принимаемой за функцию. Требуется найти аналитическую функциональную зависимость .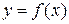

Наиболее просто найти аналитическую зависимость возможно с помощью интерполяционного многочлена Лагранжа, который в общем виде записывается следующим образом

.

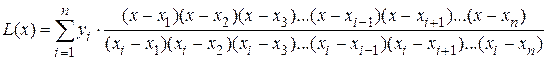График данной функции проходит совершенно точно через заданные точки (рис. 50).

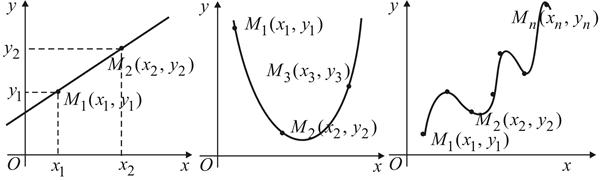
Рис. 50

В случае, если имеются два точки , , 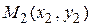то данная формула позволяет написать уравнение прямой, проходящей через эти точки

.

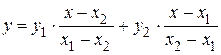В случае, если имеются три точки , , 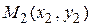, то данная формула позволяет написать уравнение параболы, проходящей через эти точки

.

Если известно n точек, то можно написать уравнение линии, представляющей многочлен (n -1)-ой степени относительно х.

Пример 3.25. Написать уравнение параболы, проходящей через точки .

В соответствии с многочленом Лагранжа записываем

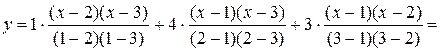
, т. е. .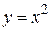

Интерполяционный многочлен Лагранжа позволяет записать уравнение кривой, проходящей через любое число заданных точек. Однако, его удобно использовать при небольшом числе точек. В экономических задачах число точек может быть равным сотням и тысячам. Использование многочленов очень высокого порядка представляет затруднение даже при использовании современных вычислительных устройств. Поэтому при решении экономических задач используют методы аппроксимации.

Аппроксимацией называется нахождение функции заданного вида, обеспечивающей наилучшее приближение к опытным данным.

В методе наименьших квадратов (МНК) качество приближения оценивается по сумме квадратов отклонений значений аппроксимирующей функции 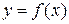от опытных данных i = 1, 2, … (рис. 51), т. е.

.

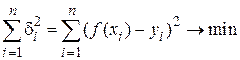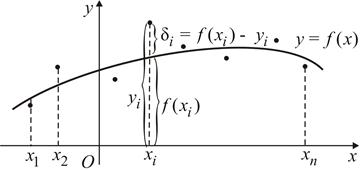
Рис. 51

Функция, по которой оценивается качество аппроксимации, называется критерием качества.

Аппроксимирующую функцию выбирают в зависимости от характера расположения точек опытных данных. Эта функция 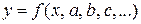обычно имеет несколько неизвестных параметров . Для нахождения этих параметров составляют критерий качества аппроксимации.

В методе наименьших квадратов критерий качества примет вид

.

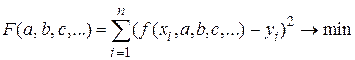Для нахождения неизвестных параметров a, b, c, …, обеспечивающих минимальное значение критерию качества, используют необходимый признак экстремума функции нескольких переменных. Согласно данному признаку в точках экстремума функции нескольких переменных все частные производные либо равны нулю, либо не существуют. Функция 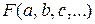данного вида является дифференцируемой, поэтому при оптимальных значениях параметров a, b, c, … все частные производные критерия качества должны равняться нулю, т. е.

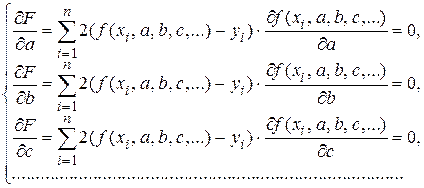
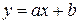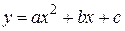В качестве аппроксимирующих функций часто используют функции следующего вида: 1) ; 2) ; 3) .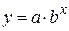

Составим системы уравнений для нахождения параметров аппроксимирующих функций.

1. В случае, когда 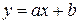критерий качества имеет вид

.

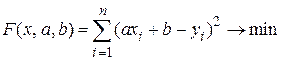Найдем частные производные этой функции, получим систему для нахождения a, b.

Û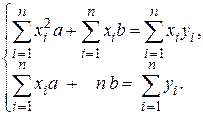

2. В случае, когда 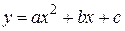критерий качества имеет вид

.

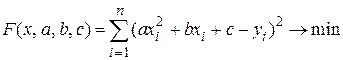Найдем частные производные этой функции, получим систему для нахождения коэффициентов a, b, с.

Û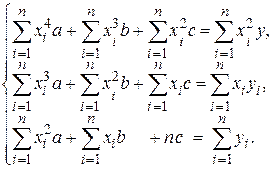

3. В случае, когда аппроксимирующая функция имеет вид 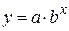, необходимо сначала прологарифмировать эту функцию 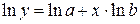. Тогда критерий качества

.

Система для нахождения ln a и ln b имеет вид

Û

После того, как будут найдены логарифмы ln a и ln b нужно найти a и b.

Пример 3.26. Заапроксимировать опытные данные

	-2	-1

многочленом второй степени 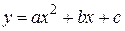. На рисунке изобразить опытные данные («жирными точками») и график аппроксимирующей функции. Вычислить значение критерия качества.

Вычисления коэффициентов системы для нахождения коэффициентов a, b, c приведены в таблице.

i
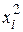
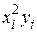
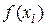
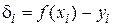
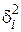
	-2			-8		-10		5,06	0,06	0,0036
	-1			-1		-3		2,57	-0,43	0,1849
								1,94	0,94	0,8836
								3,17	-0,83	0,6889
								6,86	0,86	0,7396
S										2,5006

Составляем систему для нахождения коэффициентов a, b, c и решаем ее.

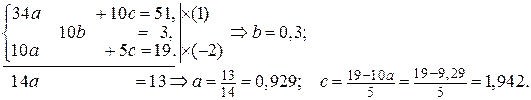
Аппроксимирующая функция .

Рис. 52

Опытные данные в виде точек и график аппроксимирующей функции приведены на рис. 52.

Дата добавления: 2014-01-11