Функции двух переменных

Достаточный признак условного экстремума

Пусть решается задача на условный экстремум

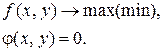
Запишем функцию Лагранжа

.

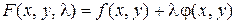Составим систему для нахождения критических точек

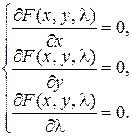
Пусть в результате решения этой системы найдена критическая точка 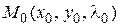. Тогда в этой точке равны нулю частные производные

,

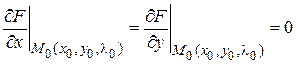следовательно, и дифференциал первого порядка .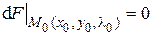

Наличие экстремума функции 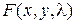в точке 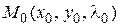определяется по тому, что является или нет знакоопределенной функцией приращение функции 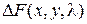в окрестности этой точки. Ввиду того, что дифференциал первого порядка в этой точке равен нулю, в первом приближении 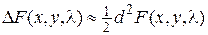. Если в критической точке 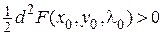, то 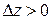и точка 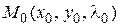является точкой минимума. Если же 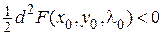, 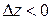и точка 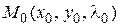является точкой максимума.

Дифференциал второго порядка функции трех переменных является квадратичной формой относительно .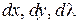

.

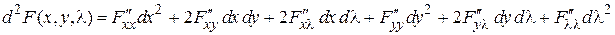В матричной записи этот дифференциал имеет вид

.

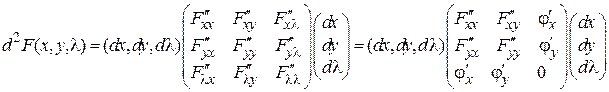Данную квадратичную форму можно исследовать на знакоопределееность с помощью критерия Сильвестра.

Согласно данному критерию, для того чтобы квадратичная форма была знакоположительной в некоторой d-окрестности точки 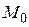, т.е.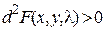 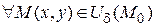, должны быть положительными все три главных минора матрицы этой формы.

, , .

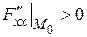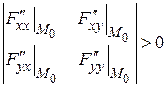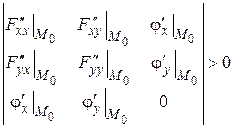В этом случае функция 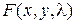будет иметь минимум в точке .

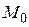Для того чтобы квадратичная форма была знакоотрицательной в некоторой d-окрестности точки 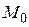, т.е.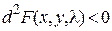 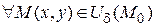, должны быть отрицательными первый и третий главные минора матрицы, а второй минор - положительный.

. , .

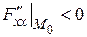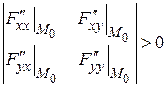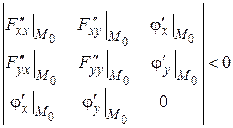В этом случае функция 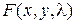будет иметь максимум в точке .

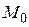В более удобном виде достаточный признак на условный экстремум функции двух переменных в критической точке 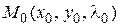записывают в виде одного определителя

.

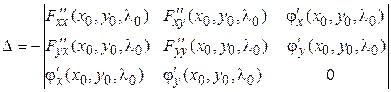Если D > 0, то 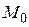- точка минимума, если D < 0, то 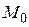- точка максимума.

Пример 3.27. Найти наибольший объем и длину ребер прямоугольного параллелепипеда, если его полная поверхность равна 2 а.

Обозначим длины ребер параллелепипеда через x, y, z. Тогда его объем 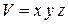, а полная поверхность равняется 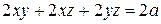. Поделим это равенство на 2, получим уравнение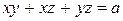, которое является ограничением при нахождении максимального объема параллелепипеда. Таким образом, задача формулируется следующим образом.

Найти максимум функции

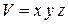
при условии, что ее переменные удовлетворяют уравнению

.

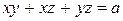Запишем функцию Лагранжа

.

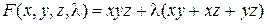Составим систему уравнений для нахождения критических точек.

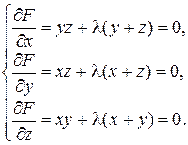
Умножим первое уравнение на х, второе на y, а третье на z и сложим, получим

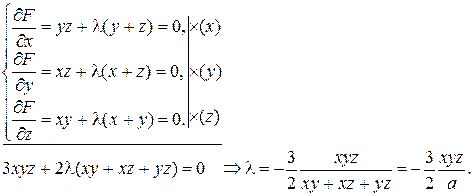
Подставим это значение l в систему уравнений и поделим первое уравнение на yz, второе на xz, а третье на xy.

.

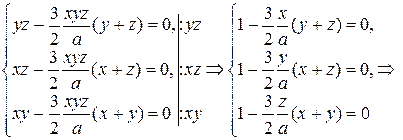
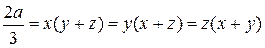Отсюда получаем

,

,

.

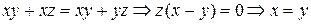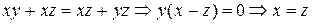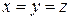Из равенства 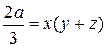получаем .

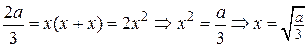Так как все ребра параллелепипеда равны 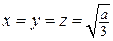, то объем .

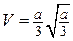Пример 3.28. Найти условные экстремумы функци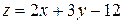и при 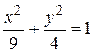(Рис. 54).

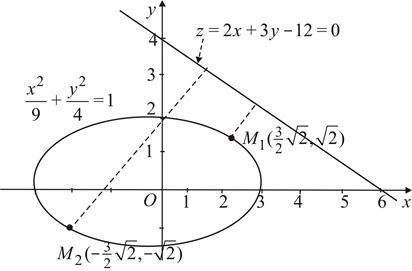
Рис. 54

Запишем функцию Лагранжа

.

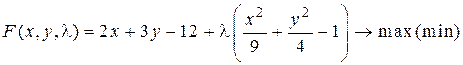Составим систему для нахождения критических точек

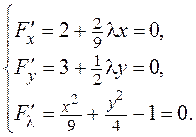
Из первого и второго уравнений найдем .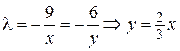

Из третьего уравнения получим .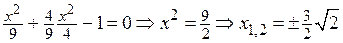

Тогда , .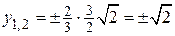

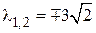Критические точки 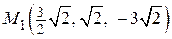, 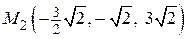исследуем на экстремум по достаточному признаку.

Найдем частные производные второго порядка: , , , , , .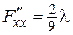

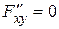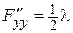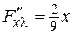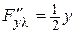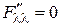Вычисляем значения этих производных в критической точке 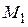и составляем определитель D.

, , ,

, , .

.

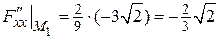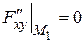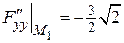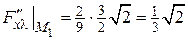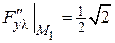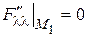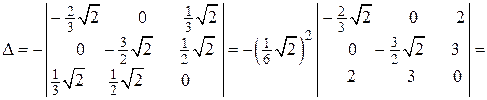
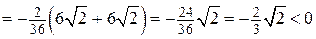Следовательно, в точке 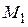функция имеет локальный максимум. Вычисляем значение функции в этой точке

.

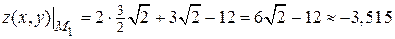Вычисляем значения производных функции 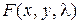в критической точке 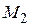и составляем определитель D.

, , ,

, , .

.

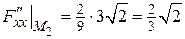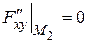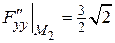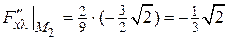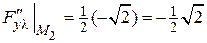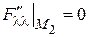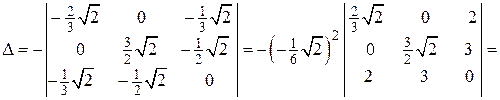
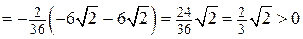Следовательно, в точке 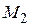функция имеет локальный минимум. .

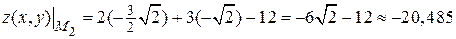О т в е т. 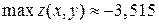в точке ;

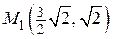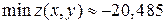в точке .

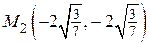Дата добавления: 2014-01-11