Использование буквенных индексов

Большинство задач механики жидкости будем рассматривать в декартовой системе координат. Но вместо обычного обозначения координат x, y, z введем обозначения x₁, x₂, x₃, т.е. индексную форму записи величин. Более кратко координаты можно записать, если использовать буквенный индекс, определив значения, которые он может принимать: x₁, x₂, x₃ Þ x_i, i= 1, 2, 3.

При такой записи предполагается, что скалярная величина изображается без индекса, векторная величина – с одним индексом, тензорная – с двумя индексами. Используя буквенные индексы, будем руководствоваться следующими правилами.

1.Правилом суммирования. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.

2.Индекс, встречающийся один раз (свободный индекс), должен пробегать значения от 1 до 3.

Таким образом, уравнение с одним свободным индексом означает запись трех уравнений. Очевидно, что для двумерного движения суммирование по немому индексу производят от 1 до 2, а свободный индекс принимает значения 1 и 2. В одномерном движении необходимости в подобных индексах нет.

Правило суммирования и определение свободного индекса можно относить не только к векторам, а вообще к любой записи и любым операциям. Так, например, запись

означает, что вектор b_i имеет три проекции:

Здесь индекс k – немой, индекс i – свободный. Немой индекс потому так называется, что при суммировании он заменяется цифрами, поэтому немой индекс пропадает и его можно заменить любой другой буквой. Можно, например, заменить индекс k на j, но не на i, так как i в данном случае принят в качестве свободного индекса (неповторяющегося).

В другом примере свободный индекс отсутствует: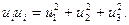

Нужно отметить, что все члены уравнения должны иметь один и тот же свободный индекс (либо вообще не иметь свободного индекса). Это означает, что все члены уравнения представляют проекцию на одну и ту же ось координат.

При записи векторных операций вводятся два символа.

1. Символ Кронекера. Он определен следующими свойствами:

δ _ij =1 при i=j, δ _ij =0 при .

2. Тензор перестановок по определению обладает следующими свойствами:

e_ijk= 1 при циклическом порядке индексов: 1, 2, 3, 1...

e_ijk=- 1 при антициклическом порядке индексов: 3, 2, 1,..

e_ijk= 0, если любые два индекса равны.

Пусть даны два вектора a и b, которые в индексной записи задаются компонентами a_i и b_i.

Скалярное произведение двух векторов является скаляром и является суммой произведений одноименных проекций: a · b=a ₁ b ₁ +a ₂ b ₂ +a ₃ b ₃.

Следовательно, в индексной записи скалярное произведение выглядит так: a · b =a_ib_i.

Векторное произведение является вектором, i – проекцию которого можно записать с помощью тензора перестановок: (a×b) _i = e_ijka_jb_k.

Компоненты этого вектора:

(a×b)₁= a ₂ b ₃ – a ₃ b ₂;

(a×b)₂= a ₃ b ₁ – a ₁ b ₃;

(a×b)₃= a ₁ b ₂ – a ₂ b ₁.

Вихрь (ротор) вектора является вектором, и его проекции определяются формулой: (rot a) _i 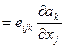, согласно которой

(rot a)₁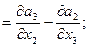

(rot a)₂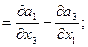

(rot a)₃

Градиент скалярной функции φ является вектором:

с проекциями:

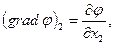
Дивергенция вектора a является скалярной величиной

div a = .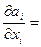

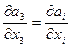Дата добавления: 2014-01-11