Субстанциональная производная или производная по направлению движения жидкой частицы

Пусть имеется величина g_j(x_i,t), характеризующая какое-то свойство жидкости, движущейся в контрольном объеме. Значение этой величины зависит от координатыточки х_i объема, в которой рассматривается величина g_j и от скорости перемещения из одной точки пространства в другую. Следовательно, величина g_j является сложной функцией координат и времени. Поэтому полная производная этой величины (полная скорость изменения во времени) будет равна . Здесь слагаемое - локальная составляющая скорости из-менения величины g_j, показывающая изменение ее за единицу времени в фиксированной точке x_i пространства; - конвективная, переносная составляющая скорости изменения рассматриваемой величины, показывающая изменение g_j в единицу времени, произошедшее из-за перехода из одной точки пространства в другую; - скорость перемещения жидкой частицы из одной точки пространства в другую; х_i - координата точки пространства. Если перемещение в пространстве осуществляется вдоль линии тока, то производная = u_i, т.е. равна скорости жидкости в точке x_i. Таким образом, - есть производная величины g_j по направлению движения жидкости в точке, субстанциональная производная величины g _j, эйлерова производная величины g_j. В дальнейшем мы, для краткости, будем называть ее полной производной величины g_j. Если рассматриваемой величиной является местная скорость жидкости u_j, то полное ускорение жидкости в любой точке контрольного объема будет определяться выражением .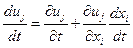

Теорема Остроградского – Гаусса, согласно которой можно преобразовать поверхностный интеграл в объемный, формулируем так: поток вектора b через замкнутую поверхность S, ограничивающую объем V, равен объемному интегралу от дивергенции этого вектора. Индексная запись этой теоремы имеет вид:

.

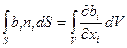Здесь n_i – вектор внешней нормали к элементу поверхности dS, скалярное произведение двух векторов b_in_i представляет собой нормальную к площадке dS составляющую вектора b - b_n = | b | |n|· cos (b ^ n). Если угол между векторами b и n острый, то скалярное произведение будет положительным, нормальная составляющая вектора b совпадает по направлению с направлением внешней нормали n. Если же угол между рассматриваемыми векторами тупой, то их скалярное произведение отрицательно и нормальная составляющая вектора b будет иметь направление, противоположное направлению внешней нормали n.

В заключение приведем описание основной леммы механики сплошной среды. Если интеграл от функции f(x_i), непрерывной в области V, взятый по произвольной области , равен нулю, то функция f(x_i)во всей области V.

Доказательство. Пусть функция f (x_i)в некоторой точке M . Тогда в силу непрерывности найдется такая окрестность точки M, в которой функция f (x_i) сохраняет свой знак и, следовательно, интеграл, взятый по этой окрестности, будет отличен от нуля. Это противоречит условию леммы.

Дата добавления: 2014-01-11