
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Тейлора. Пусть произвольная функция с хорошими свойствами рассматривается на какой-либо окрестности точки
|
|
|
|
Пусть произвольная функция с "хорошими" свойствами  рассматривается на какой-либо окрестности точки
рассматривается на какой-либо окрестности точки 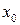 . Найти многочлен
. Найти многочлен 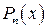 заданной степени
заданной степени 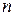 так, чтобы отклонение
так, чтобы отклонение 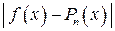 на
на  было наименьшим.
было наименьшим.
Ищем 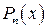 в виде многочлена по степеням разности
в виде многочлена по степеням разности 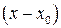 :
: 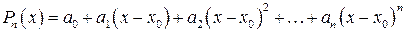 .
.
Тогда естественно потребовать выполнение соотношений
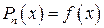 при
при  , т.е.
, т.е. 
 ;
;
 при
при  , т.е.
, т.е.
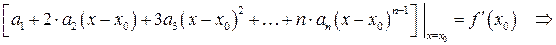

 ;
;
 при
при  , т.е.
, т.е.
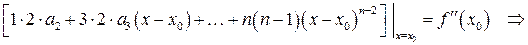

 .
.
Аналогично  и далее
и далее 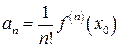 .
.
Определение(многочлена Тейлора).
Если для  ,
, 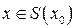 существуют производные
существуют производные 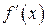 ,
,  ,
, 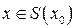 , то многочлен
, то многочлен
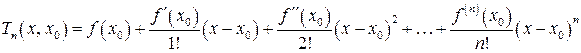
называется многочленом Тейлора n – го порядка функции  по степеням разности
по степеням разности 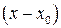 .
.
В этом случае говорят, что "функция  "порождает" свой
"порождает" свой
многочлен Тейлора в точке 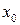 ".
".
Покажем, что именно многочлен Тейлора  функции
функции  задает наилучшее локальное приближение этой функции. Для этого оценим погрешность приближения
задает наилучшее локальное приближение этой функции. Для этого оценим погрешность приближения 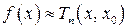 , т.е. оценим на
, т.е. оценим на  функцию
функцию 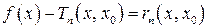 .
.
1.  – качественная характеристика погрешности (форма Пеано).
– качественная характеристика погрешности (форма Пеано).
В самом деле, рассмотрим
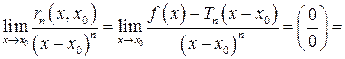
(применим последовательно "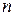 " раз правило Лопиталя)
" раз правило Лопиталя)
 ,
,
а это означает, что 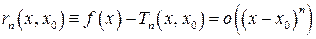 ,
,
т.е.  – формула Тейлора "
– формула Тейлора "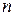 "-го порядка для функции
"-го порядка для функции  по степеням разности
по степеням разности 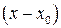 с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
2. 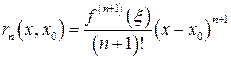 ,
,  – между
– между 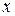 и
и 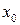 –количественная характеристика погрешности (форма Лагранжа).
–количественная характеристика погрешности (форма Лагранжа).
В самом деле, преобразуем отношение
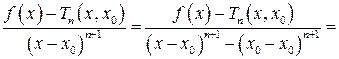
(по теореме Коши: 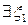 между
между 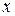 и
и 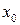 ;
;  – параметр)
– параметр)
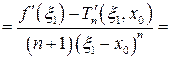

(по теореме Коши:  между
между  и
и 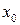 ;
; 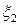 – параметр)
– параметр)
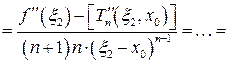
(после "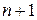 "-кратного применения теоремы Коши:
"-кратного применения теоремы Коши:  между
между  и
и 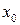 , т.е. между
, т.е. между 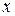 и
и 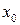 )
)
 .
.
Итак, если функция 
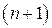 раз дифференцируема в окрестности точки
раз дифференцируема в окрестности точки  , причем
, причем 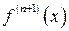 – непрерывная функция в этой окрестности, то
– непрерывная функция в этой окрестности, то
 ,
,
где  – некоторая точка между
– некоторая точка между 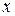 и
и 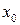 , т.е. функция представима
, т.е. функция представима
по формуле Тейлора "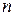 "-го порядка по степеням разности
"-го порядка по степеням разности 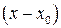 с остаточным членом в форме Лагранжа.
с остаточным членом в форме Лагранжа.
При 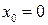 формулу Тейлора называют иногда формулой
формулу Тейлора называют иногда формулой
Маклорена и записывают
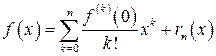 .
.
Пример 1. Разложить функцию  в окрестности точки
в окрестности точки 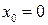 , взяв
, взяв 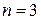 .
.
Решение. Воспользуемся формулой Маклорена при 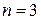 . Найдем производные
. Найдем производные 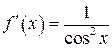 ;
;  ;
;
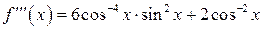 ; отсюда
; отсюда  ,
, 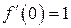 ,
,  ,
, 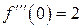 . Получаем
. Получаем 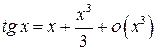 .
.
Пример 2. Убедиться самостоятельно в правильности разложений функции в окрестности 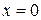 по степеням
по степеням 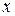 :
:
 , где
, где  лежит между
лежит между 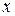 и 0;
и 0;
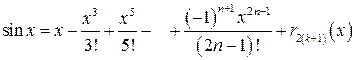 ,
,
 .
.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 393; Нарушение авторских прав?; Мы поможем в написании вашей работы!