Преобразование координат

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Геометрия – предмет, изучающий пространственные формы реального мира.

Аналитическая геометрия - предмет, изучающий геометрические образы при помощи алгебры.

В аналитической геометрии, с одной стороны, удается использовать аппарат алгебры в задачах геометрии, с другой стороны, решения многих задач алгебры получают наглядную геометрическую интерпретацию. Таким образом, достигается синтез двух важнейших отраслей математики, наблюдается их взаимопроникновение. В основе аналитической геометрии лежит метод координат, позволяющий определять точку пространства несколькими числами (координатами), а геометрические образы (линии, поверхности) – уравнениями, что дает возможность:

- описывать свойства фигур с помощью соотношений, связывающих координаты точек этих фигур;

- изучать (исследовать) эти соотношения средствами алгебры и анализа;

- делать выводы о геометрических свойствах фигур на основе исследования описывающих их соотношений.

Ниже потребуется переходить от одной плоской прямоугольной системы координат к другой плоской прямоугольной системе координат. Рассмотрим преобразование координат, происходящее при таком переходе. Пусть XOY исходная прямоугольная система координат и x, y – координаты произвольной точки M в этой системе. И пусть 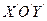- новая система координат, начало координат, которой O^’ смещено относительно соответствующих осей исходной системы в точку C c координатами (a,b) и координатные оси повернуты относительно соответствующих осей исходной системы на угол a. При этом координаты все той же точки M в новой системе обозначим через x^’ и y^’ (рис. 27).

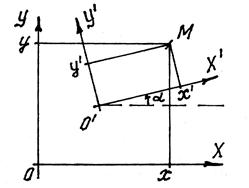Рис. 27

Координаты x и y исходной системы координат выражаются через координаты и 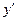новой системы по формулам

(2.21)

а координаты новой системы через координаты исходной системы

(2.22)

Уравнение смещенной параболы имеет вид

, (2.23)

что показывается с использованием преобразований координат (2.21)-(2.22). Парабола, соответствующая уравнению (2.23), приведена на рис. 28.

Рис. 28

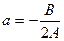Уравнению (2.23) соответствует парабола, ось симметрии которой параллельна оси ординат. Вершина этой параболы имеет координаты и 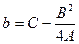. Ветви параболы обращены вверх или вниз в зависимости от того, положительно число A или отрицательно.

Равносторонняя гипербола, асимптотами которой являются оси координат, имеет уравнение

(2.24)

или 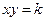, что так же показывается с использованием формул (2.21) -(2.22). Гиперболы, соответствующие уравнению (2.24), приводятся на рис. 29.

Рис. 29

Сплошной линией приведена гипербола (2.24), когда 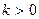, штриховой, когда .

Дата добавления: 2014-01-13