Прямая линия

Существуют различные виды уравнений прямой линии на плоскости, каждое из которых лучше используется при решении той или иной конкретной задачи в зависимости от задания тех или иных параметров прямой линии.

Уравнение прямой, проходящей через данную точку в данном направлении имеет вид

, (2.4)

где (2.4) уравнение рассматриваемой прямой 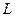(рис. 14), точка , 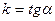- угловой коэффициент, 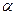- угол между прямо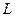й и

осью OX – угол на который нужно повернуть ось до совмещения с прямой против хода часовой стрелки.

Рис. 14

Уравнение прямой с угловым коэффициентом:

y=kx+b, (2.5)

где, как и ранее, 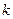- угловой коэффициент; 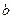- отрезок, отсекаемый прямой

Рис. 15

L (рис.15) на оси OY (положительное или отрицательное число).

Общее уравнение прямой имеет вид

. (2.6)

Здесь 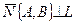. Доказывается, что в плоской декартовой прямоугольной системе координат всякая прямая определяется уравнением первой степени относительно текущих координат и каждое уравнение первой степени относительно текущих координат определяет прямую. Линии, определяемые уравнениями первой степени в декартовых координатах, будем называть линиями первого порядка. И, следовательно, каждая прямая – линия первого порядка; всякая линия первого порядка - прямая.

Уравнение прямой, проходящей через две заданных точки:

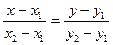, (2.7)

где M₁ (x₁,y₁) и M₂ (x₂,y₂) – точки принадлежащие рассматриваемой прямой L.

Уравнение прямой в отрезках:

,(2.8)

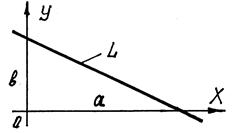где a и b – соответственно отрезки, отсекаемые прямой L на координат-

Рис. 16

ных осях OX и OY (рис. 16).

Нормальное уравнение прямой.

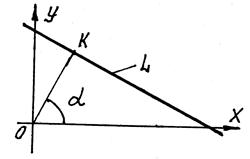
Пусть расстояние от начала координат до искомой прямой L - OK = p (рис. 17) и угол между перпендикуляром (нормалью) опущенным из начала координат на прямую L и осью OX равен a, тогда

(2.9)

Рис. 17

Уравнение (2.9) называется нормальным уравнением прямой, т.к. оно определяется нормалью OK, идущей из начала координат на линию L. Необ-

ходимо отметить следующие свойства нормального уравнения прямой:

1. Поскольку 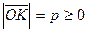, то (-p) 0;

2. 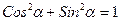, т.е. сумма квадратов коэффициентов нормального уравнения прямой равна единице.

Таким образом, если в уравнении первой степени относительно x и y наблюдается выполнение отмеченных свойств, то такое уравнение - нормальное уравнение прямой.

В некоторых случаях есть необходимость перейти от общего уравнения прямой L - Ax+By+C=0 к нормальному виду этого уравнения. Для этого необходимо помножить обе части этого уравнения на нормирующий множитель 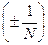, где и знак или "+", или “-“ выбирается противоположным знаку свободного члена C в общем уравнении прямой. В этом случае уравнение - нормальное уравнение прямой L, поскольку и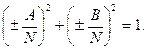

Дата добавления: 2014-01-13