
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства математического ожидания. Свойство. Математическое ожидание постоянной величины равно этой постоянной
|
|
|
|
Свойство  . Математическое ожидание постоянной величины равно этой постоянной
. Математическое ожидание постоянной величины равно этой постоянной
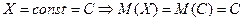 .
.
Доказательство. Действительно, пусть случайная величина 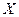 равна
равна 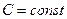 с вероятность
с вероятность  . Тогда по определению математического ожидания:
. Тогда по определению математического ожидания:
 .
.
Что и требовалось доказать.
Свойство  . Постоянный множитель можно вносить за знак математического ожидания
. Постоянный множитель можно вносить за знак математического ожидания
 , где
, где  .
.
Доказательство. Докажем для случайной величины 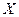 , которая принимает конечное число
, которая принимает конечное число  значений
значений  . По определению математического ожидания:
. По определению математического ожидания:

 .
.
Отсюда, вынося константу за знак суммы, получим:
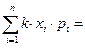

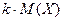 .
.
Что и требовалось доказать.
Свойство 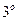 . Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий этих величин:
. Математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий этих величин:
 .
.
Доказательство. Докажем для математического ожидания величины, составленной из суммы двух случайных величин 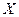 и
и  , причем случайная величина
, причем случайная величина 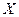 , принимает конечное число
, принимает конечное число  значений
значений  , а случайная величина
, а случайная величина  , принимает конечное число
, принимает конечное число 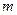 значений
значений  . Тогда математическое ожидание суммы двух величин
. Тогда математическое ожидание суммы двух величин 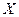 и
и  равно:
равно:

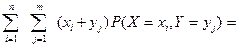
 .
.
Попробуем разобраться с первой двойной суммой
 .
.
В ней от значения 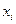 не зависит внутренняя сумма, поэтому вынесем
не зависит внутренняя сумма, поэтому вынесем 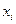 за знак этой суммы:
за знак этой суммы:
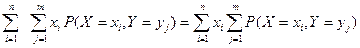 .
.
Событие, состоящее в том, что 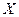 примет значение
примет значение 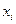 (вероятность этого события равна
(вероятность этого события равна 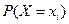 ), влечёт за собой событие, которое состоит в том, что
), влечёт за собой событие, которое состоит в том, что  примет значения
примет значения
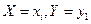 или
или 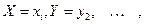 или
или  ,
,
а вероятности этих несовместных событий равны соответственно:
 или
или  или
или  .
.
Тогда вероятность 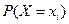 первоначального события
первоначального события 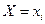 равна (по теореме о сложении вероятностей несовместных событий):
равна (по теореме о сложении вероятностей несовместных событий):

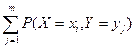 .
.
Поэтому первая двойная сумма равна:
 .
.
Последнее же равенство следует из определения математического ожидания.
Со второй двойной суммой поступим аналогично, но прежде заметим, что она не изменится, если поменять порядок суммирования:
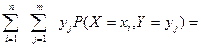
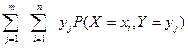
(Это известное свойство можно проверить, расписав его для случаев  или
или  ). А далее (вдоль по проторенной тропе):
). А далее (вдоль по проторенной тропе):
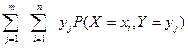

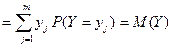 .
.
Поэтому окончательно получаем:

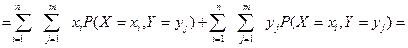
 .
.
Что и требовалось доказать.
Свойство 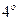 . Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
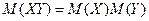 .
.
Без доказательства (для заинтересовавшихся студентов это доказательство – повод повысить итоговую оценку).
Пример. Вероятность попадания в мишень при одном выстреле равна 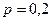 . Найти число независимых выстрелов, обеспечивающее математическое ожидание равное
. Найти число независимых выстрелов, обеспечивающее математическое ожидание равное  попаданиям в мишень (например, при стрельбе по кораблю).
попаданиям в мишень (например, при стрельбе по кораблю).
Решение. Пусть случайные величины 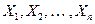 - есть число попаданий в мишень при каждом из
- есть число попаданий в мишень при каждом из  выстрелов. Тогда, согласно условию задачи, все эти случайные величины
выстрелов. Тогда, согласно условию задачи, все эти случайные величины  имеют один и тот же закон распределения
имеют один и тот же закон распределения

| 
| 
|
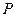
| 
| 
|
Математическое ожидание этих случайных величин равно
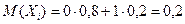 .
.
Математическое ожидание числа попаданий в мишень при  выстрелах равно
выстрелах равно  . По свойству
. По свойству 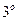 (математического ожидания)
(математического ожидания)

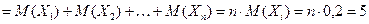 ,
,
где последнее равенство записано в силу условия задачи. Отсюда
 .
.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 437; Нарушение авторских прав?; Мы поможем в написании вашей работы!