Свойства дисперсии. Свойство. Дисперсия постоянной величины равна нулю

Свойство . Дисперсия постоянной величины равна нулю

.

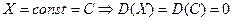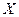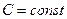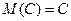­ Доказательство. Действительно, пусть случайная величина равна с вероятность . Поскольку тогда , то по определению дисперсии:

.

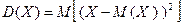
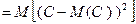
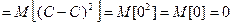Что и требовалось доказать.

Свойство . Постоянный множитель можно вносить за знак математического ожидания, но в квадрате

, где .

Доказательство. Используя определение дисперсии и свойство математического ожидания, получим:

.

Что и требовалось доказать.

Свойство 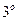. Дисперсия равна математическому ожиданию квадрата минус квадрат математического ожидания

.

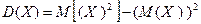
Доказательство. Используя определение дисперсии и свойство 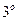математического ожидания, получим:

.

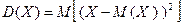
Поскольку математическое ожидание – суть константа, то по свойству , а затем по свойству математического ожидания, приходим к следующему:

.

Теперь, приводя подобные, получаем:

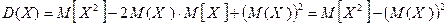
Что и требовалось доказать.

Свойство 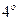. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

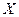, если и - независимы.

Без доказательства (для заинтересовавшихся студентов это доказательство – повод повысить итоговую оценку).

Свойство 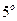. Дисперсия случайной величины ограничивает вероятность ее отклонение от своего математического ожидания (неравенство Чебышева П.Л.:

.

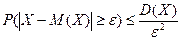Пример. При ракетной стрельбе в «заданный район» среднеквадратическое отклонение от цели имеет значение . Оценить радиус круга безопасности, где с вероятностью не мене 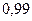ракеты не ложатся?

Решение. Пусть 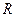- координата точки падения по дальности. Тогда вероятность выхода за -зону (по неизвестному пока Вам неравенству Чебышева) ограничена следующим: , но она должна быть не больше 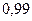. Это будет выполнено, если , т. е. при .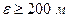

Заметим: если предположить, что дальность распределена по нормальному закону, то: 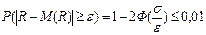, а значит 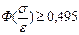, или при . Как видим знание закона распределения существенно уточняет круг безопасности!

__________________

Таким образом, мы ввели и узнали свойства основных числовых характеристик случайной величины.

Рис. 8.1. Геометрическая иллюстрация понятий математического ожидания ,

моды и дисперсии случайной величины.

На рис. 8.1 показано, что математическое ожидание 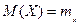характеризует центр распределения. Среднее ожидаемое значение величины, которое в общем случае асимметрии не совпадает с наиболее вероятным значением величины, характеризуется ее модой 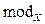. Геометрически оно изображается как координата центра тяжести фигуры, образованной осью 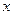и линией функции . Дисперсия 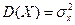и характеризуют средний ожидаемый разброс (широту) значений величины возле математического ожидания.

Дата добавления: 2014-01-14