Основные показатели динамики товарооборота в 1987-1991 гг

Показатель
Товарооборот, тыс. руб., у	885,7	932,6	980,1	1028,7	1088,4
Абсолютный прирост, тыс. руб.
базисный	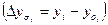-	932,6-885,7=46,9	980,1-885,7=94,4	143,0	202,7
цепной	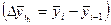-	932,6-885,7=46,9	980,1-932,6=47,5	48,6	59,7
Темп роста, %
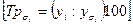
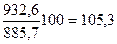
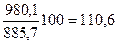
базисный	-			116,1	122,9
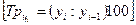
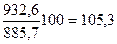
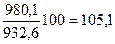
цепной	-			104,9	105,8
Темп прироста, %
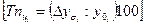
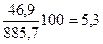
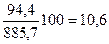
базисный	-			16,1	22,9
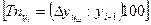
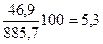
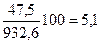
цепной	-			4,9	5,8
Темп наращивания, %
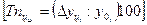
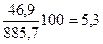
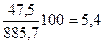
	-			5,5	6,8

Показатели базисных темпов роста табл. 9.3 свидетельствуют, что по сравнению с 1987 г. происходило систематическое увеличение товарооборота магазина, достигшего в 1991 г. 122,9% базисного уровня. Цепные темпы роста показывают, что в развитии товарооборота имело место замедление погодовых темпов (%): 105,3> 105,1 >104,9< 105,8.

Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:

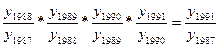( 9.6)

Так, подставляя в левую часть формулы (9.6) вычисленные в табл. 9.3 цепные темпы роста (в коэффициентах): 1,053 * 1,051 * 1,049 * 1,058, получаем базисный темп роста в 1991 г. =1,229.

Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Базисный темп прироста Тп_б вычисляется делением сравниваемого базисного абсолютного прироста 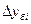на уровень, принятый за постоянную базу сравнения :

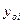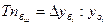(9.7)

Цепной темп прироста Тп_ц - это отношение сравниваемого цепного абсолютного прироста 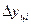_| к предыдущему уровню :

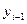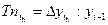(9.8)

Расчет темпов прироста по формулам (9.7) и (9.8) приведен в табл. 9.3. Между показателями темпа прироста и темпа роста имеется взаимосвязь:

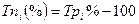(9.9)

(при выражении темпа роста в процентах).

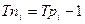(9.10)

(при выражении темпа роста в коэффициентах).

Формулы (9.9) и (9.10) используются для определения темпов прироста по темпам роста. Например, на основе вычисленного для 1991 г. базисного темпа роста товарооборота 122,9% по формуле (9.9) можно определить темп прироста:

Тп_б1991= 122,9 - 100 = 22,9%.

Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики. Например, если в I квартале 1990 г. объем реализации товаров А составил 92% уровня продажи этого товара в IV квартале 1989 г., то, применяя формулу (9.5), получим такой темп прироста:

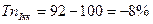
т. е. произошло сокращение продажи на 8%.

Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсифика­ции экономики измеряет наращивание во времени экономического потенциала.

Вычисляются темпы наращивания Тн делением цепных абсолютных приростов 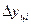на уровень, принятый за постоянную базу сравнения,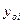

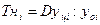(9.11)

Применение формулы (9.11) проиллюстрировано в табл. 9.3.

В отличие от вычисленных в табл. 9.3 цепных темпов прироста 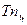, показывающих затухание, развитие товарооборота в 1988-1990 гг.: 5,3>5,1>4,9, темп наращивания Тн свидетельствует о наращивании из года в год объема товарооборота: 5,3<5,4<5,5<6,8.

Противоречивость вычисленных в табл. 9.3 показателей темпов прироста и наращивания объясняется особенностями принятого метода счета. Так, например, в ряду чисел 1,2,3,4,... при одинаковых цепных абсолютных приростах (равных 1) отношения чисел дают следующие результаты (%): 2/ 1*100=200, 3/2*100=150, 4/3*100=133 и т. д., т. е. налицо затухание темпа роста. Аналогичные действия производятся и при вычислении в табл. 9.5 темпов роста и прироста.

Из преобразований в формуле (9.11) следует, что темпы наращивания можно непосредственно определять по базисным темпам роста (пункты роста):

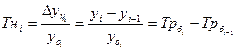(9.12)

Формула (9.12) удобна для практики, так как статистическая информация о динамике социально-экономических явлений публикуется чаще всего в виде

базисных рядов динамики.

Применение формулы (9.12) проиллюстрируем на базисных темпах роста товарооборота магазина (см. табл. 9.3). Для определения темпа наращивания объема товарооборота в 1991 г. найдем разность между базисными темпами роста 1991 и 1990 гг.:

Т_Н1991= 122,9 - 116,1 = 6,8%.

Дата добавления: 2014-01-11