Среднедневная реализация, тыс. руб

Квартал	1-й год	2-й год	3-й год	4-й год
I 75	247 420
II 263	298 441
III 326	366 453
IV 297	341 399

Особенностью данных табл. 9.5 являются периодическая колеблемость квартальных уровней, увеличение уровня продажи во II и III кварталах и некоторое снижение в IV квартале. Основная тенденция развития непосредственно не просматривается.

Для выявления основной тенденции развития методом скользящей средней прежде всего устанавливаются ее звенья. Звенья скользящей средней должны составляться из числа уровней, отвечающих длительности внутригодовых циклов в изучаемом явлении.

Для ряда динамики, отображающего развитие товарооборота по кварталам, скользящие средние обычно составляются из четырехчленных звеньев. Их расчет состоит в определении средних величин из четырех уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:

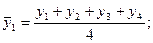
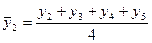и т.д.

В нашем примере исчисляются 13 скользящих средних (табл 9.6, гр. 3).

Таблица 9.6

Год, квартал	Исходные уровни	Скользящие средние у0	Сглаженные уровни с центрированием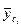

1-й год

I кв. 175

II" 263 1061:4=265, 25

III" 326 1133:4=283, 25 274, 25

IV" 297 1168:4=292, 0 287, 6

2-й год

I кв. 247 1208:4=302, 0 297, 0

II" 298 1252:4=313, 0 307, 5

III" 366 1425:4=356, 25 334, 6

IV" 341 1568:4=392, 0 374, 1

3-й год

I кв. 420 402, 9

II" 441 1655:4=413, 75 421, 0

III" 453 1713:4=428, 25 429, 0

IV" 393 1719:4=429, 25 430, 75

4-й год

I кв. 426 1727:4=431, 75 435, 37

II’’ 449 1756:4=439, 0 446, 62

III’’ 482 1817:4=454, 25

IV" 460

Для четного числа уровней каждое значение скользящей средней приходится на промежуток между двумя смежными кварталами. Так, первая скользящая средняя (265,25) записывается между II и III кварталами, вторая (283,25) -между III и IV кварталами и т. д. Для определения сглаженных уровней производится центрирование (с). Для III квартала определяется серединное значение между первой и второй скользящими средними: (265,25+283,25): 2=274,25 тыс. руб., для IV квартала центрируются вторая и третья скользящие средние: (283,25+292):2=287,6тыс. руб. и т. д.

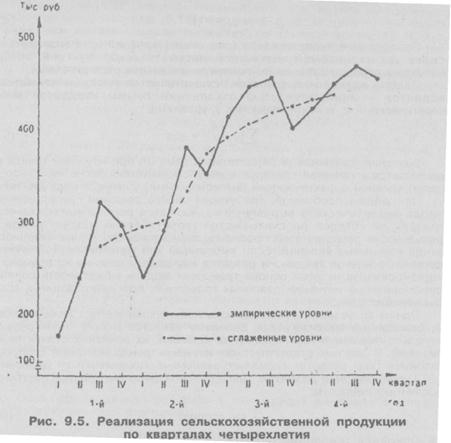
Полученные значения сглаженных уровней помещены в гр. 4 табл. 9.7. Из их графического изображения отчетливо видна основная тенденция развития комиссионной торговли (рис. 9.5).

При применении метода скользящей средней к ряду динамики месячных уровней рассчитываются 12-членные скользящие средние:

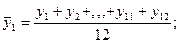
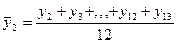
и т. д. с последующим центрированием полученных значений.

Если при сглаживании рядов динамики звенья скользящей средней составляются из нечетного числа уровней, то необходимость в центрировании отпадает.

Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получать обобщенную статистическую оценку тренда посредством этих методов невозможно. Решение этой более высокого порядка задачи - измерения тренда - достигается методом аналитического выравнивания.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития 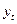рассчитывается как функция времени

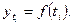(9.23)

Определение теоретических (расчетных) уровней 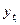производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики.

Подбор адекватной функции осуществляется методом наименьших квадратов - минимальностью отклонений суммы квадратов между теоретическими 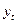и эмпирическими уровнями:

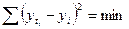(9.24)

Значение уравнения (9.24) состоит в том, что при изучении тренда оно принимается в качестве критерия оценки соответствия расчетных (теорети­ческих) уровней с фактическими (эмпирическими) уровнями ряда динамики.

Важнейшей проблемой, требующей своего решения при применении метода аналитического выравнивания, является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений. Если выбранный тип математической функции адекватен основной тенденции развития изучаемого явления во времени, то синтезированная на этой основе трендовая модель может иметь полезное применение при изучении сезонных колебаний, прогнозировании и других практических целях.

Одним из условий обоснованного применения метода аналитического выравнивания в анализе рядов динамики является знание типов развития социально-экономических явлений во времени, их основных отличительных признаков. В практике статистического изучения тренда различают следующие эталонные типы развития социально-экономических явлений во времени:

1) равномерное развитие. Для этого типа динамики присущи постоянные абсолютные приросты:

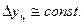(9.25)

Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображается уравнением прямолинейной функции:

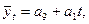(9.26)

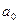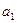где и - параметры уравнения; t - обозначение времени.

Параметр а, является коэффициентом регрессии, определяющим направление развития. Если 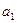>0, то уровни ряда динамики равномерно возрастают, а при 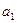<0 происходит их равномерное снижение;

2) равноускоренное (равнозамедленное) развитие. Этому типу дина­мики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов динамики изменяются с постоянными темпами прироста:

Т_пц 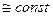(9.27)

Основная тенденция развития в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка:

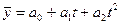(9.28)

В формуле (9.28) значения параметров а_о и а, идентичны параметрам, используемым в формуле (9.26). Параметр 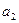характеризует постоянное изменение интенсивности развития (в единицу времени). При а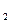>0 происходит ускорение развития, а при а₂<0 идет процесс замедления роста. Параметр а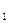может быть как со знаком плюс, так и со знаком минус;

3) развитие с переменным ускорением (замедлением). Для этого типа динамики основная тенденция развития выражается функцией параболы третьего порядка:

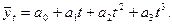(9.29)

В уравнении (9.29) параметр а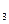отображает изменение ускорения. При а₃>0 ускорение возрастает, а при а₃<0 ускорение замедляется;

4) развитие по экспоненте. Этот тип динамики характеризуют стабильные темпы роста:

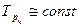(9.30)

Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией:

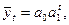(9.31)

где а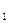- темп роста (снижения) изучаемого явления в единицу времени, т. е. интенсивность развития;

5) развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики:

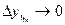(9.32)

Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией:

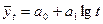(9,33)

При аналитическом выравнивании в рядах динамики можно применить и другие математические функции. Так, при изучении основной тенденции неудовлетворенного и реализованного спроса населения применяются:

степенная функция - 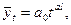(9.34)

функция гиперболы - 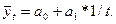(9.35)

Применение метода аналитического выравнивания при статистическом изучении тренда проиллюстрируем на примере.

Пример. По данным о розничном товарообороте региона в 1980-1985 гг. (табл. 9.7) нужно произвести анализ основной тенденции развития товарооборота.

Таблица 9.7

Год	Объем розничного това­рооборота, млрд. руб.	Темп роста по годам, %	Абсолютный прирост по годам, млрд. руб.
1980 11,18 1981 12,23 109,4 1,05 1982 13,28 108,6 1,05 1983 14,31 107,7 1,03 1984 15,36 107,3 1,05 1985 16,40 106,8 1,04

В среднем 14,32 107,9 1,04

Из табл. 9.7 видно, что развитие товарооборота происходило с затухающими темпами роста (гр. 3) и относительно стабильными абсолютными приростами (гр. 4).

Для установления в данном ряду динамики типа развития определяющим признаком является характер изменения абсолютных приростов. Поскольку при среднем абсолютном приросте, равном 1,04 млрд. руб., величина их изменений незначительная (+0,01 млрд. руб.), то анализируемый ряд динамики можно считать с равномерным развитием (см. (9.25)). Поэтому для аналитического выравнивания применяется функция (9.26) .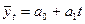

Для вычисления параметров функции (9.26) на основе требований метода наименьших квадратов (см. (9.24)) составляется система нормальных уравнений:

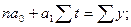
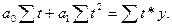(9.36)

Для решения системы уравнений (9.36) обычно применяется способ определителей, позволяющий получать более точные результаты за счет сведения к минимуму ошибки из-за округлений в расчетах параметров:

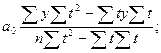(9.37)

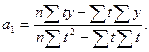(9.38)

Применительно к анализируемым данным для определения алгоритмов (9.37) и (9.38) составляется матрица расчетных показателей (табл. 9.8).

Таблица 9,8

Год	Объем розничного товарооборота, млрд руб.
1980 11,18 1 1 11,18 11,183
1981 12.23 2 4 24,46 12,226
1982 13,28 3 9 39,84 13,269
1983 14,31 4 16 57,24 14,312
1984 15,36 5 25 76,80 15,355
1985 16,40 6 36 98,40 16,398

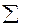62,76 21 91 307,92 82,743

По итоговым данным табл. 9.8 определяем по формуле (9.37):

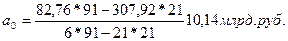
по формуле (9.38):

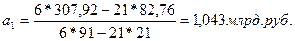(9.39)

По вычисленным параметрам производим синтезирование трендовой модели функции (см. формулу (9.26)):

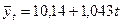
На основе модели (9.39) определяются теоретические уровни тренда (у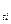) для каждого года анализируемого ряда динамики:

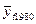
= 10,14 +1,043 *1 = 11,183 млрд. руб.

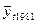=10,14 + 1,043*2 = 12226 млрд. руб.

………………………………………………..

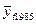= 10,14 +1,043 * 6 = 16,398 млрд. руб.

Вычисленные теоретические уровни помещены в гр. 6 табл. 9. 8. Правильность расчетов проверяется по равенству:

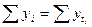(9.40)

Несовпадение в равенстве (9.40) на 0,017 млрд. руб. объясняется округлениями в расчетах.

Параметр а, трендовой модели (9.39) показывает, что объем розничного товарооборота региона возрастал в среднем на 1,043 млрд. руб. в год.

Практика статистического изучения тренда социально-экономических явлений показывает, что порой невозможно однозначно решить вопрос, какому типу развития больше всего отвечают показатели ряда динамики. Рассмот­ренные выше признаки классификации типов развития (абсолютные приросты, темпы роста и прироста) весьма схематичны. На практике ряды динамики с показателями, соответствующими признакам эталонных математических функций, скорее исключение, чем правило. Реальные условия формирования уровней развития социально-экономических явлений таковы, что совокупное действие факторов (постоянных, периодических, разовых) обусловливают такие изменения показателей ряда динамики, которые не согласуются с основными признаками типовых эталонных функций. Это осложняет выбор адекватной математической функции для аналитического выравнивания.

Но, как отмечалось выше, при изучении социально-экономических явлений приходится иметь дело со сложным механизмом взаимодействия факторов, формирующих тренд. Поэтому на основе качественного анализа не всегда возможно получать надежные выводы о типе развития в виде адекватной математической функции. В лучшем случае на основе качественного анализа может быть выдвинута рабочая гипотеза о возможных типах развития. Но выбор на этой основе конкретной математической функции весьма затруднителен. Особенно это относится к криволинейным функциям, теория которых разработана недостаточно.

Для подтверждения гипотезы о возможном типе развития можно использовать графический метод. Наглядное изображение анализируемого ряда динамики позволяет получать образное представление о размещении на поле графика эмпирических уровней. Это способствует лучшему осмыслению специфики изменений в ряду динамики. Но дать обобщенную статистическую оценку выявленного тренда графический метод не может.

Практика статистического изучения тренда с использованием средств современной вычислительной техники показывает, что в решении проблемы выбора адекватной математической функции определяющее значение имеет обеспеченность ЭВМ пакетом стандартных программ для машинной обработки исходной информации. Возможности широкого использования в анализе тренда современных ЭВМ позволяют выбрать наиболее адекватную трендовую модель. Быстродействие современных ЭВМ с большой емкостью памяти позволяет получать все необходимые для анализа тренда показатели, в том числе и применяемые для выбора адекватной математической функции.

Одним из применяемых в практике статистического изучения тренда показателей адекватности математической функции является стандартизованная ошибка аппроксимации :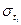

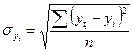(9.41)

Применение в изучении тренда формулы (9.41) основано на том, что за наиболее адекватную принимается функция, у которой стандартизованная ошибка аппроксимации минимальная.

Использование формулы (9.41) для подбора наиболее адекватной математической функции при статистическом изучении тренда проиллюстри­руем на примере.

Пример. По данным о розничном товарообороте региона (табл. 9.9) нужно произвести синтезирование трендовой модели товарооборота.

Разнохарактерность изменений погодовых темпов роста (103,5<105,3>102,8<104,4) и значительная колеблемость цепных абсолютных приростов (от 0,5 до 0,9 млрд. руб.) затрудняют определение типа динамики объема розничного товарооборота.

Таблица 9.9

Год	Объем розничного товарооборота, млрд руб.	Темп роста по годам, %	Абсолютный прирост по годам, млрд руб.
			.4
1985 16,4 - -
1986 16,9 103,5 0,5
1987 17,8 105,3 0,9
1988 18,3 102,8 0,5
1989 19,1 104,4 0,8

В среднем 17,7 103,9 0,67

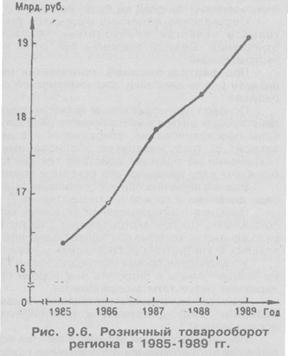
Для решения поставленной за­дачи, прежде всего в порядке пер­вого приближения, намечаются типы функций, которые могут отобразить имеющиеся в ряду динамики изме­нения. В помощь этому исходные данные табл. 9.9 изображаются гра­фически (рис. 9.6).

Из характера размещения уров­ней анализируемого ряда динамики на поле графика (рис. 9.6) можно сделать предположение о возмож­ном применении тренда при анали­тическом изучении ряда математи­ческих функций. Это может быть и уравнение прямолинейной функции (9.26), и уравнение показательной кривой (9.31), и уравнение параболы второго порядка (9.28), и уравнение параболы третьего порядка (9.29). Для выбора наиболее адекватной из них следует осуществить сравнительный анализ тренда исходных данных спосо­бом перебора решений по намеченным математическим функциям.

Для определения пара­метров математических функций при анализе тренда в ря­дах динамики используется способ отсчета времени от условного начала. Он осно­ван на обозначении в ряду ди­намики показаний времени та­ким образом, чтобы 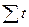=0. При этом в ряду динамики с нечет­ным числом уровней порядко­вый номер уровня, находяще­гося в середине ряда, обозна­чают через нулевое значение и принимают его за условное на­чало отсчета времени с интер­валом + 1 всех последующих уровней и -1 всех предыдущих уровней. Например, при n=5 обозначения времени будут -2, -1,0, +1, +2. При четном числе уровней, например п=6, поряд­ковые номера верхней полови­ны ряда (от середины) обозна­чаются числами: -1, -3, -5, а нижней половины ряда обозна­чаются: + 1, +3, +5.

При использовании спо­соба условного обозначения времени, когда 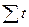=0, параметры математических функций определяются по формулам:

а) для прямолинейной функци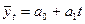и (при ):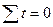

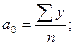(9.42)

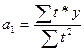(9.43)

б) для показательной функции :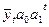

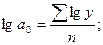(9.44)

Дата добавления: 2014-01-11