Штейнер теоремасы

Дененің кез келген өске қатысты инерция моменті өске параллель болатын, масса центрі арқылы өтетін өске қатысты инерция моменті мен дененің массасының өстерінің арақашықтығының квадратына көбейтіндісінің қосындысына тең болады.

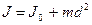(1.5.3.1)

мұнда 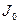- дененің масса центрі арқылы өтетін өске қатысты инерция моменті, 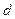- остердің арақашықтығы.

Мысал ретінде айналыс өсі бір ұшы арқылы ететін өзектің инерция моментін есептейік. Штейнер теоремасын қолданып төмендегідей өрнек жазуға болады.

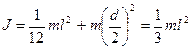
мүндағы 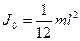- айналыс өсі масса центрі аркылы өтетін өзектің инерция моменті.

1.5.4 Қатты дененің қозғалыс мөлшері моментінің сақталу заңы

Қатты дене козғалмайтын өстен айналсын. Денені бірдей элементар бөлшектерге бөлейік (І.5.4.1-сурет).

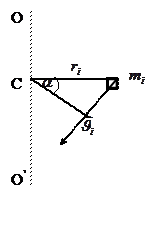
І.5.4.1-сурет

ОО' - айналыс өсі; m,- бөлшек массасы; 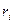- бөлшектің айналыс өсінен қашықтығы; 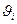- бөлшектің сызықтық жылдамдығы.

Қозғалыс мөлшері векторының моменті деп айналыс өсінде жататын және шамасы радиус-вектор мен қозғалыс мөлшері векторының геометриялық көбейтіндісіне тең болатын шаманы айтады.

Әр бөлшектің қозғалыс мөлшерінің моменті

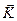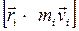= (1.5.4.1)

формуласымен анықталады.

Ендеше өске катысты катты дененің козғалыс мелшерінің моменті барлық бөлшектердің козғалыс мөлшері моменттерінің косындысына тең болады.

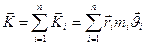
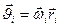
екендігін ескеріп козғалыс мөлшері моментінің модулі үшін мынадай теңдік жазуға болады:

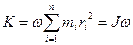(1.5.4.2)

мүндағы 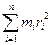= I дененің инерция моменті; 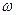- бұрыштық жылдамдығы.

(1.5.4.2)формуланыескеріп айналмалы қозғалыстың негізгі тендеуін мына түрде жазуға болады:

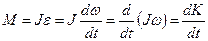(1.5.4.3)

Айналыс өсіне қатысты қозғалыс мөлшері моментінің уақыт бойынша туындысы сол өске қатысты күш моментіне тең болады.

(1.5.4.3) формуласынан

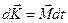(1.5.4.4)

деп жазуға болады.

Айналыс өсіне қатысты қозғалыс мөлшері моментінің өзгерісі сыртқы күш моменті импульсіне тең болады.

Сыртқы күштер моменті 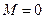болса, 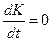, ендеше

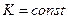(1.5.4.5)

(1.5.4.5) формуласы козғалыс мөлшері моментінің сакталу заңы делінеді. Бұл заңды қолданып төмендегідей өрнек жаза аламыз:

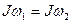(1.5.4.6)

Айналып тұрған дененің инерция моменті өзгерсе, онда бұрыштық жылдамдығы да өзгереді, бірақ олардың көбейтіндісі тұрақты болады.

Қозғалыс мөлшері моментінің сакталу заңын Жуковский скамьясы (орындығы) арқылы тәжірибе жасап көруге болады. Үйкеліс аз болатын өстен дөңгелек диск айналысқа келтіріледі (1.5.4.2-сурет).

Диск үстінде қолында жүгі (гирлер) бар адам екі қолын екі жағына иығының деңгейінде ұстап тұр дейік (1.5.4.2а- сурет).

Айналып тұрған адамның қозғалыс мөлшерінің моменті бар. Егер адам колын төмен түсірсе инерция моменті азаяды (І.5.4.2б-сурет). Қозғалыс мөлшері моментінің сақталу заңы бойынша бұрыштык жылдамдығы артады. Сондықтан 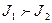болған жағдайда 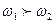болады.

Цирктегі акробаттар тізесін бүгу, денесін еңкейту аркылы инерция моментін азайтады, сол кезде бұрыштық жылдамдығы артады.

а) б)

1.5.4.2-сурет

1.5.5 Айналмалы қозғалыстағы дененің кинетикалық энергиясы

Дене қозғалмайтын өстен айналсын. Дененің әр бөлшегінің кинетикалық энергиясы:

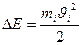
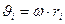формуласын ескеріп әр бөлшектің кинетикалық энергиясын

Д E_k 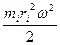(1.5.5.1)

деп жазуға болады.

Тұтас дененің кинетикалык энергиясын анықтау үшін барлық бөлшектердің кинетикалық энергияларын қосамыз.

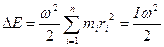(1.5.5.2)

мүндағы 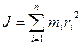- дененің инерция моменті.

Денені ц бұрышқа бұратын күш моментінің істейтін жұмысын анықтайық.

Денеге ОО' осіне қатысты күш моменті

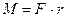(1.5.5.3)

болатын күш әсер етсін (І.5.5.1-сурет). Дене 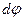бұрышка бұрылғанда А нүктесі 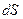доға ұзындығына жылжиды. Сол кездегі 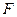күштің істейтін жүмысы

.

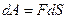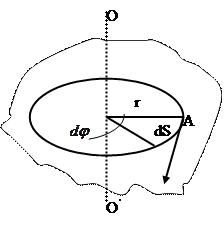
І.5.5.1-сурет

Сурет бойынша 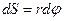, ендеше

(1.5.5.3) формуласы бойынша

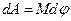
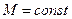болған жағдайда

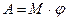(1.5.5.4)

Дене айналған кезде істелінген жұмыс күш моменті мен бұрылу бұрышының көбейтіндісіне тең болады.

Ал 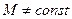болған жағдайды қарастырайық. Ол үшін айналмалы козғалыстың негізгі теңдеуінің екі жағын 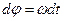-ға көбейтіп жіберейік. Сонда

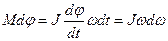
бұл өрнектен интеграл алғанда

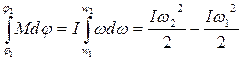(1.5.5.5)

шығады.

Айналмалы қозғалыс кезінде кинетикалық энергияның өзгерісі күш моментінің жүмысына тең болады.

Егер дене бір мезгілде ілгерілемелі және айналмалы қозғалыс жасаса оның толық кинетикалық энергиясы:

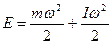(1.5.5.6)

формуласымен анықталады.

Дата добавления: 2014-10-15