Есеп мысалдары. 1. 1 см3 көлемде 0,1 МПа қысымда азоттың 2,7*1019 молекуласы әртүрлі бағытта әртүрлі жылдамдықпен

1. 1 см³ көлемде 0,1 МПа қысымда азоттың 2,7*10¹⁹ молекуласы әртүрлі бағытта әртүрлі жылдамдықпен қозғалады. Жылдамдықтарының вертикаль құраушылары 999-1001 м/с аралықта жататын молекулалардың саны 1,3*10¹². 1 л азотта осындай қанша молекула бар?

2.Жылдамдықтарының х өсі бойынша құраушыларының жылдамдықтары 3000-3010 м/с аралығында болатын сутегі молекулаларының санының осы бағыттағы жылдамдықтарының құраушылары 1500-1505 м/с аралықта жататын молекулалардың санына қатынасын табу керек.

3.Цилиндрдің бетіне қадамы h болатын винттік канал тілінген. Цилиндрдің бір жағында сиретілген газ, екінші хағында вакуум болсын. Молекулалар каналмен жылдам жұтылады және цилиндр 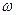бұрыштық жылдамдықпен айналады деп есептеу керек. Канал арқылы өтетін молекулалардың жылдамдығы қандай?

4. Жер бетінде азот молекулаларына қарағанда гелий молекулалары 10⁵ есе, ал сутегінікі 10⁶ есе аз. Қандай биіктікте гелий молекулаларының саны азот молекулаларының саныне тең болады? Сутегінікі ше? Атмосфераның оратша температурасы 27⁰С.

5.Бағытталған шоқ молекулаларының таралуы төмендегідей функциямен берілсін: 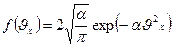. Молекула массасы m. Шоқ ені L аралықтан өткенде әр бір молекулаға F кедергі күш әсер ететін болса, таралу функциясы мен бірлік көлемдегі молекула саны қалай өзгереді?

6. Қандай да бір газдың молекулаларының ең ықтимал жылдамдығы 1820 м/с. Бұл қандай газ? Егер газ температурасы 127⁰С болса молекулалардың орташа арифметикалық және орташа квадраттық жылдамдықтары қандай?

2.6 Газ молекулаларының орташа соқтығысу саны.

Орташа еркін қозғалыс жолы

Молекулалардың бір бірімен соқтыққанға дейінгі жүретін еркін қозғалыс жолының ұзындығын анықтайық. Молекулалар саны өте көп және қозғалысы ретсіз болғандықтан орташа еркін қозғалыс жолының ұзындығын есептейік. Зерттеуді оңайлату үшін қарастырып отырған молекуладан басқа молекулалар қозғалмайды және осы молекуланың қозғалыс бағыты басқа молекулалармен соқтығысқаннан соң да өзгермейді деп есептейік. Молекуланы радиусы 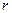, жылдамдығы 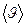шар деп алайық. Сонда молекула қашықтығы 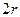- ден кіші болатын барлық молекулалармен соқтығысады.

Яғни жасаушының ұзындығы 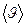, радиусы 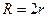болатын цилиндр ішіндегі барлық молекулалармен соқтығысады (2.6.1-сурет).

Цилиндр ішіндегі молекулалар саны 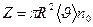болсын.. Басқа молекулалардың қозғалысын ескерсек, онда бірлік уақыттағы соқтығысу саны 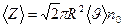болады, оны төмендегідей жазуға болады:

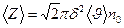(2.6.1)

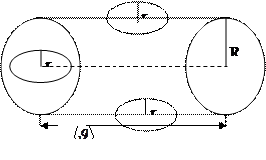
2.6.1-сурет

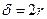- молекуланың эффектілік диаметрі..

Молекулалардың бір-бірімен соқтыққанға дейін жүрген жолын орташа еркін қозғалыс жолының ұзындығы дейді. Ол мына формуламен анықталады:

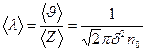(2.6.2)

2.7 Тасымалдау құбылысы

Термодинамикалық тепе-тең емес жүйелерде нәтижесінде энергияның, массаның, импульстің тасымалданулары жүзеге асатын қайтымсыз процесстер өтеді. Бұл құбылыстар тасымалдау құбылыстары делінеді. Осындай құбылыстарға диффузия, жылу өткізгіштік және ішкі үйкеліс құбылыстары жатады.

Диффузия процесінде масса, жылу алмасуда энергия, ішкі үйкелісте импульс тасымалданады. Осы құбылыстың барлығын бір теңдеумен түсіндіруге болады.

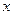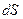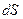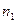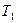
өсіне перпендикуляр болатын ауданын қарастырайық (2.7.1-сурет). ауданның сол жағындағы газ , ,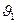, 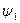ал оң жағы ,,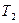 , 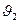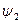параметрлерімен сипатталсын, 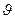- молекулалардың жылдамдығы, -газ молекулаларының концентрациясы (көлем бірлігіндегі молекулалар саны), -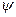

тасымалданатын физикалық шама.

Молекулалардың қозғалысы ретсіз болғандықтан барлық молекулалардың 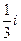-і 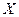өсі бойынша (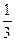-дің жартысы 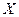өсінің оң бағытында,

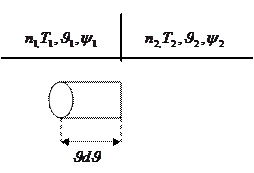
2.7.1 -сурет

ал қалған жартысы 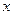өсінің теріс бағытында) қозғалсын дейік. Жасаушысы 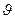dф болатын цилиндрлік бет алып, 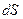ауданы арқылы өтетін ағынды есептейік. Солдан оңға қарай 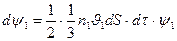, оңнан солға қарай ағыны өтсін. Қорытқы ағын

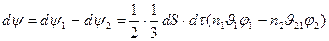(2.7.1)

(2.7.1) теңдік тасымалдау теңдеуі делінеді.

2.7.1 Газдардың диффузиясы

Диффузия процесінде тасымалданушы шама 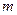масса болады. Ортасы кранмен жалғасқан екі ыдыс алайық. Біреуінде А газ, екіншісінде В газ болсын. (газдар химиялық әсерлесуге түспейді деп есептелсін). Бұл газдардың молекулаларының эффектілік диаметрлері, массалары, жылдамдықтары, еркін қозғалыс жол ұзындығы бірдей болсын. 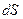ауданы арқылы dф уақыт ішінде диффузияланушы массаны есептейік. (2.7.1.1-сурет). 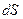ауданы арқылы солдан оңға қарай (не оңнан солға қарай) осы ауданнан қашықтығы еркін қозғалыс жол ұзындығындай аралықтағы молекулалар өтеді. 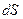ауданынан қашықтығы еркін жол ұзындығынан үлкен болатын қашықтықтағы молекулалар басқа молекулаларға соқтығып, 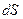ауданынан басқа жаққа ауытқып кетеді.

Тасымалдау теңдеуі бойынша диффузиялаушы масса

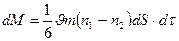(2.7.1.1)

формуласымен анықталады. Бұл формуладағы (n₁-n₂₎ – газ концентрациясының өзгерісі. 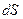ауданының оң және сол жағындағы газ концентрациясының өзгерісі

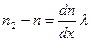және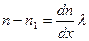

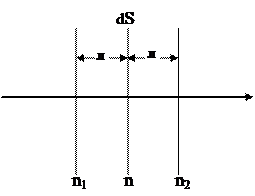
2.7.1.1-сурет

болады. Бұл теңдіктерді қоссақ

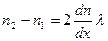(2.7.1.2)

шығады. (2.7.1.2) формуланы (2.7.1.1) формулаға қойған кезде

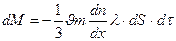(2.7.1.3)

теңдігін аламыз, мұндағы 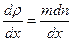– тығыздық градиенті делінеді.

(2.7.1.3) формуланы Фиктің эксперименттік заңымен

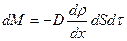
салыстырып

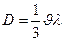(2.7.1.4)

диффузия коэффициентін анықтаймыз, мұндағы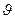-молекулалардың орташа жылдамдығы; 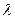-орташа еркін қозғалыс жолының ұзындығы. 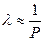, ал 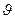қысымға байланысты болмайды, ендеше (2.7.1.4) формула бойынша

байланысы бар.

2.7.2 Газдардағы ішкі үйкелісі

Ньютон заңы бойынша ішкі үйкеліс күші мына формуламен анықталады:

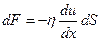(2.7.2.1)

мұндағы 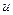– газ қабатының ағыс жылдамдығы; 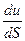– жылдамдық градиенті; 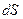газ қабатының арасындағы қабаттасушы аудан.

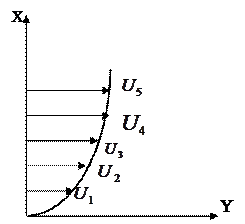
2.7.2.1-сурет

Жылдам қозғалатын қабат баяу қозғалатын қабатқа үдетуші күшпен әсер етеді. Ал баяу қозғалатын қабат жылдам қозғалатын қабатқа тежеулі күшпен әсер етеді (2.7.2.1-сурет). Осы күштерді ішкі үйкеліс күштері дейді.

Көршілес қабаттар бір қабаттан екінші қабатқа импульс беру арқылы әсер етеді. Молекулалық - кинетикалық теория бойынша жылдам қозғалатын қабаттағы молекула баяу қозғалатын қабатқа өткенде үдетуші импульс әкеледі, ал баяу қозғалатын қабаттан жылдам қоғалатын қабатқа өткен молекула тежеуші импульс әкеледі (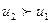). 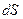ауданы арқылы тасылатын импульсті есептейік. Молекулалар ретсіз жылулық қозғалыста болғандықтан барлық молекулалардың 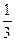-і х-өсі бойынша және осының жартысы солдан оңға қарай (өсінің оң бағыты) қозғалсын (2.7.2.2- сурет).

2.7.2.2-сурет

Барлық молекулалардың жылулық қозғалыс жылдамдықтары мен концентрациялары бірдей болсын делік. 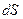ауданы арқылы одан қашықтығы еркін қозғалыс жол ұзындығы л –дан кіші болатын молекулалар өте алады. Молекулалардың таситын шамасы 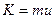импульс. Онда тасымалдау теңдеуі төмендегідей болады:

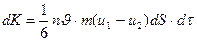(2.7.2.2)

мұнда 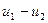- қабаттар аралығындағы жылдамдық өзгерісі. (2.7.2.2) – сурет бойынша 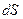ауданынан л қашықтықтағы молекулалардың ағыс жылдамдығының өзгерісі 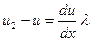және 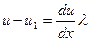болады.

Бұларды бір-біріне қосып

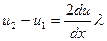(2.7.2.3)

табамыз (2.7.2.3) формуланы (2.7.2.2) формулаға қойсақ:

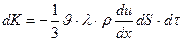(2.7.2.4)

болып шығады.Бұл теңдіктегі 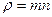- тығыздық., 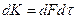импульс өзгерісі. (2.7.2.1)-ні ескерсек

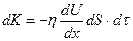(2.7.2.5)

болады. (2.7.2.4) және (2.7.2.5) формулаларды салыстырып

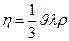(2.7.2.6)

ішкі үйкеліс коэффициентін анықтауға болады. 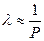, 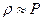болғандықтан з қысымға байланыссыз болады. Мұны былай түсіну керек: қысым P азайғанда көлем бірлігіндегі молекулалар саны n азаяды, бірақ қысымның азаюымен бірге еркін қоғалыс жол ұзындығы артады. Бұл жағдай dS ауданға алыс қабаттағы молекулалардың ешбір соқтығысуға ұшырамастан келуін қамтамасыз етеді.

Бір-біріне қарсы осы екі жағдайдың нәтижесінде бір қабаттан екінші қабатқа тасылатын импульс тұрақты болады. Яғни ішкі үйкеліс коэффициенті з қысымға байланыссыз болады. Бұл жағдай тәжрибелермен дәлелденген.

2.7.3 Газдардың жылу өткізгіштігі

Жылу өткізгіштік құбылысында газдың бір қабатынан екінші қабатына тасылатын шама энергия болады

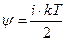
мұндағы i – молекулалардың еркіндік дәреже саны; Т – газ температурасы; 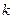– Больцман тұрақтысы.

Газ қабаттарының температурасы Т₁ және Т­₂ болсын (2.7.3.1 – сурет).

Температуралар айырымы

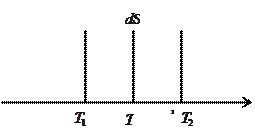
2.7.3.1-сурет

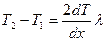(2.7.3.1)

болады. Тасымалдау теңдеуін мына түрде жазамыз:

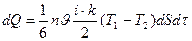(2.7.3.2)

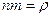(2.7.3.3)

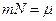, (2.7.3.4)

мұндағы 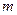- бір молекуланың массасы; концентрациясы; N – Авогадро саны; м- молярлық масса; с – газ тығыздығы.

(2.7.3.3) және (2.7.3.4) формулаларынан

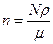(2.7.3.5) 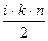өрнегін түрлендірейік. Больцман тұрақтысын 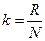және (2.7.3.5)

формуласын пайдаланып

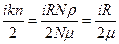
деп жазамыз.

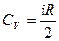– тұрақты көлемдегі молярлық жылу сыйымдылығы; 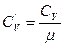– тұрақты көлемдегі меншікті жылу сыйымдылығы. Ендеше

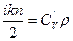(2.7.3.6)

деп жазуға болады.

(2.7.3.2) формулаға (2.7.3.1), (2.7.3.6) –ды қоямыз:

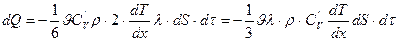(2.7.3.7)

(2.7.3.7) формуланы эксперименттік Фурье заңымен

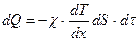
салыстырып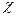 жылу өткізгіштік коэффициентін анықтаймыз:

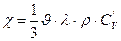(2.7.3.8) (2.7.3.8) формуладағы 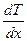- температура градиенті делінеді.

Жылу өткізгіштік коэффициенті 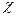қысымға байланыссыз болады, себебі л~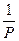және 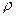~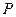. Сонымен қатар орташа жылдамдық 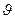және меншікті жылу сыйымдылық С^' _v қысымға байланыссыз болады.

Тасымалдау құбылыстарындағы тасымалданатын шамалар, тасымалдау теңдеулері, тасымалддау коэффициенттері 2- кестеде көрсетілген.

2-кесте

Тасымалданушы шама	Тасымалдау құбылысы	Тасымалдау теңдеуі	Тасымалдау коэффициенті
Газ массасы	Диффузия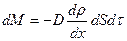
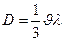
Импульс	Ішкіүйкеліс, тұтқырлық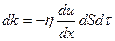
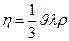
Энергия	Жылу өткізгіштік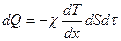

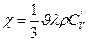
Дата добавления: 2014-10-15