
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электростатика
|
|
|
|
3.1.1 Электр зарядының сақталу заңы. Электр өрісі
Табиғаттағы негізгі әсерлесу күштерінің бірі - электромагниттік күштің өрісі электрлік зарядталған бөлшектердің айналасында пайда болады. Мұндай бөлшектерге электрон, протон, кейбір мезондар жатады. Бұл бөлшектерді зарядтарының типіне байланысты екі түрге бөледі - оң және теріс зарядтар. Зарядталған бөлшектер арасындағы күш өзара тартылыс күші де, өзара тебу күші де болуы мүмкін. Аттас зарядталған бөлшектер бірін-бірі тебеді, ал әр аттас зарядталған бөлшектер біріне - бірі тартылады.
Электр зарядтары дискретті, яғни кез келген денелердің зарядтары бүтін элементар зарядтардан тұрады. Элементар зарядтың шамасы  Кл. Электрон мен протонның зарядтарының таңбалары қарама қарсы, шама жағынан өзара тең және бөлінбейтін ең аз заряд екендігі тәжірибе жүзінде дәлелденген (Милликен тәжірибесі).
Кл. Электрон мен протонның зарядтарының таңбалары қарама қарсы, шама жағынан өзара тең және бөлінбейтін ең аз заряд екендігі тәжірибе жүзінде дәлелденген (Милликен тәжірибесі).
Табиғатта зарядталған бөлшектер жүйесі үшін зарядтардың сақталу заңы орындалады: кез келген тұйықталған жүйеде зарядтардың алгебралық қосындысы өзгермейді.

Электр заряды релятивтік инвариантты, яғни зарядтың шамасы санақ жүйесіне байланысты емес. Ендеше зарядтың шамасы оның қозғалыста немесе тыныштық күйде болуына байланысты емес.
Қозғалмайтын нүктелік зарядтардың әсерлесуін зерттей отырып 1985 жылы Кулон тәжірибе нәтижесінде мынадай заңды ашты: нүктелік екі зарядтың өзара әсерлесу күші әрбір зарядтың шамаларының көбейтіндісіне тура пропорционал және олардың ара қашықтығының квадратына кері пропорционал болады.
Кулон заңы мынадай формула арқылы өрнектеледі
 (3.1.1.1)
(3.1.1.1)
мұндағы 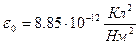 - электрлік тұрақты,
- электрлік тұрақты,  - зарядтар орналасқан ортаның диэлектрлік өтімділігі,
- зарядтар орналасқан ортаның диэлектрлік өтімділігі, 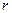 - зарядтардың арақашықтығы,
- зарядтардың арақашықтығы, 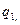 мен
мен  - зарядтардың шамасы.
- зарядтардың шамасы.
Векторлық түрде Кулон заңы былай жазылады
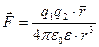 (3.1.1.2)
(3.1.1.2)
(3.1.1.1) - суреттегі 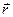 - зарядтарды қосатын радиус – вектор;
- зарядтарды қосатын радиус – вектор; 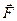 -
- 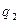 зарядқа
зарядқа 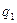 заряд тарапынан әсер етуші күш.
заряд тарапынан әсер етуші күш.
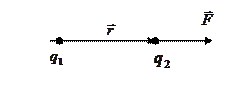
3.1.1.1 – сурет
Нүктелік заряд деп осы дененің электр зарядтарын тасымалдайтын басқа денелерге дейінгі қашықтығымен салыстырғанда мөлшерін ескермеуге болатын зарядталған денені айтады.
Кез келген заряд өзінің айналасында электр өрісін тудырады. Қозғалмайтын зарядталған денелердің немесе бөлшектердің өзаара әсерлесулері материяның бір түрі - электростатикалық өріс арқылы жүзеге асады. Өрісті зерттеу үшін оның әр жерде орналасқан нүктелеріне "сыншы"  зарядты апарсақ, оған әсер етуші күш
зарядты апарсақ, оған әсер етуші күш 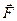 әр жерде түрліше болады және
әр жерде түрліше болады және  қатынасы
қатынасы  шамасына байланысты болмайды. Өріске өзгеріс енгізбеу үшін "сыншы" зарядтың шамасы мейлінше аз болу керек. Электростатикалық өрістің күштік сипаттамасын кернеулік векторы деп атайды.
шамасына байланысты болмайды. Өріске өзгеріс енгізбеу үшін "сыншы" зарядтың шамасы мейлінше аз болу керек. Электростатикалық өрістің күштік сипаттамасын кернеулік векторы деп атайды. 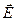 өріс кернеулігінің векторы деп шама жағынан өріс тарапынан бірлік оң “сыншы” зарядқа әсер етуші күшке тең және бағыты күштің әсер ету бағытымен бағыттас физикалық шаманы айтады.
өріс кернеулігінің векторы деп шама жағынан өріс тарапынан бірлік оң “сыншы” зарядқа әсер етуші күшке тең және бағыты күштің әсер ету бағытымен бағыттас физикалық шаманы айтады.
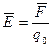 (3. 1.1.3)
(3. 1.1.3)
Электр өрісінде  қозғалмайтын нүктелік зарядқа әсер етуші күш мына формуламен анықталады:
қозғалмайтын нүктелік зарядқа әсер етуші күш мына формуламен анықталады:
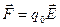 .
.
Нүктелік зарядтың өріс кернеулігін анықтау үшін Кулон заңын пайдалана отырып

деп жазуға болады. Скаляр түрде жазылуы
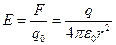 (3.1.1.4)
(3.1.1.4)
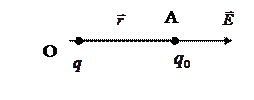
3.1.1.2 – сурет
(3.1.2) - суреттегі 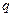 өріс тудырушы заряд, ал
өріс тудырушы заряд, ал  сыншы заряд. Егер өріс тудырушы заряд теріс болса, ("сыншы" заряд әр уақытта оң) онда Ē векторы зарядқа қарай бағытталады (3.1.1.3 – сурет).
сыншы заряд. Егер өріс тудырушы заряд теріс болса, ("сыншы" заряд әр уақытта оң) онда Ē векторы зарядқа қарай бағытталады (3.1.1.3 – сурет).
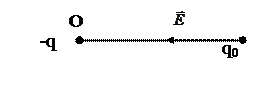
3.1.1.3 – сурет
Халықаралық бірліктер жүйесінде өріс кернеулігінің өлшем бірлігі
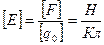 (3.1.1.5)
(3.1.1.5)
Электр өрісінің суперпозиция принципі: Қозғалмайтын нүктелік зарядтар жүйесінің электр өрісінің кернеулігі берілген нүктеде әр зарядтың тудыратын электр өрісінің кернеуліктерінің геометриялық қосындысына тең.
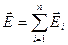 (3.1.1.6)
(3.1.1.6)
Өрістің әр бір нүктесінде кернеулік векторының бағытын және шамасын көрсету арқылы өрісті сипаттауға болады. Егер нүктелік заряд оң болса 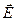 кернеулік сызықтары зарядтан шығатын болады, ал теріс болса зарядқа қарай бағытталған радиалды түзулер болады. (3.1.1.4-сурет)
кернеулік сызықтары зарядтан шығатын болады, ал теріс болса зарядқа қарай бағытталған радиалды түзулер болады. (3.1.1.4-сурет)

3.1.1.4 – сурет
3.1.2 Кернеулік векторының ағыны. Остроградский-Гаусс заңы
Денені нүктелік заряд ретінде қарастыруға мүмкіндік болмаған жағдайларда, оның айналасындағы өрісті Кулон заңын қолданып есептеу өте қиын. Бұл жағдайларда Остроградский-Гаусс заңын қолданған ұтымды. Ол үшін кернеулік ағыны 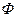 ұғымы кіргізіледі. Кернеулік сызықтарының жиілігі (кернеулік ағыны)
ұғымы кіргізіледі. Кернеулік сызықтарының жиілігі (кернеулік ағыны) 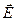 - нің модуліне тең. Тұйық беттің
- нің модуліне тең. Тұйық беттің 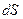 элементар ауданын қиып өтетін сызықтар саны
элементар ауданын қиып өтетін сызықтар саны 
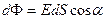 - ға тең болады (3.1.2.1 – сурет).
- ға тең болады (3.1.2.1 – сурет).
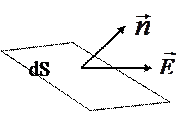
3.1.2.1 – сурет
Сондықтан кез келген тұйық беттен өтетін вектор ағыны
 (3.1.2.1)
(3.1.2.1)
болады, интегралдау тұйық бет арқылы жүргізіледі.
Радиусы r сфералық бетті қиып өтетін нүктелік 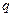 заряды туғызған кернеулік векторының ағынын есептеу керек болсын (3.1.2.2 – сурет).
заряды туғызған кернеулік векторының ағынын есептеу керек болсын (3.1.2.2 – сурет).
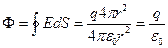 (3.1.2.2)
(3.1.2.2)
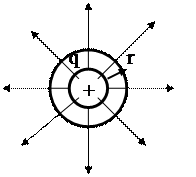
3.1.2.2 – сурет
Егер өрісті 
 зарядтар жүйесі тудыратын болса, онда суперпозиция принципі бойынша
зарядтар жүйесі тудыратын болса, онда суперпозиция принципі бойынша 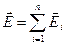 болады. Ендеше кернеулік векторының ағыны
болады. Ендеше кернеулік векторының ағыны
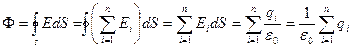 (3.1.2.3)
(3.1.2.3)
Яғни: тұйықталған бет арқылы өтетін электр өрісі кернеулігінің вектор ағыны осы беттің ішінде қоршалған зарядтардың алгебралық қосындасына тең. Бұл тұжырымды Остроградский-Гаусс заңы деп атайды. Егер тұйықталған беттің ішінде ешқандай заряд болмаса, онда бетті қиып өтетін кернеулік векторының ағыны нөлге тең болады.
Гаусс теоремасының қолданылуына бірнеше мысал қарастырайық.
1) Біркелкі зарядталған шексіз жазықтықтың өрісін есептеу (3.1.2.3- сурет).
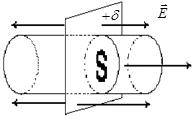
3.1.2.3- сурет
Кернеулік сызықтары жазықтыққа перпендикуляр және жазықтықтан екі жаққа қарай бағытталады. Тұйық бет үшін жасаушысы жазықтыққа перпендикуляр, ал табаны S жазықтыққа параллель орналасқан симметриялы цилиндрлік бет жүргізейік. Цилиндрдің бүйір беті арқылы өтетін ағын нөлге тең, өйткені цилиндр жасаушыcы ағын сызықтарына параллель. Сонымен, толық ағын цилиндр табандары арқылы өтетін ағындардың қосындысы  -ке тең болады. Цилиндр беті ішіндегі заряд
-ке тең болады. Цилиндр беті ішіндегі заряд 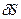 . Гаус теоремасы бойынша
. Гаус теоремасы бойынша
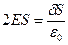 (3.1.2.4)
(3.1.2.4)
бұл өрнектен 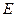 - ні анықтауға болады.
- ні анықтауға болады.
 (3.1.2.5)
(3.1.2.5)
2) Әр аттас зарядталған параллель екі шексіз жазықтықтың өрісін есептеу.
Беттік тығыздықтарды 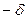 және
және  болатын екі параллель шексіз жазықтықтардың өрісін әрбір жазықтық тудыратын өрістердің суперпозициясы ретінде қарастыруға болады. (3.2.4 –сурет)
болатын екі параллель шексіз жазықтықтардың өрісін әрбір жазықтық тудыратын өрістердің суперпозициясы ретінде қарастыруға болады. (3.2.4 –сурет)
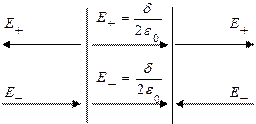
3.1.2.4 –сурет
Жазықтықтар арасындағы аймақта кернеулік сызықтары бағыттас болғандықтан қорытқы кернеулік
 (3.1.2.6)
(3.1.2.6)
ал, жазықтықпен шектелген көлемнен тыс жерде қосылатын өрістердің бағыттары қарама - қарсы, ендеше қорытқы кернеулік нөлге тең.
3) Біркелкі зарядталған сфералық беттің өрісін есептеу.
Радиусы 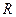 сфералық бет
сфералық бет 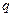 зарядпен зарядталсын (3.1.2.5 – сурет).
зарядпен зарядталсын (3.1.2.5 – сурет).

3.1.2.5 – сурет
Өрістің 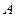 нүктесіндегі кернеулігі Гаусс теоремасы бойынша анықталады.
нүктесіндегі кернеулігі Гаусс теоремасы бойынша анықталады.
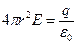 (3.1.2.7)
(3.1.2.7)
Бұл өрнектен кернеулікті анықтауға болады:
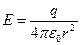 (3.1.2.8)
(3.1.2.8)
 нүктесінде
нүктесінде  болғандықтан,
болғандықтан,  болады, өйткені радиусы
болады, өйткені радиусы  тұйық бет ішінде заряд нөлге тең.
тұйық бет ішінде заряд нөлге тең.
4) Көлемдік зарядталған сфераның өрісі.
Радиусы 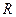 заряды
заряды 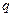 сфера берілсін. Сонда көлемдік тығыздығы
сфера берілсін. Сонда көлемдік тығыздығы
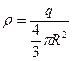 (3.1.2.9)
(3.1.2.9)
болады. Сфераның сыртындағы (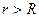 ) өріс кернеулігі (3.1.2.8) формуласымен анықталады. Ал сфераның ішіндегі (
) өріс кернеулігі (3.1.2.8) формуласымен анықталады. Ал сфераның ішіндегі ( ) өріс кернеулігі Гаус теоремасы бойынша
) өріс кернеулігі Гаус теоремасы бойынша
 (3.1.2.10)
(3.1.2.10)
(3.1.2.9) формуласын ескерген жағдайда
 (3.1.2.11)
(3.1.2.11)
болып шығады.
5) Біркелкі зарядталған шексіз цилиндрлік беттің өрісін есептеу.
Радиусы R шексіз цилиндр сызықтық тығыздығы  зарядпен біркелкі зарядталған болсын (3.1.2.6 – сурет).
зарядпен біркелкі зарядталған болсын (3.1.2.6 – сурет).
Симметрия тұрғысынан кернеулік сызықтары бетке перпендикуляр болатын радиал сызықтар болады. Цилиндр өсінен 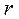 қашықтықтағы өріс кернеулігін анықтайық. Ол үшін ұзындығы
қашықтықтағы өріс кернеулігін анықтайық. Ол үшін ұзындығы 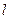 , радиусы
, радиусы 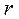 болатын каокциалды цилиндрлік бет тұрғызайық. Осы бет арқылы өтетін Ē кернеулік ағыны
болатын каокциалды цилиндрлік бет тұрғызайық. Осы бет арқылы өтетін Ē кернеулік ағыны 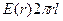 болады.
болады.
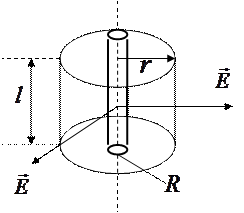
3.1.2.6 – сурет
Гаусс теоремасы бойынша, 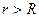 болғанда
болғанда
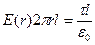 (3.1.2.12)
(3.1.2.12)
бұдан
 (3.1.2.13)
(3.1.2.13)
Егер 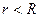 болған жағдайда, онда қарастырылатын тұйық беттің ішінде заряд болмайды, ендеше
болған жағдайда, онда қарастырылатын тұйық беттің ішінде заряд болмайды, ендеше
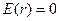 (3.1.2.14)
(3.1.2.14)
болады.
3.1.3 Электростатикалық өріс күштерінің жұмысы. Потенциал
Қозғалмайтын заряд 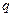 -дің өрісінде
-дің өрісінде 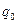 зарядын
зарядын 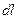 қашықтыққа апарғанда істелетін жұмыс мынаған тең:
қашықтыққа апарғанда істелетін жұмыс мынаған тең:
 (3.1.3.1)
(3.1.3.1)
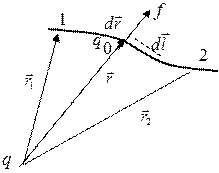
3.1.3.1 – сурет
Сурет бойынша 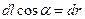 -ға тең.. Онда
-ға тең.. Онда
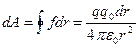 (3.1.3.2)
(3.1.3.2)
Осыдан 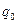 зарядты 1-ші нүктеден 2-ші нүктеге апарғанда істелетін жұмысты анықтауға болады.
зарядты 1-ші нүктеден 2-ші нүктеге апарғанда істелетін жұмысты анықтауға болады.
 (3.1.3.3)
(3.1.3.3)
(3.1.3.3) формуладан 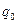 заряды тудырған өрісінің күшінің істейтін жұмысы зарядтың орын ауыстыратын жолына байланысты емес, тек бастапқы және соңғы орындарына ғана байланысты екендігі көрінеді.. Мұндай күштерді потенциалық күштер дейді. Потенциалық күштердің тұйық жолда істейтін жұмысы нөлге тең болады.
заряды тудырған өрісінің күшінің істейтін жұмысы зарядтың орын ауыстыратын жолына байланысты емес, тек бастапқы және соңғы орындарына ғана байланысты екендігі көрінеді.. Мұндай күштерді потенциалық күштер дейді. Потенциалық күштердің тұйық жолда істейтін жұмысы нөлге тең болады.
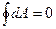 (3.1.3.4)
(3.1.3.4)
Потенциалдық күш өрісіндегі заряд 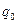 орын ауыстырғанда істелетін жұмыс
орын ауыстырғанда істелетін жұмыс 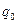 зарядтың бастапқы және соңғы орындарындағы потенциялық энергияларының айырмасына тең болады.
зарядтың бастапқы және соңғы орындарындағы потенциялық энергияларының айырмасына тең болады.
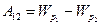 (3.1.3.5)
(3.1.3.5)
мұндағы
 (3.1.3.6)
(3.1.3.6)
бастапқы және соңғы орындарындағы 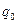 зарядтың потенциялық энергиялары. Потенциялық энергия электростатикалық өрістің бір нүктесіне орналастырылған зарядталған бөлшекке өрістің әсерін сипаттайды. Сонымен электростатикалық өріс – потенциалдық өріс.
зарядтың потенциялық энергиялары. Потенциялық энергия электростатикалық өрістің бір нүктесіне орналастырылған зарядталған бөлшекке өрістің әсерін сипаттайды. Сонымен электростатикалық өріс – потенциалдық өріс.
Нүктелік зарядтар жүйесі 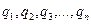 зарядтардан тұрса, онда суперпозиция принципі бойынша жүйенің потенциялдық энергиясы
зарядтардан тұрса, онда суперпозиция принципі бойынша жүйенің потенциялдық энергиясы
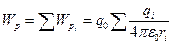 (3.1.3.7)
(3.1.3.7)
формуласымен анықталады. Осы формула бойынша электростатикалық өріс потенциялын анықтауға болады
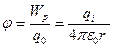 (3.1.3.8)
(3.1.3.8)
Берілген нүктедегі өрісті энергия тұрғысынан сипаттайтын шама өріс потенциалы деп аталады.
(3.1.3.5), (3.1.3.7) және (3.1.3.8) формулаларынан электростатикалық өрістің жұмысы  заряд пен потенциалдар айырмасының көбейтіндісіне тең болатындығы шығады.
заряд пен потенциалдар айырмасының көбейтіндісіне тең болатындығы шығады.
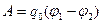 (3.1.3.9)
(3.1.3.9)
Екінші жағынан 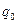 зарядты өрістің 1-ші нүктесінен 2-ші нүктесіне тасымалдану жұмысы былай жазылады
зарядты өрістің 1-ші нүктесінен 2-ші нүктесіне тасымалдану жұмысы былай жазылады
 (3.1.3.10)
(3.1.3.10)
(3.1.3.9) және (3.1.3.10) формулаларын салыстыратын болсақ
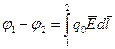 (3.1.3.11)
(3.1.3.11)
екендігі шығады.
Электр өрісінде 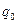 зарядты
зарядты 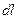 қашықтыққа апарғанда істелетін жұмыс
қашықтыққа апарғанда істелетін жұмыс
 (3.1.3.12)
(3.1.3.12)
Екіншіден (3.1.3.9) формуласы бойынша
 (3.1.3.13)
(3.1.3.13)
осы формулалардан келесі формула шығады
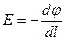 (3.1.3.14)
(3.1.3.14)
Өріс потенциалының ең тез өзгеретін бағыты бойынша туындысы потенциал градиенті делінеді.
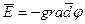 (3.1.3.15)
(3.1.3.15)
Минус (-) таңбасы кернеулік векторының бағыты потенциалдың кемуіне қарай бағытталғандығын көрсетеді.
Потенциялдары бірдей нүктелер жиыны эквипотенциал бет деп аталады. Мысалы, нүктелік зарядтың айналасындағы эквипотенциал беттер концентрлі шеңберлер болады.
3.1.4 Диэлектриктер. Диэлектриктердегі поляризация құбылысы
Өткізгіштер деп ішінде өзара байланысты емес, еркін қозғала алатын зарядталған бос бөлшектері бар денелерді айтады. Диэлектриктер деп, керісінше, бойында зарядталған бос бөлшектері болмайтын денелерді айтады. Диэлектриктер кез келген заттар сияқты атомдардан және молекулалардан тұрады. Атомдардың оң зарядтары атом ядросында, ал теріс зарядтар атомның электрондық қабықшаларында орналасады. Осы зарядтардың ауырлық центрлерінің орналасуына сәйкес диэлектриктер бірнеше түрге бөлінеді.
Диэлектриктердің бірінші тобына 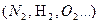 молекулаларының құрылысы симметриялы болатын заттар жатады. Оларды полярсыз диэлектриктер деп атайды. Сыртқы электр өрісі жоқ кезде оң және теріс зарядтардың ауырлық центрлері бір - біріне дәл келетін молекулалар тобын полярсыз молекулалар деп атайды. Сыртқы электр өрісінің әсерінен полярсыз молекулалардың зарядтары қарама - қарсы жаққа (оң зарядтары өріс бойынша, теріс зарядтары өріске қарсы) ығысады.
молекулаларының құрылысы симметриялы болатын заттар жатады. Оларды полярсыз диэлектриктер деп атайды. Сыртқы электр өрісі жоқ кезде оң және теріс зарядтардың ауырлық центрлері бір - біріне дәл келетін молекулалар тобын полярсыз молекулалар деп атайды. Сыртқы электр өрісінің әсерінен полярсыз молекулалардың зарядтары қарама - қарсы жаққа (оң зарядтары өріс бойынша, теріс зарядтары өріске қарсы) ығысады.
Диэлектриктердің екінші тобына  молекулаларының құрылысы ассиметриялы болатын заттар жатады, оларды полярлы диэлектриктер деп атайды. Яғни, оң және теріс зарядтардың ауырлық центрлері бір-біріне дәл келмейді (полярлы молекулалар). Мұндай молекулалардың сыртқы өріс болмаған жағдайда
молекулаларының құрылысы ассиметриялы болатын заттар жатады, оларды полярлы диэлектриктер деп атайды. Яғни, оң және теріс зарядтардың ауырлық центрлері бір-біріне дәл келмейді (полярлы молекулалар). Мұндай молекулалардың сыртқы өріс болмаған жағдайда
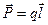 (3.1.4.1)
(3.1.4.1)
дипольдық моменті болады (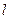 -зарядтардың ара қашықтығы), бірақ жылулық қозғалыс салдарынан кеңістікте ретсіз орналасады. Ал өріс әсер еткен жағдайда дипольдың оң зарядты жағы электр өрісінің бағытына қарай, теріс зарядты жағы өріске қарсы болатындай орналасады.
-зарядтардың ара қашықтығы), бірақ жылулық қозғалыс салдарынан кеңістікте ретсіз орналасады. Ал өріс әсер еткен жағдайда дипольдың оң зарядты жағы электр өрісінің бағытына қарай, теріс зарядты жағы өріске қарсы болатындай орналасады.
Диэлектриктердің үшінші тобына ( ) молекулаларының құрылысы ионды болатын заттар жатады. Иондық кристалдар оң және теріс иондар дұрыс кезектесіп отыратын кеңістік торлардан тұрады. Сыртқы электр өрісі әсер еткенде кристалдық тор деформацияланады, ал бұл жағдай дипольдық моментің пайда болуына әкеледі.
) молекулаларының құрылысы ионды болатын заттар жатады. Иондық кристалдар оң және теріс иондар дұрыс кезектесіп отыратын кеңістік торлардан тұрады. Сыртқы электр өрісі әсер еткенде кристалдық тор деформацияланады, ал бұл жағдай дипольдық моментің пайда болуына әкеледі.
Диэлектриктердің байланысқан оң және теріс зарядтарының қарама - қарсы жаққа қарай ығысуын поляризация құбылысы деп атайды. Поляризация құбылысының салдарынан диэлектриктің ішінде сыртқы өріске қарама-қарсы бағытталған өріс пайда болады. Диэлектрик ішіндегі өрістің әр кезде сыртқы өрістен әлсіз болуының себебі де осыдан.
Қарастырылған диэлектриктердің үш тобына сәйкес поляризация құбылысы үш түрге бөлінеді. Біріншісі электрондық, екіншісі дипольдық, үшіншісі иондық поляризация делінеді.
Электрондық поляризацияда полярсыз молекулалардың атомдарында өрістің әсерінен дипольдық моменттер пайда болады, яғни электрондардың орбиталары деформацияланады.
Дипольдық поляризацияда полярлы молекулалардағы дипольдық моменттері бар молекулалар өріс бойынша ығысады.
Иондық поляризацияда кристалдық тордағы оң иондар өріс бойынша, теріс иондар өріске қарсы ығысады.
Сыртқы электр өрісінің салдарынан диэлектрик поляризацияланады да, дипольдық момент пайда болады.
 (3.1.4.2)
(3.1.4.2)
мұндағы  - бір молекуланың дипольдық моменті. Диэлектриктің поляризациялану дәрежесін сипаттау үшін поляризациялану шамасы енгізіледі.
- бір молекуланың дипольдық моменті. Диэлектриктің поляризациялану дәрежесін сипаттау үшін поляризациялану шамасы енгізіледі.
 (3.1.4.3)
(3.1.4.3)
мұндағы 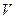 - көлем,
- көлем, 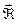 - поляризациялану векторы делінеді.
- поляризациялану векторы делінеді.
Диэлектриктердің (сегнетоэлекриктерден басқа) поляризациялану векторы мен кернеулік векторының арасындағы байланыс
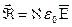 (3.1.4.4)
(3.1.4.4)
формуласымен беріледі, мұндағы 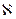 - поляризация коэффиценті делінеді.
- поляризация коэффиценті делінеді.
Әр аттас зарядталған шексіз екі параллель пластинкалар арасына диэлектриктер орналастырылсын (3.1.4.1 – сурет).

3.1.4.1 – сурет
Электр өрісінің салдарынан диэлектрик поляризацияланады да, оның бетінде тығыздығы  байланысқан зарядтар пайда болады. Диэлектрик ішінде кернеулігі
байланысқан зарядтар пайда болады. Диэлектрик ішінде кернеулігі
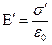 (3.1.4.5)
(3.1.4.5)
болатын өріс пайда болады. Диэлектрик жоқ жердегі өрістің кернеулігі
 (3.1.4.6)
(3.1.4.6)
Бұл өрістер қарама - қарсы бағытталған. Сондықтан диэлектрик ішіндегі кернеулік
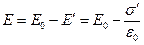 (3.1.4.7)
(3.1.4.7)
Диэлектриктерден тыс жерде 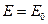 болады.
болады.
Байланысқан зарядтардың беттік тығыздығын анықтайық. Ол үшін электр өрісіндегі диэлектриктен ұзындығы  , электр өрісіне параллель болатын цилиндр бөліп алайық (3.1.4.2 – сурет). Сыртқы электр өрісінің әсерінен пайда болатын, цилиндр табандарындағы байланысқан зарядтардың шамасы
, электр өрісіне параллель болатын цилиндр бөліп алайық (3.1.4.2 – сурет). Сыртқы электр өрісінің әсерінен пайда болатын, цилиндр табандарындағы байланысқан зарядтардың шамасы  және
және  болады.
болады.
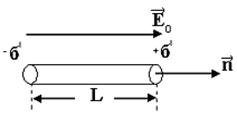
3.1.4.2 – сурет
Осы цилиндрді дипольдық моменті  - ге тең диполь деп қарастырған жағдайда (3.1.4.4) формуласы бойынша поляризация векторы
- ге тең диполь деп қарастырған жағдайда (3.1.4.4) формуласы бойынша поляризация векторы
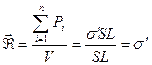 (3.1.4.8)
(3.1.4.8)
болады, яғни поляризациялану векторы байланысқан беттік заряд тығыздығына тең болады.
Егер (3.1.4.7) формуласына (3.1.4.8) және (3.1.4.4) формулаларын қойсақ
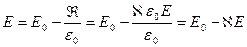 (3.1.4.9)
(3.1.4.9)
бұдан
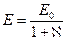 (3.1.4.10)
(3.1.4.10)
екендігі шығады.
Ортаның диэлектрлік өтімділігі  біртекті диэлектрик ішіндегі электр өрісінің кернеулігінің вакуумдегі электр орісінің кернеулігінен неше есе кем екенігін көрсететін физикалық шама
біртекті диэлектрик ішіндегі электр өрісінің кернеулігінің вакуумдегі электр орісінің кернеулігінен неше есе кем екенігін көрсететін физикалық шама
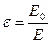 ,
,
ендеше
 (3.14.11)
(3.14.11)
(3.1.4.10) және (3.1.4.11) формулаларынан
 (3.1.4.12)
(3.1.4.12)
 мен
мен 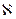 арасындағы байланысты шығарып алуға болады.
арасындағы байланысты шығарып алуға болады.
Электрлік индукция векторы
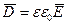 (3.1.4.13)
(3.1.4.13)
формуласымен анықталады. Осыған (3.1.4.12) формуланы қойып және (3.1.4.1) формуланы ескерсек, онда
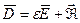 (3.1.4.14)
(3.1.4.14)
байланысын табамыз.
 Электрлік индукция векторының физикалық мағынасын қарастырайық. Диэлектриктегі байланысқан зарядтар бос зарядтар тудыратын сыртқы өріс әсерінен пайда болады және байланысқан зарядтардың кернеулігі мен сыртқы өріс кернеулігі қосылады. Сонымен диэлектриктегі қорытқы өріс кернеулігі Ē векторымен анықталады. Ē векторы диэлектриктің
Электрлік индукция векторының физикалық мағынасын қарастырайық. Диэлектриктегі байланысқан зарядтар бос зарядтар тудыратын сыртқы өріс әсерінен пайда болады және байланысқан зарядтардың кернеулігі мен сыртқы өріс кернеулігі қосылады. Сонымен диэлектриктегі қорытқы өріс кернеулігі Ē векторымен анықталады. Ē векторы диэлектриктің  қасиетіне байланысты, ал
қасиетіне байланысты, ал  векторы ортаның
векторы ортаның  қасиетіне байланыссыз. Ендеше
қасиетіне байланыссыз. Ендеше  векторы еркін зарядтар тудыратын электростатикалық өрісті сипаттайды. Шынында (3.1.4.13) формуласын (3.1.4.11) формуласына қоятын болса
векторы еркін зарядтар тудыратын электростатикалық өрісті сипаттайды. Шынында (3.1.4.13) формуласын (3.1.4.11) формуласына қоятын болса
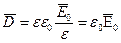 (3.1.4.15)
(3.1.4.15)
болып шығады. Бірақ диэлектрикте пайда болған поляризацияланған (байланысқан) зарядтар өріс тудырушы еркін зарядтардың орналасуын өзгертеді. Сонымен  векторы диэлектрик бар кездегі еркін зарядтардың тудыратын өріс кернеулігін сипаттайды.
векторы диэлектрик бар кездегі еркін зарядтардың тудыратын өріс кернеулігін сипаттайды.
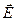 векторының сызықтары кез келген зарядтардан басталып (байланысқан және еркін) және аяқталады. Ал
векторының сызықтары кез келген зарядтардан басталып (байланысқан және еркін) және аяқталады. Ал 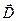 векторы тек еркін зарядтардан басталып және аяқталады.
векторы тек еркін зарядтардан басталып және аяқталады.
 векторы үшін Гаус теоремасы
векторы үшін Гаус теоремасы
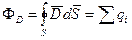 (3.1.4.16)
(3.1.4.16)
ал, 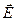 векторы үшін Гаус теоремасы былай жазылады
векторы үшін Гаус теоремасы былай жазылады
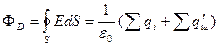 (3.1.4.17)
(3.1.4.17)
мұндағы 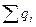 және
және  еркін және поляризацияланған зарядтардың қосындысы.
еркін және поляризацияланған зарядтардың қосындысы.
Кейбір диэлектриктер белгілі бір температуралар аралығында өздігінен (спонтанды) поляризацияланады. Мұндай жағдай алғаш рет сегнет тұзында байқалды. Сондықтан осыған ұқсас барлық заттар сегнетоэлекриктер деп аталады. Сегнетоэлектриктердің диэлектрлік өтімділігі өте жоғары (мысалы, сегент тұзы үшін 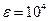 ) және өріс кернеулігіне байланысты болады. Сегнетоэлектриктер үшін (3.1.4.1) формуласы дұрыс болмайды.
) және өріс кернеулігіне байланысты болады. Сегнетоэлектриктер үшін (3.1.4.1) формуласы дұрыс болмайды.
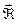 поляризациялану векторы мен
поляризациялану векторы мен 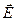 кернеулік векторлары арасындағы байланысты қарастырайық (3.1.4.3. – сурет).
кернеулік векторлары арасындағы байланысты қарастырайық (3.1.4.3. – сурет).
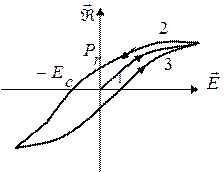
3.1.4.3 – сурет
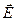 сыртқы кернеулік вектор өскенде
сыртқы кернеулік вектор өскенде 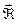 поляризация векторы да өседі (3.1.4.3 - суреттегі 1 – қисық).
поляризация векторы да өседі (3.1.4.3 - суреттегі 1 – қисық). 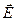 - нің кемуіне сәйкес
- нің кемуіне сәйкес 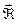 - нің кемуі 2 - қисық бойынша жүреді. Суретте
- нің кемуі 2 - қисық бойынша жүреді. Суретте  болғанда
болғанда 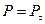 екендігі көрінеді..
екендігі көрінеді.. 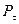 - қалдық поляризация делінеді. Қалдық поляризацияны жою үшін сыртқы өріс бағытын өзгерту керек.
- қалдық поляризация делінеді. Қалдық поляризацияны жою үшін сыртқы өріс бағытын өзгерту керек. 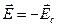 болғанда
болғанда  болады.
болады. 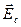 - коэрцитивтік күш делінеді.
- коэрцитивтік күш делінеді. 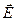 - нің одан әрі өзгерісі З - қисық бойынша өтіп, қисық тұйықталады. Мұны гистерезис тұзағы деп атайды.
- нің одан әрі өзгерісі З - қисық бойынша өтіп, қисық тұйықталады. Мұны гистерезис тұзағы деп атайды.
Әрбір сегнетоэлектриктің өзіне тән температурасы болады, бұдан жоғары температурада зат өзінің ерекше қасиетін жоғалтады да, сегнетоэлекрик кәдімгі диэлектрикке айналады. Бұл температура Кюри нүктесі делінеді. Сегнетоэлектриктерде бір ғана Кюри нүктесі болады. Тек сегнет тұзы және оның изоморфты қосылыстарында ғана екі Кюри нүктесі (-18 және +240С) болады.
3.1.5 Электростатикалық өрістегі өткізгіштер
Өткізгіштерді электр өрісіне апарып орналастырса өткізгіштің бос зарядтары қозғала бастайды да, бұл қозғалыс өткізгіш ішіндегі электорстатикалық өріс нөлге тең болғанға дейін тоқталмайды. Қозғалыс уақыты өте қысқа болады. (секундтық үлес ішінде).
Өткізгіш ішінің барлық жеріндегі өріс кернеулігі нөлге тең болады.
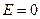 (3.1.5.1)
(3.1.5.1)
және өткізгіш бетінің әр бір нүктесіндегі өріс кернеулігі бетке жүргізілген нормаль бойымен бағытталған болуы керек:
 (3.1.5.2)
(3.1.5.2)
Яғни тепе - теңдік жағдайда өткізгіш беті эквипотенциалды болады. Өткізгішке заряд берілсе ол өткізгіш бетіне орналасады.
Өткізгіш беті маңындағы кернеулік 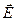 пен өткізгіш бетіндегі
пен өткізгіш бетіндегі 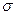 беттік заряд тығыздығының арасындағы байланысты қарастырайық. Ол үшін табаны
беттік заряд тығыздығының арасындағы байланысты қарастырайық. Ол үшін табаны 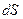 болатын цилиндрді алайық. Цилиндрдің жартысы өткізгіш сыртында, ал қалған жартысы өткізгіш ішінде орналассын (3.1.5.1 – сурет).
болатын цилиндрді алайық. Цилиндрдің жартысы өткізгіш сыртында, ал қалған жартысы өткізгіш ішінде орналассын (3.1.5.1 – сурет).

3.1.5.1 – сурет
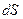 бет арқылы өтетін индукция векторының ағыны
бет арқылы өтетін индукция векторының ағыны 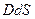 -ке тең. Гаусс теоремасы бойынша бұл ағын
-ке тең. Гаусс теоремасы бойынша бұл ағын  өрнегімен есептелетін заряд шамасына тең. Ендеше,
өрнегімен есептелетін заряд шамасына тең. Ендеше,
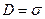 (3.1.5.3)
(3.1.5.3)
Электрлік индукция векторының формуласын қолданып, осы өткізгіш беті маңындағы өріс кернеулігін анықтауға болады.
 (3.1.5.4)
(3.1.5.4)
Егер зарядталмаған өткізгішті электр өрісіне әкеліп қойса, онда оң зарядтар өріс бағытымен, ал теріс зарядтар өріс бағытына қарсы қозғала бастайды (3.1.5.2 – сурет).

3.1.5.2 – сурет
Нәтижесінде өткізгіштің бір жағында индукцияланған оң зарядтар, ал екінші жағында теріс зарядтар пайда болады. Бұл процесс өткізгіш ішіндегі кернеулік 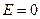 болғанға дейін жүреді. Яғни, электр өрісіне енгізілген бейтарап өткізгіш кернеулік сызықтарының біраз бөлігін үзеді, олар индукцияланған теріс зарядтарға келіп бітеді де оң зарядтардан қайта басталады. Индукцияланған зарядтар өткізгіштің сыртқы бетінде орналасады. Сыртқы өріс әсерінен өткізгіштердің сыртқы бетінде зарядтардың пайда болу құбылысы электростатикалық индукция делінеді.
болғанға дейін жүреді. Яғни, электр өрісіне енгізілген бейтарап өткізгіш кернеулік сызықтарының біраз бөлігін үзеді, олар индукцияланған теріс зарядтарға келіп бітеді де оң зарядтардан қайта басталады. Индукцияланған зарядтар өткізгіштің сыртқы бетінде орналасады. Сыртқы өріс әсерінен өткізгіштердің сыртқы бетінде зарядтардың пайда болу құбылысы электростатикалық индукция делінеді.
Өткізгіш ішінде өрістің болмауы электростатикалық қорғаныс жасауға мүмкіндік тудырады. Электр өрісінен сезімтал приборларды қорғау үшін оларды металл жәшік не металл тор ішіне орналастырады.
Жоғары вольтті электростатикалық генератор зарядтардың өткізгіштің сыртқы бетінде орналасу қасиетіне негізделіп жасалынады. Ван-де-Грааф генераторының құрылысы төмендегідей. Іші қуыс металл шар (1) изоляцияланған тиянаққа (2) орнатылады. Шардың ішінде ұзын резинамен қапталған тоқыма лента (3) айналыста болады (3.1.5.4 - сурет).

3.1.5.4 – сурет
Лентаның жанына жоғары вольтті кернеумен қосылған тарақ (4) орнатылады.. Осы тарақтан зарядтар лентаға беріліп отырады. Пластина (5) зарядтың тарақ арқылы лентаға өтуін арттырады. Зарядтар лентадан түтік (6) арқылы шарға беріліп отырады. Соның нәтижесінде шарды шамасы өте жоғары зарядпен зарядтауға болады (потенциялдар айырмасы бірнеше миллион вольт болады). Ван-де-Граф генераторы зарядталған бөлшектерді үдеткіштер ретінде пайданылады.
3.1.6 Электр сыйымдылығы. Конденсаторлар
Оқшауланған зарядталған өткізгіштің айналасындағы өрістің потенциалы мен өткізгіш бойындағы заряд арасында тура пропорционалдық байланыс бар
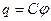
мұндағы 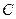 өткізгіштің электр сыйымдылығы деп аталады. Ол өткізгіштің өлшемдері мен формасына және ортаның диэлектриктік өтімділігіне тәуелді.
өткізгіштің электр сыйымдылығы деп аталады. Ол өткізгіштің өлшемдері мен формасына және ортаның диэлектриктік өтімділігіне тәуелді.
Оңашаланған өткізгіштің электр сыйымдылығы
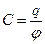 (3.1.6.1)
(3.1.6.1)
Радиусы R зарядталған шардың потенциялы
 (3.1.6.2)
(3.1.6.2)
болады, ендеше шардың электросыйымдылығы
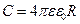 (3.1.6.3)
(3.1.6.3)
Электр сыйымдылықтың өлшем бірлігіне Халықаралық бірліктер жүйесінде Фарад (Ф) алынады.

 (3.1.6.4)
(3.1.6.4)
Фарад өте үлкен өлшем болып табылады. Сондықтар практикада микрофарад, пикофарад өлшемдері қолданылады.
1) Жазық конденсаторлар.
Өзара диэлектрик қабатпен екі өткізгіш астарлардан тұратын жүйені конденсатор деп атайды. Конденсатор астарлары қарама-қарсы таңбалы зарядтармен зарядталады. Конденсатордың астарларының арасындағы потенциалдар айырымы 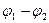 болса, осы конденсатордың сыйымдылығы
болса, осы конденсатордың сыйымдылығы
 (3.1,6.5)
(3.1,6.5)

3.1.6.1 – сурет
Конденсатордың астарларының ауданы 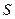 , зарядының шамасы
, зарядының шамасы 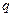 болса, онда астарлар арасындағы кернеулік
болса, онда астарлар арасындағы кернеулік
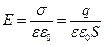 (3.1.6.6)
(3.1.6.6)
Конденсатор астарларының потенциялдар айырымы мен өріс кернеулігі арасындағы байланыс
 (3.1.6.7)
(3.1.6.7)
формуласымен беріледі. (3.1.6.6) формуласын ескерген жағдайда
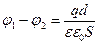 (3.1.6.8)
(3.1.6.8)
(3.1.6.8) формуланы (3.1.6.5)-ке қойып
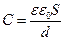 (3.1.6.9)
(3.1.6.9)
жазық конденсатордың электр сыйымдылығының формуласын алуға болады.
2) Сфералық конденсаторлар.
Сфералық конденсатор радиустары 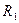 және
және 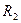 болатын екі концентрлі сфералық беттерден (астарлардан) тұрады. Бұл беттердің арасы диэлектрлік өтімділігі
болатын екі концентрлі сфералық беттерден (астарлардан) тұрады. Бұл беттердің арасы диэлектрлік өтімділігі  болатын диэлектрикпен толтырылады. Астарлардың зарядтары
болатын диэлектрикпен толтырылады. Астарлардың зарядтары  және
және 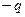 , ал потенциялдары
, ал потенциялдары 
 және
және  болады.
болады.
Сфералық беттің кернеулігі (3.1.2.8) формуласы бойынша
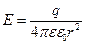 (3.1.6.10)
(3.1.6.10)
Екінші жағынан кернеулік (3.1.3.14) формуласы бойынша
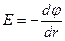 (3.1.6.11)
(3.1.6.11)
(3.1.6.10) және (3.1.6.11) формулаларын қолданғанда төмендегідей өрнек шығады
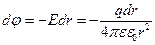 (3.1.6.12)
(3.1.6.12)
Конденсатор астарларының арасындағы потенциалдар айырмасын интегралдау жолымен табуға болады
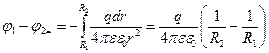 (3.1.6.13)
(3.1.6.13)
(3.1.6.13) формула (3.1.6.5) формулаға қойып
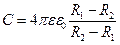 (3.1.6.14)
(3.1.6.14)
сфералық конденсатордың сыйымдылығының формуласын алуға болады.
3) Цилиндрлік конденсаторлар.
Цилиндрлік конденсатор радиустары  және
және 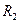 болатын іштері қуыс каоксиалды цилиндрлерден тұрады. Цилиндрлердің арасы диэлектрлік өтімділігі
болатын іштері қуыс каоксиалды цилиндрлерден тұрады. Цилиндрлердің арасы диэлектрлік өтімділігі  болатын диэлектрикпен толтырылған. Астарларындағы зарядтар
болатын диэлектрикпен толтырылған. Астарларындағы зарядтар  және
және 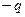 , астарлардың потенциялдары
, астарлардың потенциялдары  және
және  болсын. Астарлардың арасындағы өріс кернеулігі (3.1.2.13) формуласы бойынша
болсын. Астарлардың арасындағы өріс кернеулігі (3.1.2.13) формуласы бойынша

және екіншіден 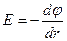
Ендеше осы формулалардан
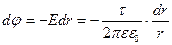 (3.1.6.15)
(3.1.6.15)
Сонда цилиндрлік конденсаторлардың астарларының потенциалдар айырмасы
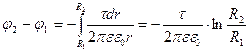 (3.1.6.16)
(3.1.6.16)
Сонымен цилиндрлік конденсатордың сыйымдылығының формуласын шығарып алуға болады.
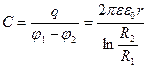 (3.1.6.17)
(3.1.6.17)
4) Әртүрлі диэлектрик қабаттары бар жазық конденсатор
Жазық конденсатордың астарларының арасы диэлектрлік өтімділіктеі 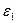 ,
,  және қалыңдықтары
және қалыңдықтары 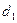 ,
,  болатын диэлектриктермен толтырылсын.
болатын диэлектриктермен толтырылсын.

3.1.6.2 – сурет
Жазық конденсатор сыйымдылығының формуласы
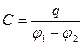
Диэлектриктердегі кернеулік (3.1.4.11) формуласы бойынша
 және
және 
мұндағы  бостықтағы өріс кернеулігі. Бір астардағы зарядтың шамасы
бостықтағы өріс кернеулігі. Бір астардағы зарядтың шамасы
 (3.1.6.18)
(3.1.6.18)
Екі диэлектрик шекарасындағы потенциалды  деп белгілегенде
деп белгілегенде
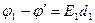
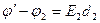
бұл теңдеулерді қосып
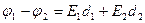 (3.1.6.19)
(3.1.6.19)
потенциалдар айырымын анықтауға болады
 (3.1.6.20)
(3.1.6.20)
Әртүрлі диэлектрик қабаттары бар жазық конденсатордың электр сыйымдылығының формуласын жазамыз
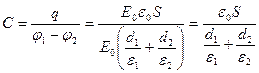 (3.1.6.21)
(3.1.6.21)
5) Конденсаторларды қосу.
Бірнеше конденсаторларды өзара параллель немесе тізбектей жалғастырып батарея құруға болады. Сыйымдылықтары 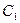 және
және 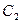 екі конденсатордан құрастырылған батареяның сыйымдылығын есептейік.
екі конденсатордан құрастырылған батареяның сыйымдылығын есептейік.
а) Конденсаторлар өзара тізбектей жалғансын.
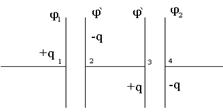
3.6.3 – сурет
1-ші астарының потенциялын  , ал 2 - және 3 - ші астарларының потенциялын
, ал 2 - және 3 - ші астарларының потенциялын  деп, 4 - ші астарының потенциялын
деп, 4 - ші астарының потенциялын  деп белгілейік. 1-ші астарға
деп белгілейік. 1-ші астарға  заряд берсек, 2-ші және 3-ші астарлар электростатикалық индукция заңы бойынша
заряд берсек, 2-ші және 3-ші астарлар электростатикалық индукция заңы бойынша 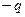 және
және  болып зарядталады (3.1.6.3 – сурет).
болып зарядталады (3.1.6.3 – сурет).
Сонда әрбір конденсатордың астарларындағы потенциалдар айырымы
 (3.1.6.21)
(3.1.6.21) 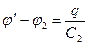 (3.1.6.22)
(3.1.6.22)
бұл формулаларды мүшелей қосып батарея астарларының потенциалдар айырымын табуға болады.
 (3.1.6.23)
(3.1.6.23)
Екінші жағынан  , осы формулаға (3.1.6.23)- ны қойып және (3.1.6.21), (3.1.6.22) формулаларды ескерген жағдайда
, осы формулаға (3.1.6.23)- ны қойып және (3.1.6.21), (3.1.6.22) формулаларды ескерген жағдайда
 (3.1.6.24)
(3.1.6.24)
және
 (3.1.6.25)
(3.1.6.25)
формулаларын аламыз.
Яғни конденсаторлар өзара тізбектей жалғанғанда, осы конденсаторлардағы зарядтар бірдей болып, потенциалдар айырымы қосылады.
б) Конденсаторларды параллель жалғау.
Конденсаторларды өзара параллель жалғағанда потенциалдар айырымы өзгермейді, әр конденсатор астарларының зарядтары әртүрлі болады және төмендегі формулалармен есептеледі.
 (3.1.6.26)
(3.1.6.26)

3.1.6.4 – сурет
осы формулаларды мүшелеп қосқанда
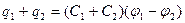 (3.1.6.27)
(3.1.6.27)
Батарея астарларындағы заряд мөлшері екі конденсатордағы зарядтардың қосындысына тең болады
 .
.
Осы өрнекке (3.1.6.28) формуланы қойып
 (3.1.6.28)
(3.1.6.28)
батареяның сыйымдылығының формуласын аламыз.
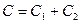 (3.1.6.29)
(3.1.6.29)
3.1.7 Оңашаланған өткізгіштің, зарядтар жүйесінің, зарядталған конденсатордың энергиясы
Заряды 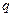 , сыйымдылығы C, потенциалы ц оңашаланған өткізгіш берілсін. Осы өткізгіштің заряды
, сыйымдылығы C, потенциалы ц оңашаланған өткізгіш берілсін. Осы өткізгіштің заряды 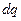 –ге арттырылсын. Сонда істелген жұмыстың шамасы мына формуласымен анықталады.
–ге арттырылсын. Сонда істелген жұмыстың шамасы мына формуласымен анықталады.
 (3.1.7.1)
(3.1.7.1)
Осы формуланы интегралдап, зарядталған өткізгіш энергиясын анықтауға болады.
 (3.1.7.2)
(3.1.7.2)
(3.1.7.1) формуласын төмендегідей түрлендіріп жазуға болады
 (3.1.7.3)
(3.1.7.3)
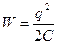 (3.1.7.4)
(3.1.7.4)
Зарядтар жүйесінің энергиясын анықтайық. Зарядталған денелердің өзара әсер күштері консервативті болғандықтан зарядтар жүйесінің потенциалдық энергиясы болады. Арақашықтығы 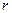 , заряд шамалары
, заряд шамалары 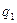 және
және 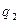 болатын зарядтардың потенциялық энергиялары (3.1.3.7) формула бойынша
болатын зарядтардың потенциялық энергиялары (3.1.3.7) формула бойынша
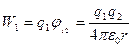 ,
, 
бұдан 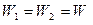 , олай болса
, олай болса

Жалпы  зарядтардан тұратын жүйенің энергиясы
зарядтардан тұратын жүйенің энергиясы
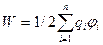
Зарядталған конденсатордың энергиясын есептеу үшін (3.1.7.2) және (3.1.7.3) формулаларындағы ц-ді 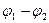 потенциалдар айырымымен алмастырайық
потенциалдар айырымымен алмастырайық
 (3.1.7.5)
(3.1.7.5)
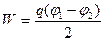 (3.1.7.6)
(3.1.7.6)
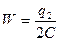 (3.1.7.7)
(3.1.7.7)
мұндағы 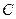 - конденсатордың сыйымдылығы.
- конденсатордың сыйымдылығы.
Осы формулаларды пайдаланып, конденсатор астарларының бір-біріне тартылу күшін анықтайық.
Ол үшінконденсатор астарларының арақашықтықтарын 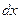 қашықтыққа өзгертейік, сол кезде жұмыс
қашықтыққа өзгертейік, сол кезде жұмыс  потенциялық энергияның кемуі есебінен істеледі. Бұдан
потенциялық энергияның кемуі есебінен істеледі. Бұдан
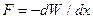 (3.1.7.8)
(3.1.7.8)
(3.1.7.7) мен (3.1.6.9) формулалары бойынша
 (3.1.7.9)
(3.1.7.9)
немесе
 (3.1.7.10)
(3.1.7.10)
Минус (-) таңбасы күштің тартылыс күші екендігін көрсетеді.
Электростатикалық өрістің энергиясын анықтау үшін (3.1.7.5) формуланы түрлендіріп жазайық. 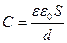 және
және  формулаларын ескере отырып
формулаларын ескере отырып
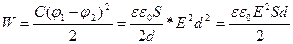 (3.1.7.11)
(3.1.7.11)
деп жазуға болады, мұндағы  конденсатордың көлемі.
конденсатордың көлемі.
Жазық конденсатордың өріс энергиясының тығыздығы анықтауға болады.
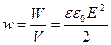 (3.1.7.12)
(3.1.7.12)
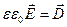 формуласын ескергенде
формуласын ескергенде
 (3.1.7.13)
(3.1.7.13)
тең болады.
 формуласын пайдаланып өрістің энергия тығыздығын төмендегідей жазуға болады:
формуласын пайдаланып өрістің энергия тығыздығын төмендегідей жазуға болады:
 (3.1.7.14)
(3.1.7.14)
мұндағы  -
- 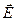 өрісінің бостықтағы энергия тығыздығы,
өрісінің бостықтағы энергия тығыздығы,  - диэлектрикті поляризациялауға жұмсалатын энергия тығыздығы болып табылады. Осыны дәлелдейік. Диэлектрик поляризациясы дегеніміз зарядтардың сыртқы өрісі салдарынан ығысуы. Сол кезде оның бір өлшем көлеміндегі жұмыстың мөлшері
- диэлектрикті поляризациялауға жұмсалатын энергия тығыздығы болып табылады. Осыны дәлелдейік. Диэлектрик поляризациясы дегеніміз зарядтардың сыртқы өрісі салдарынан ығысуы. Сол кезде оның бір өлшем көлеміндегі жұмыстың мөлшері
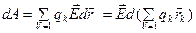
мұндағы  – бір өлшем көлемдегі диполь моменті. Соңғы формуланы мына түрде жаз
– бір өлшем көлемдегі диполь моменті. Соңғы формуланы мына түрде жаз
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 6392; Нарушение авторских прав?; Мы поможем в написании вашей работы!