Лоренц формуласы

Магнит өрісіндегі бойында тоғы бар өткізгіштің 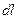элементіне әсер ететін күш Ампер заңы бойынша

(3.3.5.1)

болады. Ал, электр тоғы зарядталған бөлшектердің бағатталған қозғалысы болғандықтан магнит өрісі зарядқа әсер ететін болады. Осы күшті есептейік. Егер көлем бірлігіндегі заряд саны n₀, зарядтардың қозғалыс жылдамдығы 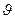, өткізгіштің көлденең қимасының ауданы Ң болсын, сонда бір өлшем уақыт ішінде өткізгіштің көлденең қимасы арқылы өтетін заряд саны 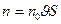, ал тоқтың шамасы , мұнда q – бір зарядтың шамасы. Яғни, тоқ

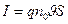
Бұл өрнекті шаманы (3.3.5.1) формуласына қойып

(3.3.5.2)

өткізгіштің 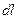бөлігене әсер ететін Ампер күшін табамыз. Осы бөліктегі заряд саны болады. Ендеше, бір зарядқа әсер етуші күш

(3.3.5.3) болады

Бұл өрнекті векторлық түрде жазатын болсақ

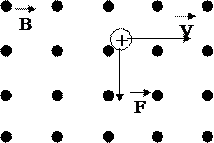
3.3.5.1 – сурет

(3.3.5.3) теңдігі Лоренц формуласы делінеді. Ескерте кететін жағдай, магнит өрісі тек қозғалушы зарядқа әсер етеді, тыныштықтағы зарядқа әсер етпейді. Лоренц күшінің бағыты сол қол ережесі арқылы анықталады. Егер сол қолымыздың алақанына векторы кіретіндей, ал жазылған төрт саусақ оң зарядтардың қозғалыс бағытын көрсететіндей етіп ұстасақ, 90⁰ – қа қайырған бас бармақ Лоренц күшінің бағытын көрсетеді (3.3.5.1 – сурет). Суреттегі векторының бағыты сурет жазықтығынан бізге қарай бағытталған. Егер магнит өрісіндегі заряд теріс болса, Лоренц күші жоғары бағытталады (3.3.5.2 – сурет).

3.3.5.2 – сурет

Лоренц күші әр уақытта зарядталған бөлшектің қозғалыс жылдамдығына перпендикуляр болады. Сондықтан, бұл күш зарядталған бөлшектің шамасына әсерін тигізбейді, тек бағытын өзгертеді. Ендеше, Лоренц күші жұмыс істемейді. Шынында . Егер қозғалушы зарядқа магнит өрісімен қатар электр өрісі де әсер етсе, онда қорытқы күш

(3.3.5.4)

өрнегіне тең болады.

3.3.6 Магнит өрісінде зарядталған бөлшектердің қозғалысы

Зарядының шамасы q бөлшек біртекті магнит өрісіне векторына перпендикуляр бағытта ұшып кіреді делік (3.3.6.1 – сурет).

3.3.6.1 – сурет

Сонда зарядқа әсер етуші Лоренц күші модулі жағынан тұрақты, ал бағыты бөлшектің траекториясына перпендикуляр болғандықтан, ол күш центрге тартқыш күш болып табылады.

(3.3.6.1)

бұдан бөлшектің шеңбер бойымен қозғалысының 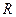радиусын анықтауға болады:

(3.3.6.2)

Бөлшектің осы шеңберді толық бір айналыс жасауға кететін уақытын айналыс периоды деп атайды:

(3.3.6.3)

Айналыс периоды бөлшектің жылдамдығына байланыссыз, индукция векторы мен зарядтың шамасына кері пропорционал болады.

Енді 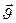жылдамдықпен индукция векторына a бұрышын жасай ұшып кірген зарядталған бөлшектің қозғалу сипатын қарастырайық (3.3.6.2 – сурет).

3.3.6.2-сурет

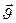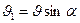векторын -ға перпендикуляр және параллель екі құраушысына жіктейік. Сонда Лоренц күші

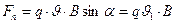
және бұл векторына перпендикуляр жазықтықта жатады. Жылдамдықтың векторына параллель құраушысынан 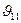туатын F_л =0, өйткені 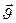және арасындағы бұрыш нөлге тең, магнит өрісі бөлшекке әсер етпейді, сондықтан ол түзу сызықты және бірқалыпты қозғалады. Зарядталған бөлшектің қозғалысы екі қозғалыстың қосылуынан туады:

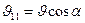1) векторының бойымен жылдамдықпен шеңбер бойымен түзу сызықты қозғалыс.

2) векторына перпендикуляр жазықтықта жылдамдықпен шеңбер бойымен бір қалыпты айналыс.

Осы екі қозғалыстың қосылуы нәтижесінде бөлшек спираль бойымен қозғалады. Спиральдің өсі векторына паралелль болады. Шеңбердің радиусы (3.3.6.2) формуласымен анықталады. Винттің сызықтық адымы

немесе (3.3.6.3) формуласын ескеретін болсақ

(3.3.6.4)

болады.

Спираль бұралатын бағыт бөлшек зарядының таңбасына байланысты болады. Біздің қарастырып отырғанымыз теріс зарядтардың магнит өрісіндегі қозғалысы. Егер оң заряд болса, онда спираль сағат тіліне қарсы бұралады.

Дата добавления: 2014-10-15