Парамагнетизм

Сыртқы өріс жоқ кездің өзінде 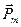магниттік моменті нөлден өзгеше болатын заттарды парамагнетиктер деп атайды. Бірақ жылулық қозғалыстың әсерінен олардың магниттік моменттері ретсіз орналасады. Сондықтан парамагнетиктердің магниттік қасиеттері болмайды.

Егер парамагнитиктерді магнит өрісіне әкелсе, онда оның атомының магниттік моментері өріс бойынша бағдарланады. Сонымен парамагнетик магниттеліп сыртқы магнит өрісімен бағыттас болатын өзінің меншікті өрісін тудырады. Бұл парамагниттік эффект делінеді. Сыртқы өрісті нөлге дейін азайтса, онда жылулық қозғалыс салдарынан магниттік моменттердің реттілігі бұзылады да, парамагнетик магнитсізденеді. Парамагнетиктерге Жерде сирек кездесетін элементтер жатады.

3.3.20. Магниттелу. Заттардағы магнит өрісі

Магнетиктердің магниттелуін сандық тұрғыдан сипаттау үшін векторлық шама - магниттелу векторы - енгізіледі:

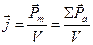(3.3.20.1)

- магнетиктердің магниттік моменті жеке молекулалардың магниттік моменттерінің қосындысына тең болады.

Егер сыртқы магнит өрісі 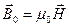, ал магниттелген зат өрісін тудыратын болса, онда қорытқы өріс

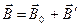(3.3.20.2)

болады.

Молекулалық тоқтардың тудыратын магниттік өрісін түсіну үшін, ұзындығы 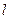, көлденең қимасы S цилиндр түрдегі магнетикті алайық (3.3.19.2 – сурет). Оны біртекті магнит өрісіне қойғанда, магнетик магниттеледі, яғни молекулалық тоқтар бағдарланады. Егер цилиндрдің қимасын қарастырсақ, онда магнетиктің ішкі бөлігінде молекулалық тоқтар сыртқы өріске қарама – қарсы бағытталады да өзара компенсацияланады. Цилиндрдің бүйір беті арқылы жүрген тоқ соленоидтағы тоққа пара-пар болады. Соленоид бір орамнан тұрады деп) оның магнит өрісінің индукциясы үшін

(3.3.20.3)

деп жазамыз, мұндағы 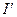- молекулалық тоқ күші: 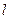- цилиндрдің ұзындығы.

3.3.20.2 – сурет

Осы тоқтың магниттік моменті

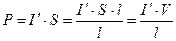
мұндағы - магнетик көлемі және екендігін ескерген жағдайда, магнетиктің магниттелуі

болады, ендеше (3.3.20.3) формуласын

(3.3.20.4)

деп жазуға болады..

және екенін ескеріп (3.3.19.2) формуласын мына түрде жазамыз:

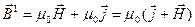(3.3.20.5)

Тәжірибелер әлсіз өрістерде магниттелу векторы магнит өрісінің кернеулігіне тура пропорционал болатындығын көрсетті:

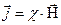(3.3.20.6)

мұндағы 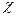– магниттік қабылдағыштық немесе магниттелу коэффициенті делінеді.

Диамагнетиктер үшін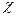теріс (молекулалық тоқтар өрісі сыртқы өріске қарсы болады), парамагентиктер үшін 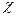оң (молекулалық тоқтар өрісі мен сыртқы өріс бағыттас) болады. (3.3.19.5) –ға (3.3.19.6)– ны қойсақ

(3.3.20.7)

шығады.

- заттардың магниттік өтімділігі делінеді, онда

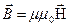(3.3.20.8)

болып шығады.

Сонымен диэлектриктер үшін және , парамагнетиктер үшін және.

векторының циркуляциясы теоремасы бойынша

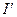мұндағы - өткізгіштік тоқ, - молекулалық тоқ.

Сонымен, кез келген тұйық контурдағы магнит индукциясының циркуляция векторы осы контур қамтитын молекулалық тоқтар мен өткізгіштік тоқтардың алгебралық қосындысына тең болады.

Магниттелу циркуляциясы

(3.3.20.9)

болады (осы контурды қамтитын молекулалық тоқтардың қосындысына тең).

Заттардағы магнит өрісі үшін толық тоқ заңы

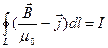(3.3.20.10)

немесе

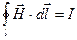(3.3.20.11)

болады, мұндағы .

Дата добавления: 2014-10-15