Ферромагнетиктер

Магниттік өтімділігі өте жоғары заттарды ферромагнетиктер деп атайды. Ферромагнетиктерге темір, никель, кобальт және кейбір қорытпалар жатады.

Ферромагнетиктердің негізгі ерекшеліктері мынадай болады:

1)ферромагнетиктердің магниттелуі сыртқы магниттеуші өріс жойылғаннан кейін де сақталады;

2)магниттік өтімділік 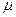мен магниттік қабылдағыштық 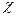тұрақты болмайды, олар магниттеуші өріске байланысты болады.

Ферромагнетиктерде магниттелу алғашқыда сыртқы - тың артуына байланысты тез артады, содан кейін баяулайды, соңында -қа байланысты болмайтын -магниттік қанығу мәніне жетеді (3.3.21.1- сурет).

Бұндай байланыстылықтың себебі: магниттеуші өріс артқанда молекулалық магниттік моменттердің өріс бойынша реттелу дәрежесі артады, бірақ моменттері реттелмеген молекулалар азайғанда бұл процесс баяулайды. Соңында барлық моменттер реттелгеннен кейін – дің артуы тоқталады, магниттік қанығу басталады, 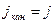болады.

Ферромагниттердің негізгі қасиеттерінің бірі 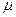-дің үлкен болуында (супермаллойда ) ғана емес, сонымен қатар 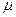-дің -қа байланыстылығында. Алғашқыда артқанда 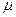– де артады, қандай да бір максимум шамаға жетіп қайтадан кеми бастайды да, соңында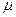 1 ұмтылады. (3.3.21.2- сурет).

(3.3.20.8)-ден 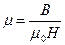, (3.3.20.7)-ден , (3.3.20.6)-ден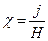

ендеше

3.3.21.1 – сурет 3.3.21.2 – сурет

болады. Сондықтан 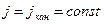болғанда Н артуына байланысты , ал 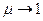ұмтылады.

Магниттік гистерезис құбылысын қарастырайық. Айталық ферромагнитті қанығуға дейін магниттеп, бұдан соң магниттеуші кернеуді азайта бастағанда j-дің кемуі 1-2 қисықпен анықталады (0-1 қисығынан жоғары орналасады). H=0 болғанда j нөлге тең болмайды, яғни ферромагнетикте 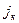қалдық магниттелу болады. Қалдық магниттелуді жою үшін өріс бағытын өзгерту керек. Кернеулігі H_c осы қарсы өрістің әсерінен_. j=0 болады. сондықтан кернеулік H_c коэрцитивтік күш делінеді. Теріс кернеулікті әрі қарай арттыра отырып (3-4 қисығы) ферромагнитті кері магниттеуге болады. Кернеуліктің мәнінде тағы 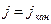болады. Бұдан кейін ферромагнетикті тағы да магнитсіздендіріп (4-5-6 қисығы), одан кейін қайта қанығуға дейін магниттейді (6-1 қисығы).

Сонымен айнымалы магнит өрісі арқылы ферромагнетиктің магниттелуін 1-2-3-4-5-6-1 қисығы бойынша өзгертуге болады. Мұны гистерезис тұзағы деп атайды. Гитерезис ферромагнетиктің магниттелуі ферромагниттің магниттелуінің H - нің бір мәнді функциясы бола алмайтындығын көрсетеді, яғни H- тің бір мәніне -дің бірнеше мәні сәйкес келеді.

Егер Н-тың максимал мәнінде магниттік қанығуы болса, онда тұзақты гистерезистің максимал тұзағы деп атайды (3.3.21.3 -суреттегі тұтас сызық). Егер амплитудалық мәнінде қанығуға жетпесе, онда жеке цикл деп аталатын тұзақ шығады (3.3.21.3 -суреттегі үзік сызықтармен көрсетілген тұзақ).

Әртүрлі ферромагнетиктер әртүрлі гистерезис тұзағын береді.Коэрцитивтік күші аз болатын ферромагниттер жұмсақ ферромагнетиктер делінеді (жіңішке тұзақты гистерезис), коэрцитивтік күші

үлкен болатын ферромагнетиктер қатқыл ферромагнетиктер деп аталады. Бұлардың тұзағы кеңдеу болады. Осындай қасиеттеріне сәйкес ферромагнетиктердің қолданылатын орындары түрліше болады. Мысалы, қатқыл ферромагнетиктер тұрақты магнит жасауға, ал жұмсақ ферромагнетиктер трансформатор өзегін жасауға қолданылады.

j_қан

3.3.21.3 -сурет

Ферромагнетиктердің магниттік қасиеті температураға да байланысты болады. Кюри нүктесі деп аталатын температурада ферромагнетиктердің магниттік қасиеті жойылады. Ферромагнетиктердің температурасын Кюри нүктесінен жоғары көтерсе, ферромагнетик кәдімгі парамагнетике айналады. Заттар Кюри нүктесінде ферромагнетик күйден парамагнетик күйге жылу шығарусыз немесе жұтусыз өтеді. Мұндай ауысу екінші ретті фазалық ауысу делінеді. Яғни, Кюри нүктесінде екінші ретті фазалық ауысу өтеді.

Ферромагнетиктер магниттелгенде деформацияланады, яғни ұзындық мөлшері, көлемі өзгереді. Мұндай құбылысты магнитострикция деп атайды. Магнитострикциялық эффектің шамасы және бағыты ферромагнетиктердің табиғатына, магнит өрісінің бағытына қатысты кристалографиялық өстің бағдарына және өрістің кернеулігіне байланысты болады.

3.3.22 Ферромагнетизмнің табиғаты

Ферромагнетизм теориясын Вейсс жасады. Бұл теорияны кванттық механика тұрғысынан әрі қарай дамытқан Я.Н.Френкель және В.Гейзенберг болды.

Вейсс бойынша, ферромагнетиктер Кюри нүктесінен төменгі температурада өздігінен (өріс жоқ кезде де) магниттеледі. Оның себебі ферромагнетиктерде өздігінен магниттелген кішкене аймақтар - домендер болады. Сыртқы өріс болмаған кезде жеке домендердің магниттік моменттері ретсіз орналасады да бірін – бірі компенсациялайды, ферромагнетиктің қорытқы магниттік моменті нөлге тең болады. Сондықтан магнит өрісімен әсер еткенде өріс жаңағы тұтас аймақтардың магниттік моменттерін бағдарлайды, Н артқанда 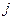магниттелу мен магнит индукциясы да артады. Бұл ферромагнетиктердің магниттік өтімділігі 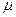әлсіз өрістерде кенет артып максимумға жететіндігін көрсетеді. (3.3.22.1 – сурет).

3.3.22.1 – сурет

Эксперименттер В магнит индукциясының сыртқы өрістің Н кернеулігіне байланыстылығы секірмелі түрде болатындығын көрсетеді. (3.3.22.2 - сурет). Бұл жағдай ферромагнетик ішіндегі домендердің өріс бойынша секірмелі бұрылатындығын көрсетеді. Сыртқы магнит өрісі нөлге дейін кемігенде домендердің магниттік моменттерін ретсіздендіруге шамасы келмейтіндігіне көз жеткізеді..

Сондықтан магниттік гистерезис құбылысы болады. Ферромагнетикті магнитсіздендіру кезінде коэрцитивтік күш қажет.

3.3.22.2 – сурет

Кюри нүктесінен жоғары температурада домендік структура бұзылады. Сондықтан Кюри нүктесінен жоғары температурада ферромагнетик парамагнетикке айналады.

Ферромагнетиктерде домендердің болуы тәжірибелермен дәлелденген. Домендердің сызықтық мөлшері 10^-4 10^-2 см.

Қазіргі уақытта ферромагнетиктердің магниттік қасиеттері электрондардың спиндік магниттік моменттері арқылы анықталатындығы тағайындалды. Ферромагниттік қасиеттер тек кристаллды заттарда ғана болатындығы анықталды. Өйткені олардың атомдарында спиндері компенсацияланбаған электрондық қабықшалар болады. Мұндай кристалдарда электрондардың спиндік магниттік моменттерін бір-біріне параллель етіп орналастырушы күштер пайда болуы мүмкін. Осы күштер спонтандық магниттелу аймақтарын тудырады. Бұларды ауыстырғыш күштер деп атайды. Монокристалдарда магниттік қасиеттердің анизотроптығы байқалады. Тәжірибелер кристалдардың бағыт бойынша магниттелу қасиетін анықтады: кернеуліктің бір мәнінде бір бағытта магниттелу өте үлкен болса (жеңіл магниттелу бағыты), екінші бағыттарында аз болады (қиын магниттелу бағыты).

Кейбір жағдайларда ауыстырғыш күштер электрондардың спиндік магниттік моменттерін антипараллель етіп бағдарлайды. Мұндай денелер антиферромагнетиктер делінеді. Антиферромагнетиктерге марганец қопалары (MnO, MnF₂), темір қоспалары (FeO, FeCl₂ …) жатады. Бұларда да антиферромагниттік Кюри нүктесі (Неел нүктесі) болады, бұл кезде спиндердің антипараллель бағдары жоғалады да парамагнетикке айналады.

Соңғы уақыттарда жартылай өткізгіштік ферромагниттер – ферриттер радиотехникада, есептегіш техникада пайдаланылып жүр. Олар металдардан өзінің ферромагнетиктік қасиеттерімен және үлкен электрлік кедергілерімен ерекшеленеді.

3.3.23 Электромагниттік өріс. Құйынды электр өрісі

Максвелл бойынша, кез келген айнымалы магнит өрісі өз айналасында индукциялық тоқты тудыруы электр өрісінің пайда болуына әкеледі. Осы электр өрісінің циркуляциясы

(3.3.23.1)

болады. екендігін ескеріп

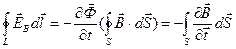(3.3.23.2)

деп жазуға болады.

Сонымен өткізгіште тоқ тудыратын (зарядтарды қозғалысқа келтіретін) электр өрісі. Ал бұл өрісіті тудыратын айнымалы магнит өрісі. Магнит өрісі өзгергенде пайда болатын электр өрісі электростатикалық өрістен мүлде өзгеше. Электростатистикалық өрісте кернеулік сызықтары зарядтардан басталып зарядтардан аяқталады. Магнит өрісінің өзгеруінен туатын электр өрісі магнит өрісі сияқты құйынды болады.

Құйынды электр өрісінің магнит өрісі сияқты оң зарядты орын ауыстыру жұмысы қозғалмайтын өткізгіштегі индукция э.қ.к – і болып табылады.

3.3.24 Ығысу тоғы

Максвелл бойынша, кез келген айнымалы магнит өрісі өзінің айналасындағы кеңістікте құйынды электр өрісін тудырады. Ендеше кері құбылыс: электр өрісінің кез келген өзгерісі өзін қоршаған кеңістікте құйынды магнит өрісін тудыруы керек. Магнит өрісін тудырушы айнымалы электр өрісін Максвелл ығысуы деп атады.

Конденсаторы бар айнымалы электр тоғының тізбегін қарастырайық (3.3.24.1-сурет). Конденсатор астарлары арасында айнымалы электр өрісі болады, ендеше астарлар арқылы ығысу тоғы жүру керек. Тізбек тұйық болғанда конденсаторды қосатын өткізгіш арқылы жүретін өткізгіштік тоқ

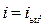(3.3.24.1)

Өткізгіштік тоқ тығыздығы:

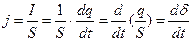(3.3.24.2)

мұнда - беттік заряд тығыздығы, S-конденсатордың астарларының ауданы.

Ендеше ығысу тоғының тығыздығы

(3.3.24.3)

Конденсатордағы электрлік ығысу болғандықтан

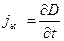(3.3.24.4)

болады. Меншікті туынды белгісі магнит өрісі тек уақыт бойынша тез өзгеретін электрлік ығысу арқылы анықталатындығын көрсетеді.

3.3.24.1 – сурет

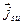жәневекторларының бағытын анықтайық.

Конденсатордың зарядталуы кезінде оның астарларын қосатын өткізгіш арқылы жүретін тоқ оң астардан сол жақ астарға қарай бағытталады (3.3.24.2 – сурет). Бұл уақытта конденсатордағы өріс күшейеді де 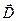векторы артады .

3.3.24.2 – сурет 3.3.24.3 – сурет

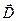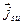Яғни – векторы мен векторы бағыттас болады, ендеше және векторларының да бағыттас екендігі көрінеді. Конденсатордың разрядталуы кезінде (3.3.24.– сурет) астарларды қосатын өткізгіш арқылы жүретін тоқ сол жақ астардан оң жақ астарға қарай бағытталады. Конденсатордағы өріс нашарлайды да, 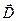векторы кемиді,, яғни векторы 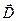векторына қарсы бағытталған. Бірақ векторы векторымен бағыттас, ол 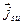векторымен бағыттас. Осы айтылғандардан (3.3.24.2) формуланы векторлық түрде мына түрде жазуға болады:

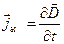(3.3.24.5)

Сонымен электр өрісінің кез келген өзгерісі ығысу тоғын және онымен байланысты магнит өрісін тудырады. Магнит өрісінің индукция сызықтары (3.3.24.2) және (3.3.24.3)– суреттерде үзік сызықтармен көрсетілген. Өткізгіштік тоқ пен ығысу тоғы тек магнит өрісін тудыру жағынан ғана бір – біріне эквивалентті, ал басқа қасиеттері өзгеше. Мысалы, ығысу тоғы Джоуль -Ленц жылуын шығармайды.

Электрлік индукция векторы екі қосындыдан тұрады, мұндағы 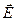– электростатистикалық өріс кернеулігі, - поляризация векторы, ендеше ығысу тоғы

(3.3.24.6.)

болады, мұндағы – вакуумдағы ығысу тоғының тығыздығы, - поляризация тоғының тығыздығы. Поляризация тоғы табиғаты жағынан өткізгіштік тоқ сияқты, сондықтан оның магнит өрісін тудыруы табиғи нәрсе. Ал ығысу тоғы электр өрісінің уақытқа байланысты өзгеруі, бұл да магнит өрісін тудырады.

Максвелл бойынша толық тоқ тығыздығы

(3.3.24.7)

деп жазылады және (3.3.23.1) формула бойынша

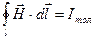
болады. Ал 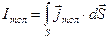, ендеше

(3.3.24.8)

болып, векторының циркуляциясының жалпыланған теоремасы шығады.

(3.3.24.8) теңдігі әрқашан да дұрыс, себебі тәжірибе нәтижелері теориямен сәйкес келеді.

3.3.25 Электромагниттік өріс үшін Максвелл теңдеулері

Электромагниттік өріс туралы Максвелл теориясының негізіне өзіміз қарастырған мына теңдеулер жатады:

1) 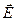векторының циркуляциясы:

(3.3.25.1)

Бұл теңдеу электр өрісін тек электр зарядтары ғана емес, өзгермелі магнит өрісі де тудыратындығын көрсетеді.

2) векторының циркуляциясының жалпыланған теоремасы:

(3.3.25.2)

Бұл теңдеу магнит өрісін қозғалушы электр зарядтары не өзгермелі электр өрісі тудыратынын көрсетеді.

3) 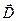векторы үшін Гаусс теоремасы:

(3.3.25.3)

мұндағы 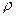– зарядтардың көлемдік тығыздығы.

4) өрісі үшін Гаусс теоремасы:

(3.3.25.4)

Сонымен Максвелл теңдеулерінің толық жүйесі интегралдық түрде былай жазылады:

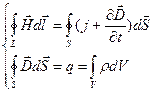
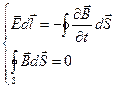
Стационарлық өріс үшін (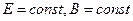) Максвелл теңдеулері мынадай:

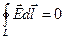
Векторлық анализдегі Стокс теоремасы бойынша

(3.3.25.5)

Дата добавления: 2014-10-15