
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Холл эффектісі
|
|
|
|
Егер бойында тоғы бар пластинаны магнит өрісіне перпендикуляр етіп орналастырсақ, онда тоқ пен өріске ( ) параллель болатын жақтары (А және С) арасында потенциалдар айырмасы (цА – цС) пайда болады (3.3.8.1-сурет). Бұл құбылыс Холл эффектісі делінеді.
) параллель болатын жақтары (А және С) арасында потенциалдар айырмасы (цА – цС) пайда болады (3.3.8.1-сурет). Бұл құбылыс Холл эффектісі делінеді.
Пайда болған потенциалдар айырмасы (цА– цС) тоқ пен магнит өрісінің индукциясының көбейтіндісіне тура пропорционал және пластина қалыңдығына кері пропорционал болады
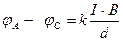 (3.3.8.1)
(3.3.8.1)
мұндағы 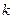 - әртүрлі металдар үшін өзгеше болатын пропорционалдық коэффицент немесе Холл тұрақтысы делінеді.
- әртүрлі металдар үшін өзгеше болатын пропорционалдық коэффицент немесе Холл тұрақтысы делінеді.
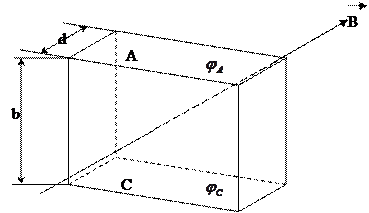
3.3.8.1-сурет
Холл эффектісі электрондық теория бойынша оңай түсіндіріледі. Электр тоғының өзі зарядталған бөлшектердің қозғалысы болғандықтан, магнит өрісіндегі қозғалушы зарядқа Лоренц күші әсер етеді:
 (3.3.8.2)
(3.3.8.2)
Бұл күштің әсерінен электрондар пластинаның жоғарғы жағына (А) жинала бастайды да А және С арасында (цА – цС) потенциалдар айырмасы пайда болады. Осы потенциалдар айырмасының тудыраған электр өрісінің кернеулігі
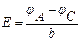
болады, ендеше электронға әсер етуші электрлік күш
 Стационарлық күйде
Стационарлық күйде 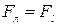 болады, яғни
болады, яғни 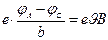
бұдан
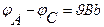 (3.3.8.3)
(3.3.8.3)
болады. Тоқ күші 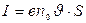 , ал пластинаның ауданы
, ал пластинаның ауданы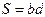 болғандықтан
болғандықтан
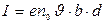
бұл формуладан
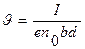 (3.3.8.4)
(3.3.8.4)
(3.3.8.4)-ны (3.3.8.3)-ға қойып
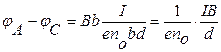 (3.3.8.5)
(3.3.8.5)
деп жазамыз. (3.3.8.1) экспериментальдық формуламен салыстырып Холл тұрақтысын анықтауға болады:
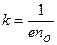
3.3.9. Магнит өрісіндегі тоғы бар тұйық контур
Егер тоғы бар тұйық контурды біртекті магнит өрісіне орналастырса, онда оның  элементіне әсер ететін Ампер күші
элементіне әсер ететін Ампер күші

арқылы анықталады (3.3.9.1 – сурет).
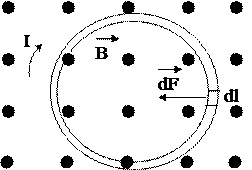
3.3.9.1 – сурет
Күштің бағыты сол қол ережесі арқылы анықталады. (3.3.9.1) – суреттегі 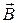 векторы сурет жазықтығына перпендикуляр және суреттен сізге қарай бағытталған, ал контурдағы тоқ сағат тіліне бағыттас. Сонда контурдың
векторы сурет жазықтығына перпендикуляр және суреттен сізге қарай бағытталған, ал контурдағы тоқ сағат тіліне бағыттас. Сонда контурдың  элементіне әсер етуші күші
элементіне әсер етуші күші 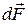 контурдың центріне қарай бағытталады. Егер өріс біртекті болса, контурға сығушы күш әсер етеді. Ал тоқтың бағытын немесе индукция векторының бағытын өзгертсе, онда контурға керуші күш әсер етеді.
контурдың центріне қарай бағытталады. Егер өріс біртекті болса, контурға сығушы күш әсер етеді. Ал тоқтың бағытын немесе индукция векторының бағытын өзгертсе, онда контурға керуші күш әсер етеді.
Енді бойында тоғы бар тұйық контур жазықтығына 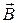 векторы параллель болсын дейік (3.3.9.2 - сурет).
векторы параллель болсын дейік (3.3.9.2 - сурет).

3.3.9.2 – сурет
Kонтурдың  және
және 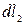 элементтеріне
элементтеріне 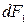 және
және  күштер әсер етеді. Суретте сол қол ережесі бойынша
күштер әсер етеді. Суретте сол қол ережесі бойынша  элементіне әсер етуші күш
элементіне әсер етуші күш 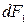
 элементіне перпендикуляр және суреттен бізге қарай бағытталады, ал
элементіне перпендикуляр және суреттен бізге қарай бағытталады, ал 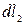 элементіне әсер етуші
элементіне әсер етуші  күші
күші 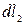 -ге перпендикуляр және бізден суретке қарай бағытталады деп есептейміз.
-ге перпендикуляр және бізден суретке қарай бағытталады деп есептейміз. 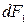 күшінің шамасы
күшінің шамасы 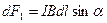 және
және 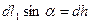 болғандықтан
болғандықтан

Дәл осылай 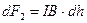 болатындығына да көз жеткізуге болады. Яғни, dF1= dF2. Осыдан
болатындығына да көз жеткізуге болады. Яғни, dF1= dF2. Осыдан  және
және 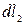 элементтеріне қос күш әсер ететіндігін көруге болады. (dF1 және dF2 күштерінің бағыттары қарама-қарсы және өзара параллель). Қос күш моменті
элементтеріне қос күш әсер ететіндігін көруге болады. (dF1 және dF2 күштерінің бағыттары қарама-қарсы және өзара параллель). Қос күш моменті

ал 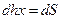 (3.3.9.2–суреттегі штрихталған бөліктің ауданы). Ендеше
(3.3.9.2–суреттегі штрихталған бөліктің ауданы). Ендеше
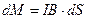
болады.
Контурдағы осындай барлық параллель тілікшелердің күш моменттерін қосып
 (3.3.9.1)
(3.3.9.1)
контурға әсер ететін қорытқы күшті табамыз, мұндағы Pm= IS контурдың магниттік моменті.
Енді контур жазықтығы мен магнит өрісі кез келген бұрыш жасасын делік (3.3.9.3– сурет). 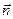 нормаль мен магнит өрісінің бағыты арасындағы бұрыш
нормаль мен магнит өрісінің бағыты арасындағы бұрыш 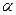 болсын.
болсын.  векторын екі құраушыға жіктейік (
векторын екі құраушыға жіктейік ( -контур жазықтығына перпендикуляр және
-контур жазықтығына перпендикуляр және 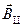 - контур жазықтығына параллель құраушылар).
- контур жазықтығына параллель құраушылар).

3.3.9.3 - сурет
Сурет бойынша бұл құраушылар 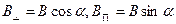 болады.
болады.  құраушысы контурды сығатын немесе керетін күшті тудырады, ал
құраушысы контурды сығатын немесе керетін күшті тудырады, ал 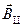 құраушысы айналдырушы моментті тудырады.
құраушысы айналдырушы моментті тудырады.
 (3.3.9.2)
(3.3.9.2)
векторлық түрде
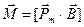
жазылады.
Eнді тоғы бар тұйық контур әр текті магнит өрісінде орналассын дейік.  векторы радиальды сызықтар болады (3.3.9.4- сурет). Зерттеуді оңайлату үшін контурды шеңбер деп алайық. Контур центріндегі
векторы радиальды сызықтар болады (3.3.9.4- сурет). Зерттеуді оңайлату үшін контурды шеңбер деп алайық. Контур центріндегі 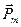 векторы және
векторы және векторы бағыттас болсын. А нүктесіндегі контурдың dl элементіне әсер етуші dF1 күшті анықтайық.
векторы бағыттас болсын. А нүктесіндегі контурдың dl элементіне әсер етуші dF1 күшті анықтайық.
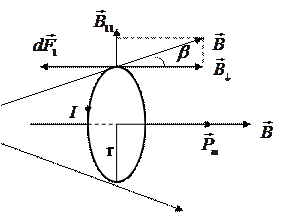
3.3.9.4- сурет
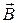 векторын екі құраушыға
векторын екі құраушыға 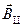 және
және  – ге жіктейік. (
– ге жіктейік. (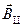 векторы рама жазықтығына параллель, ал
векторы рама жазықтығына параллель, ал  векторы рама жазықтығына перпендикуляр).
векторы рама жазықтығына перпендикуляр).  құраушысы контур керуші күшті тудырады.
құраушысы контур керуші күшті тудырады. 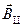 құраушысы dF1 күшін тудырады. Бұл күштің бағыты сол қол ережесі бойынша анықталады да контур жазықтығына перпендикуляр болады. Күш шамасы
құраушысы dF1 күшін тудырады. Бұл күштің бағыты сол қол ережесі бойынша анықталады да контур жазықтығына перпендикуляр болады. Күш шамасы  -ге тең. Минус таңбасы күштің сол жаққа қарай бағытталғандығын көрсетеді.
-ге тең. Минус таңбасы күштің сол жаққа қарай бағытталғандығын көрсетеді. 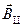 құраушысы
құраушысы  ендеше dF1 күші
ендеше dF1 күші  болады (бұрыш
болады (бұрыш 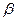 аз болғанда
аз болғанда 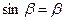 ). Тұтас контурға әсер етуші күш
). Тұтас контурға әсер етуші күш
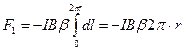 (3.3.9.3)
(3.3.9.3)
Сонымен біртекті магнит өрісіндегі контурға оны қозғауға ұмтылатын күш әсер етеді.
(3.3.9.3) формуладағы  -ға тең дегенде
-ға тең дегенде
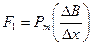 (3.3.9.4)
(3.3.9.4)
болады. Мұндағы  магнит өрісінің градиенті (өрістің әртектілігін сипаттайтын шама).
магнит өрісінің градиенті (өрістің әртектілігін сипаттайтын шама).  – контурдың магниттік моменті. Біртекті өрісте
– контурдың магниттік моменті. Біртекті өрісте  =0 тең болады, сондықтан қозғайтын күш болмайды.
=0 тең болады, сондықтан қозғайтын күш болмайды. 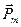 мен
мен  бағыттас болғанда F1 күші өрістің күшті жағына қарай бағытталады, ал бағыттары қарама – қарсы болғанда F1 күші өрістің әлсіз жағына қарай бағытталады, бірақ бұл жағдай орнықсыз болады.
бағыттас болғанда F1 күші өрістің күшті жағына қарай бағытталады, ал бағыттары қарама – қарсы болғанда F1 күші өрістің әлсіз жағына қарай бағытталады, бірақ бұл жағдай орнықсыз болады.
Сонымен бойында тоғы бар контур әртекті магнит өрісінде болғанда F қозғаушы күш және М айналдыру момент әсер етеді.
3.3.10 Магнит өрісіндегі өткізгіш және тоғы бар тұйық контур орын ауыстырғанда істелетін жұмыс
Кез келген бет арқылы өтетін магнит индукциясы векторының ағыны
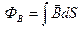 (3.3.10.1)
(3.3.10.1)
формуласына тең. Бір текті өріс үшін

Магнит индукциясының ХБ жүйесіндегі бірлігі [В] =Тл.(Тесла), магнит ағынының бірлігі [Ф]=[B][S]=1Тл1м2=1Вб. (Вебер).
Мысал ретінде, соленоид арқылы өтетін  векторының ағынын есептейік. Соленоид ішіндегі біртекті магнит өрісінің индукциясы
векторының ағынын есептейік. Соленоид ішіндегі біртекті магнит өрісінің индукциясы
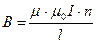
формуласымен анықталады.
Соленоидтың бір орамы арқылы өтетін магнит ағыны Ф1=BS болады. Aл тұтас соленоид арқылы өтетін магнит ағыны
 (3.3.10.2)
(3.3.10.2)
теңдеуімен анықталады.
Енді бойында тоғы бар өткізгіштің магнит өрісінде қозғалғанда істелетін жұмысты анықтайық.
Ұзындығы 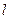 жылжымалы бөлігі бар контур біртекті магнит өрісінде болсын (3.3.10.1 – сурет).
жылжымалы бөлігі бар контур біртекті магнит өрісінде болсын (3.3.10.1 – сурет).  векторы сурет жазықтығына перпендикуляр және бізден суретке қарай бағытталған. Тоқ бағыты суретте көрсетілгендей
векторы сурет жазықтығына перпендикуляр және бізден суретке қарай бағытталған. Тоқ бағыты суретте көрсетілгендей 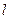 жылжымалы өткізгіш арқылы жоғарыдан төмен қарай бағытталсын.
жылжымалы өткізгіш арқылы жоғарыдан төмен қарай бағытталсын.
Бойында тоғы бар 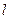 өткізгішке өріс тарапынан әсер етуші күш Ампер заңы бойынша F=IBl – ға тең. (бағыты сол қол ережесі бойынша анықталады). Осы күштің әсерінен l өткізгіш солдан оңға қарай жылжып бірінші жағдайдан екінші жағдайға келеді. Сонда өрістің істейтін жұмысы.
өткізгішке өріс тарапынан әсер етуші күш Ампер заңы бойынша F=IBl – ға тең. (бағыты сол қол ережесі бойынша анықталады). Осы күштің әсерінен l өткізгіш солдан оңға қарай жылжып бірінші жағдайдан екінші жағдайға келеді. Сонда өрістің істейтін жұмысы.
 (3.3.10.3)
(3.3.10.3)
болады, өйткені ldx=dS өткізгіш кесіп өтетін аудан, ал BdS =dФ осы ауданды тесіп өтуші магнит индукциясы векторының ағыны. Сонымен, бойында тоғы бар 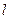 өткізгіш магнит өрісінде қозғалғанда істелетін жұмыс қозғалушы өткізгіш қиып өтетін магнит ағыны мен тоқтың көбейтіндісіне тең болады. Бұл формула
өткізгіш магнит өрісінде қозғалғанда істелетін жұмыс қозғалушы өткізгіш қиып өтетін магнит ағыны мен тоқтың көбейтіндісіне тең болады. Бұл формула  векторының кез келген бағыты үшін дұрыс болады.
векторының кез келген бағыты үшін дұрыс болады.

3.3.10.1 – сурет
Енді бойында тоғы бар контур магнит өрісінде қозғалғандағы жұмысты анықтайық. Айталық, М контур жылжып M1 жағдайына келсін (3.3.10.2 – сурет).
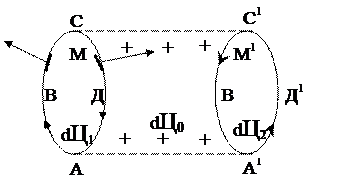
3.10.2 – сурет
Контурдағы тоқтың бағыты сағат тілінің бағытымен сәйкес келеді. Ал магнит өрісінің бағыты сурет жазықтығына перпендикуляр болсын. Контурды екі бөлікке, АВС және СДА, бөліп қарастырайық. Сонда Ампер күшінің АВС мен СДА өткізгіштерінің магнит өрісінде қозғалғандағы толық жұмысы dA=dA1 +dA2 болады. Контурдың СДА бөлігіне түсірілген күштер орын ауыстыру бағытымен сүйір бұрыштар жасайды, сондықтан оның істеген жұмысы dA2 >0 оң болады. Ол жұмыс (3.3.10.3) формуласы бойынша

болады. Бұл формуладағы dФ0 - (СДАА1В1С1) ауданын қиятын ағын, ал dФ2- контурдың соңғы қалпындағы (А1 Д 1С1 В1 С1) ауданын қиятын ағын.
Контурдың АВС бөлігіне әсер етуші күштер контурдың қозғалу бағытымен доғал бұрыштар жасайды. Сондықтан күштердің істеген жұмыстары dA1<0 теріс болады.
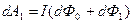
dФ1 ағыны (АВСДА) ауданын қияды. Сонымен толық жұмыс

мұндағы dФ2 – dФ1 =dФ1 – контур арқылы өтетін магнит ағынының өзгерісі. Сонда
 (3.3.10.4)
(3.3.10.4)
болады.
Сонымен, бойында тоғы бар тұйық контур магнит өрісінде орын ауыстырғанда істелген жұмыс тоқ пен контур арқылы өтетін магнит ағынының өзгерісінің көбейтіндісіне тең болады.
Егер контурды қиятын магнит ағыны өзгермесе орын ауыстыру жұмысы нольгеге тең болады. Мысалы, тоғы бар тұйық контурды біртекті магнит өрісінде ілгерілемелі қозғалысқа түсірсе, онда контурды қиятын магнит ағыны өзгермейді. Сондықтан қорытқы жұмыс нөлге тең болады.
3.3.11 Электромагниттік индукция құбылысы. Ленц ережесі
Кез келген тұйық өткізгіш контурмен шектелген ауданды қиып өтетін магнит ағыны өзгергенде контурда электр тоғы пайда болады. Бұл тоқты индукциялық тоқ, құбылысты электромагниттік индукция құбылысы деп атайды.
Электромагниттік индукция құбылысын 1831 жылы Фарадей ашты. Электромагниттік индукция құбылысын мынадай тәжірибелерден көруге болады:
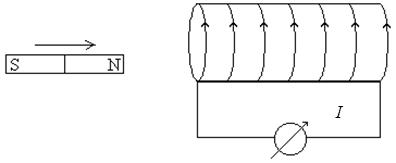
1) Гальванометрмен тұйықталған соленоид алып оған тұрақты магнитті жақындатайық (3.3.11.1 – сурет). Сонда соленоидта тоқ пайда болады.

ІІІ.3.27 – сурет
3.3.11.1 – сурет
Тоқтың пайда болғандығын гальванометр көрсетеді. Егер гальванометрді соленоидтан қашықтатсақ онда да алғашқы тоққа кері бағытта тоқ пайда болады. Дәл осындай жағдайлар магнитті қозғамай соленоидты магнитке жақындатса немесе алыстатса да байқалады. Егер магнитті де және соленоидты да қозғамаса тоқ болмайды және неғұрлым жылдам қозғалтсақ гальванометр стрелкасы көбірек ауытқиды.
2) Екі А және В соленоидтарын алып біреуін (А) гальванометрмен тұйықтап, ал екіншісін (В) тоқ көзі және К кілтпен тұйықтайық (3.3.11.2 – сурет).

3.3.11.2 – сурет
Егер К кілтпен В соленоидты тұйықтасақ, онда А соленоидында қысқа мерзімде тоқ пайда болады. Ал енді В соленоидындағы тізбекті ажыратсақ тағы да қысқа мерзімде тоқ пайда болады. Сонымен, А соленоидындағы тоқ В соленодындағы тіэбекті тұйықтау немесе ажырату мезетінде ғана байқалады.
Осы тәжірибелердің нәтижелеріне тоқталайық.
Бірінші тәжірибеде тұрақты магнитті соленоидқа жақындатқанда немесе алыстатқанда магнит өрісі өзгереді. Тоқ тек осы уақыттарда ғана пайда болады. Егер магниттің қозғалысын тоқтатсақ болды, контур маңындағы магнит өрісі өзгермейді, ендеше тоқта пайда болмайды. Дәл осындай құбылыс магнитті қозғамай, соленоидты магнитке жақындатқанда немесе алыстатқанда да болады. Екінші тәжірибеде магнит өрісінің өзгеруі В соленоидын тұйықтау немесе ажырату кезінде болады. Екі жағдайда да өткізгіш тұйық контурды қиятын магнит ағыны өзгергенде ғана контурда тоқ пайда болады екен. Егер өткізгіш тұйық контурды біртекті магнит өрісінде айналдырсақ, онда контурды қиятын магнит ағыны өзгереді де (жалпы магнит ағыны тұрақты) контурда индукциялық тоқ пайда болады. Индукциялық тоқтың бағытын анықтайық.– (3.3.11.1)- суреттегі бірінші тәжірибеде тұйық контурға магниттің солтүстік полюсін жақындатқанда соленоидтағы тоқ сағат тіліне қарса бағытталады. (магнит жағынан қарағанда). Бұл жағдайда тұрақты магниттің тудыратын магнит индукциясының ағыны сыртқа қарай бағытталады және соленоидқа жақындатқан сайын артады. Ал соленоидтағы индукциялық тоқтың тудыратын магнит индукциясының ағыны соленоидтан сыртқа қарай бағытталады (магнит қозғалысы бағытына қарай). Яғни, магниттің өрісінің артуына қарсы әсер жасайды. Ал магнитті соленоидтан алыстатқанда ондағы тоқ сағат тілімен бағыттас болады. мұның тудыратын магнит өрісі соленоид ішіне бағытталады. Магнитті қашықтатқанда тұрақты магниттің магнит өрісінің бағыты өзгермейді, бірақ магнит ағыны азая бастайды. Ендеше индукциялық тоқтың магнит өрісі тұрақты магниттің магнит өрісінің азаюына қарсы әсер жасайды. Сонымен, индукциялық тоқ өзінің магнит өрісі мен өзін тудыратын магнит өрісінің өзгеруіне қарсы әсер жасайтындай болып бағытталады. Яғни, соленоид маңындағы өріс арта бастаса, оны кемітуге ұмтылады, ал кеми бастаса, оны арттыруға ұмтылады. Бұны Ленц заңы деп атайды.
Қарастырылған тәжірибелерден тағы мынадай қорытынды жасауға болады. Cоленоидқа магниттің солтүстік полюсін жақындатқанда соленоидтың магнитке жақын жағынан солтүстік полюс пайда болады да магнит пен соленоид тебілісіке ұшырайды, яғни олардың арасында индукциялық тоқты тудырушы қозғалысқа қарсы әсер ететін күш пайда болады. Aл магниттің солтүстік полюсін соленоидтан қашықтата бастағанда соленоидтың магнитке жақын жағында оңтүстік полюс пайда болады. (3.3.11.3)-суретте осы айтылған мәселелер көрсетілген.

3.3.11.3-сурет
Магнит жақындағанда контурды қиятын магнит ағыны көбейе бастайды. Контурдағы индукциялық тоқ сағат тіліне қарсы бағытта болады, ал магнитті қашықтатқанда контурды қиятын магнит ағыны азая бастайды. Контурда пайда болған индукциялық тоқ сағат тілімен бағыттас болады. Индукциялық тоқтың тудыратын өрісі пунктирмен көрсетілген.
3.3.12 Фарадей заңы. Фарадей заңын энергияның сақталу заңы және электрондық теория бойынша шығару
Тұйық тізбек контурын өзгермелі магнит ағыны қиып өткенде контурда индукциялық тоқ пайда болады. Ал тоқ тудыру үшін электр қозғаушы күш (э.қ.к.) қажет. Сондықтан контурды қиятын магнит ағыны өзгергенде контурда индукциялық э.қ.қ. пайда болады деп есептеу керек. Осы э.қ.к-ін анықтайық. Ол үшін тоқ көзімен тұйықталған жылжымалы АС бөлігі бар тұйық тізбек алайық (3.3.12.1 – сурет).
Тізбектегі э.қ.к.  – нің жұмысы
– нің жұмысы  Джоуль–Ленц жылуына
Джоуль–Ленц жылуына 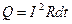 жұмсалады. Енді осы тізбек магнит өрісіне орналастырылсын. Өріс біртекті және бағыты өріс жазықтығына перпендикуляр болсын. Сонда тізбектің АС бөлігіне әсер етуші Ампер күші солға қарай бағытталады да dt уақыт ішінде өткізгіш A1 C1 жағдайына келеді. Бұл уақытта істелген жұмыс (3.3.10.3)-формуласы бойынша
жұмсалады. Енді осы тізбек магнит өрісіне орналастырылсын. Өріс біртекті және бағыты өріс жазықтығына перпендикуляр болсын. Сонда тізбектің АС бөлігіне әсер етуші Ампер күші солға қарай бағытталады да dt уақыт ішінде өткізгіш A1 C1 жағдайына келеді. Бұл уақытта істелген жұмыс (3.3.10.3)-формуласы бойынша  -ке тең болады. Mұндағы dФ (АСA1C1) ауданынан өтетін магнит индукциясының ағыны. Сонымен э.қ.қ.
-ке тең болады. Mұндағы dФ (АСA1C1) ауданынан өтетін магнит индукциясының ағыны. Сонымен э.қ.қ.  – нің толық жұмысы
– нің толық жұмысы
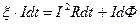 (3.3.12.1) Джоуль-Ленц жылуына және өткізгішті қозғауға жұмсалады.
(3.3.12.1) Джоуль-Ленц жылуына және өткізгішті қозғауға жұмсалады.

3.3.12.1 – сурет
Одан

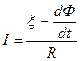
бұл теңдіктен индукцияның э.қ.к-ін табатын болсақ
 (3.3.12.2)
(3.3.12.2)
(3.3.12.2) теңдеу Фарадей заңы делінеді..
Сонымен Фарадей заңын былай тұжырымдауға болады: контурдағы э.қ.қ.– і 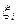 шама жағынан контурмен шектелген ауданды қиятын магнит ағынының өзгеріс жылдамдығына тең, таңба жағынан қарама – қарсы болады. Mагнит ағыны артқанда
шама жағынан контурмен шектелген ауданды қиятын магнит ағынының өзгеріс жылдамдығына тең, таңба жағынан қарама – қарсы болады. Mагнит ағыны артқанда  болады, яғни индукциялық тоқ өрісі ағынға қарсы бағытталады. Ағынның кемуінде
болады, яғни индукциялық тоқ өрісі ағынға қарсы бағытталады. Ағынның кемуінде  , яғни ағынның бағыты және индукциялық тоқ өрісінің бағыты бағыттас болады. (3.3.11.3-сурет). Сонымен Фарадей заңындағы минус таңбасы Ленц ережесінің математикалық пайымдалуы болып табылады.
, яғни ағынның бағыты және индукциялық тоқ өрісінің бағыты бағыттас болады. (3.3.11.3-сурет). Сонымен Фарадей заңындағы минус таңбасы Ленц ережесінің математикалық пайымдалуы болып табылады.
Енді индукция заңын электрондық теория тұрғысынан қарастырайық. АВ өткізгішін магнит өрісіне перпендикуляр жазықтықта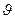 жылдамдықпен қозғайық (3.3.12.2 – сурет).
жылдамдықпен қозғайық (3.3.12.2 – сурет).
Магнит өрісінің индукция векторы сурет жазықтығына перпендикуляр және бізден суретке қарай бағытталсын. Сонда өткізгіштің еркін электрондарына әсер етуші Лоренц күші төмен 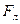 қарай бағытталады. Осы күштің әсерінен электрондар төмен қарай қозғала бастайды. Электрондарға осындай қозғалыс бере алатын электрлік күш F= eE, яғни
қарай бағытталады. Осы күштің әсерінен электрондар төмен қарай қозғала бастайды. Электрондарға осындай қозғалыс бере алатын электрлік күш F= eE, яғни
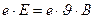
бұдан

болады.
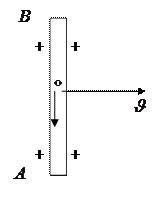
3.3.12.2 – сурет
мұнда 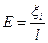 - электр өрісінің кернеулігі;
- электр өрісінің кернеулігі; 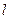 - өткізгіштің ұзындығы.
- өткізгіштің ұзындығы.
Бұл теңдіктерді салыстырып
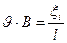
жазамыз да, эқ.қ.-ін анықтаймыз.
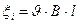
мұндағы 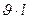 - өткізгіштің dt уақыт ішіндегі қиятын ауданы.
- өткізгіштің dt уақыт ішіндегі қиятын ауданы.
Сонымен
 (3.3.12.3)
(3.3.12.3)
э.қ.к.-інің формуласын алдық.
3.3.13 Контурдың индуктивтігі. Өзіндік индукция
Кез келген тұйық контурдағы электр тоғы өзінің айналасында магнит өрісін тудырады. Бұл өрістің магнит индукциясы тоққа пропорционал болады. Контурмен жүретін тоқ айнымалы болса, онда оның тудыратын магнит өрісі де айнымалы болады,. ендеше осы контурмен шектелген ауданды қиятын магнит ағыны да өзгермелі болады. Ал магнит индукциясының ағынының өзгеруі контурда индукциялық э.қ.к-ін тудырады. Осы құбылыс өзіндік индукция құбылысы делінеді.
Контурды қиып өтетін магнит ағыны осы контур арқылы жүретін тоққа пропорционал
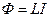 (3.3.13.1)
(3.3.13.1)
мұндағы L-контурдың индуктивтілігі делінеді. Индуктивтіліктің бірлігі  (Генри) болады.
(Генри) болады.
Шексіз ұзын соленоидтың индуктивтілігін анықтайық. Соленоидты қиып өтетін магнит ағынын (3.3.10.2) формула бойынша
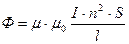
теңдігімен анықтауға болады. Осы формуланы (3.3.13.1) формуламен салыстырып
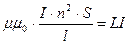
жазу нәтижесінде соленоидтың индуктивтілігін анықтауға болады
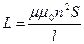 (3.3.13.2)
(3.3.13.2)
яғни, соленоидтың индуктивтілігі n соленоидтың орам санына, S көлденең қимасының ауданына және соленоидтың өзегі жасалған заттың 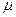 магниттілік өтімділігіне тәуелді.
магниттілік өтімділігіне тәуелді.
Өзіндік индукция құбылысына Фарадей заңын қолданып, өздік э.қ.к-і үшін мынадай теңдік жазуға болады
 (3.3.13.3)
(3.3.13.3)
Егер 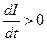 болса, онда
болса, онда , яғни өзіндік индукция тоғы негізгі тоққа қарсы бағытталады да, оның артуына кедергі жасайды. Ал егер
, яғни өзіндік индукция тоғы негізгі тоққа қарсы бағытталады да, оның артуына кедергі жасайды. Ал егер 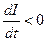 болса, онда
болса, онда , яғни индукциялық тоқ пен контурдағы кеми бастайтын негізгі тоқ бағыттас болады да, оның кемуін баяулатады. (3.3.13.3) формуласы бойынша 1с. ішінде өткізгіш арқылы өтетін тоқ 1 А-ге өзгергенде өткізгіште пайда болған 1В индукция э.қ.қ.-і өткізгіштің инлдуктивтігі 1 Гн делінеді.
, яғни индукциялық тоқ пен контурдағы кеми бастайтын негізгі тоқ бағыттас болады да, оның кемуін баяулатады. (3.3.13.3) формуласы бойынша 1с. ішінде өткізгіш арқылы өтетін тоқ 1 А-ге өзгергенде өткізгіште пайда болған 1В индукция э.қ.қ.-і өткізгіштің инлдуктивтігі 1 Гн делінеді.
3.3.14 Тізбектің тұйықталуы және ажыратылуы кезіндегі тоқтар
Контурдағы тоқтың кез-келген өзгеруі нәтижесінде өздік э.қ.қ.-і пайда болады да, контурда қосымша өздік индукцияның экстратоқтары деп аталатын қосымша тоқтар пайда болады. Ол Ленц ережесі бойынша тізбектегі тоқ көзі тудыратын тоққа қарама-қарсы бағытталады. Тоқ көзін ажыратқан кезде экстратоқтың бағыты әлсіреген тоқ бағытымен бағыттас болады. Сонымен, тізбекте индуктивтіктің болуы осы тізбекте тоқтың жоғалып кетуінін немесе орнығуын баяулатады.
Тізбектің ажыратылуы кезінде тоқтың өзгерісімен танысайық. Тізбекті ажыратқанда тізбектегі тоқ біртіндеп азаяды. Бұл уақытта контурмен шектелген ауданды қиятын магнит индукциясы ағыны кемитіндіктен контурда индукциялық тоқ пайда болады. Ленц заңы бойынша бұл тоқтың тудыратын магнит ағыны кемуші ағынды арттыруға ұмтылады. Яғни индукциялық тоқ бағытымен негізгі тоқ бағыттас келеді. Осы тоқты ажырату кезіндегі индукциялық тоқ деп атайды.
Э.қ.қк-і 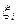 , индуктивтлігі L, кедергісі R болатын тізбекті қарастырайық (3.3.14.1-сурет).
, индуктивтлігі L, кедергісі R болатын тізбекті қарастырайық (3.3.14.1-сурет).

3.3.14.1-сурет
А ажыратқыш 1- ші жағдайда тұрғанда тізбектегі э.қ.қ-і  , тоқ
, тоқ  болсын. t=0 уақыт мезетінде контурды ажыратқышты 2- ші жағдайға әкеліп L катушка мен R кедеріні тұйықтайық. Сонда индуктивтік катушка арқылы жүрген тоқ кеми бастаған кезде, Ленц ережіне сәйкес тоқтың азаюына қарсы, өздік индукция э.қ.қ. – і пайда болады
болсын. t=0 уақыт мезетінде контурды ажыратқышты 2- ші жағдайға әкеліп L катушка мен R кедеріні тұйықтайық. Сонда индуктивтік катушка арқылы жүрген тоқ кеми бастаған кезде, Ленц ережіне сәйкес тоқтың азаюына қарсы, өздік индукция э.қ.қ. – і пайда болады

Кез-келген уақыт мезетінде тізбектегі тоқ Ом заңы бойынша анықталады

Бұл теңдікті
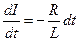
түрде жазуға болады. Осы теңдеуді I бойынша (I0-ден I-ге дейін) және t бойынша (0 -ден t-ға дейін) интегралдап

деп жазамыз немесе
 (3.3.14.1)
(3.3.14.1)
мұндағы тұрақты 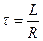 - релакция уақыты -. тоқ күшінің
- релакция уақыты -. тоқ күшінің 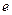 есе кемитін уақыты делінеді.
есе кемитін уақыты делінеді.
Сонымен тізбекті тоқ көзінен ажыратқанда тоқ экспоненциялды кемиді екен. Тоқтың уақытқа байланысты кемуі (3.3.14.1) – суретте 1-ші қисықпен көрсетілген. Тізбектің индуктивтілігі L неғұрлым үлкен болса, ал кедергісі неғұрлым аз болса соғұрлым t тұрақтысы үлкен болады: тізбекті ажыратқан кезде тоқ соғұрлым баяу кемиді.

3.3.14.1 - сурет
Енді тұйықталу тоғын қарастырайық. Тұйықталу кезінде сыртқы э.қ.к-і мен қатар тізбекте тоқтың артуына қарсы бағытталған өздік индукция э.қ.к-і пайда болады.
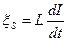
Ом заңы бойынша тізбектегі тоқ төмендегідей теңдікпен анықталады:

 деп белгілеу енгізген жағдайда
деп белгілеу енгізген жағдайда

І0 тұрақты болғандықтан 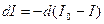 деп алуға болады.
деп алуға болады.
Сонда

болады.
t = 0 уақыт мезетінде I =0, ендеше I0 - I = I0. Бұл жағдайда тоқ үшін интегралдау шегі I0 -ден (I0-I)-ге дейін, уақыт үшін 0- ден t –ға дейін болады. Сонымен жоғарғы теңдеуді интегралдап

бұдан
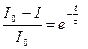
немесе
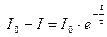
деп жазуға болады, мұндағы 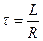 , ендеше
, ендеше
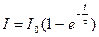 (3.3.14.2)
(3.3.14.2)
формуласын аламыз.
. Бұл формула тоқтың  тұрақты мәніне жеткенге дейін баяу артатындығын көрсетеді (3.3.14.1 – суреттегі 2-ші қисық).
тұрақты мәніне жеткенге дейін баяу артатындығын көрсетеді (3.3.14.1 – суреттегі 2-ші қисық).
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 2280; Нарушение авторских прав?; Мы поможем в написании вашей работы!