
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение на число, сложение, умножение матриц
|
|
|
|
Понятие матрицы. Виды матриц. Равенство матриц.
Конспект лекций по дисциплине
Филиал в г. ТУЛЕ
__________________________________________________________________
Кафедра математики и информатики
«Линейная алгебра»
(для студентов бакалавриата, обучающимся по направлениям 080199.62 «Экономика», 080500.62 «Бизнес-информатика»)
Составил: к.ф.-м.н., доцент
кафедры математики и информатики
Луценко Алексей Георгиевич
Рассмотрено и одобрено на заседании кафедры
кафедры математики и информатики
протокол № ___ от «___»____________ 2011 г.
Тема 1: Матрицы и определители
Транспонирование матрицы. Алгебраические операции над матрицами:
Определение 1. Матрицей размера m ´ n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
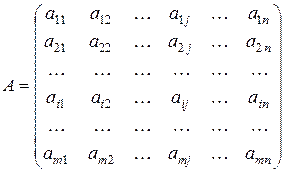 , ,
| aij - элемент матрицы A, где: i -номер строки, j - номер столбца. |
Определение 2. Две матрицы одного размера m ´ n называются равными, если они совпадают поэлементно, т.е. А = В Û aij = bij для любых i =1,2,..., m; j =1,2,..., n.
Определение 3. Матрица, состоящая из одной строки, называется матрицей-строкой A=(a 11, a 12,..., a 1n) или A=(a 1, a 2,..., a n).
| Матрица, состоящая из одного столбца, называется матрицей-столбцом: | 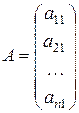 или или 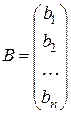 . .
|
Определение 4. Матрица называется квадратной матрицей n -го порядка, если число ее строк равно числу ее столбцов и равно n.
Определение 5. Элементы aij матрицы A, у которых номер строки i равен номеру столбца j, называются диагональными. Они образуют главную диагональ матрицы.
Квадратная матрица называется диагональной, если все недиагональные элементы равны нулю.
Определение 6. Единичной матрицей n -го порядка называется диагональная матрица n -го порядка, у которой все диагональные элементы равны 1.
Определение 7. Матрица любого размера называется нулевой, если все ее элементы равны 0.
Определение 8. Матрица  , которая получается из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице А.
, которая получается из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице А.
Из определения следует, что если матрица A имеет размер m ´ n, то транспонированная матрица A' имеет размер n ´ m.
Определение 9. Произведением матрицы A на число l называется матрица B=lA, элементы которой bij = laij для любых i =1,2,..., m; j =1,2,..., n.
Определение 10. Суммой двух матриц A и B одного размера называется матрица C=A + B, элементы которой сij = aij + bij для любых i =1,2,..., m; j =1,2,..., n.
Определение 11. Если число столбцов матрицы A равно числу строк матрицы B и равно k, то произведением матриц A и B называется матрица C=A × B, каждый элемент которой сij равен сумме произведений элементов i -ой строки матрицы A на соответствующие элементы j -го столбца матрицы B, т.е. сij = ai1b1j + ai2b2j +...+ aikbkj для любых i =1,2,..., m; j =1,2,..., n
Многие свойства операций над числами справедливы и для операций над матрицами (это проверяется по определению операций):
1) A+B=B+A;
2) (A+B)+C=A+(B+C);
3) l(A+B)=lA+lB;
4) A(BC)=(AB)C;
5) l(AB)=(lA)B=A(lB);
6) (A+B)C=AC+BC;
7) A(B+C)=AB+AC.
Однако для операций над матрицами справедливы не все свойства операций над числами. Например, AB ¹ BA для матриц 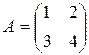 и
и 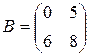 .
.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 457; Нарушение авторских прав?; Мы поможем в написании вашей работы!