Нулевой и тождественный операторы

Образ и прообраз векторов

Определение оператора. Понятие линейного оператора.

В евклидовом пространстве

Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса

Определение 1. Два вектора называются ортогональными, если их скалярное произведение равно нулю.

Определение 2. Базис линейного пространства e ₁, e ₂,..., e _n называется ортогональным, если (e _i, e _j)=0 при всех i ≠ j.

Определение 3. Базис линейного пространства e ₁, e ₂,..., e _n называется ортонормированным, если эти векторы попарно ортогональны и норма каждого из них равна единице, то есть (e _i, e _j)=0 при всех i ≠ j и ç e _i ç=1 при i = 1, 2, …, n.

Теорема 1. Во всяком n - мерном евклидовом пространстве существует ортонормированный базис (без доказательства).

Тема 4: Линейные операторы

Определение 1. Если задан закон (правило), по которому каждому вектору x = (x ₁, x ₂, … x _n) пространства R ⁿ ставится в соответствии единственный вектор y = (y ₁, y ₂, … y _m) пространства R ^m, то говорят, что задан оператор (преобразование, отображение), действующий из R ⁿ в R ^m и записывают y = A (x).

Определение 2. Оператор называется линейным, если для любых векторов x и y пространства R ⁿ и любого числа a выполняются соотношения:

1) A (x + y) = A (x) + A (y) – свойство аддитивности оператора;

2) A (a × x) = a × A (x) – свойство однородности оператора.

Определение 3. Вектор y = A (x) называется образом вектора x, а сам вектор x - прообразом вектора y.

20. Матрица линейного оператора в заданном базисе: связь между вектором х и образом у. Ранг оператора. Операции над линейными операторами.

Рассмотрим далее отображение линейного пространства R ⁿ в себя. Зафиксируем базис e ₁, e ₂,..., e _n этого пространства.

Связь между вектором x и его образом A (x) можно выразить в матричной форме уравнением Y = A ×X, где A – матрица линейного оператора A в заданном базисе, X = (x ₁, x ₂, … x _n)¢, Y = (y ₁, y ₂, … y _n)¢ - матрицы-столбцы из координат векторов x и y.

Теорема 1. Каждому линейному оператору линейного пространства R ⁿ в себя соответствует матрица в данном базисе. Обратно, всякой матрице n - го порядка соответствует линейный оператор n-мерного пространства.

Доказательство основано на теореме о единственности разложения вектора линейного пространства по базису и свойствах аддитивности и однородности линейного оператора.

Пусть x = x ₁ e ₁+ x ₂ e ₂+... + x _n e _n. Тогда A (x) = x ₁ A (e ₁) + x ₂ A (e ₂) +... + x _n A (e _n) = = x ₁(a ₁₁ e ₁+ a ₂₁ e ₂+…+ a _n1 e _n)+ x ₂(a ₁₂ e ₁+ a ₂₂ e ₂+…+ a _n2 e _n)+... + x _n(a _1n e ₁+ a _2n e ₂+…+ a _nn e _n) =

= (a ₁₁ x ₁+ a ₁₂ x ₂ +…+ a _1n x _n) e ₁+ (a ₂₁ x ₁+ a ₂₂ x ₂ +…+ a _2n x _n) e ₂+ (a _n1 x ₁+ a _n2 x ₂ +…+ a _nn x _n) e _n.

С другой стороны, y = y ₁ e ₁+ y ₂ e ₂+... + y _n e _n.

Следовательно,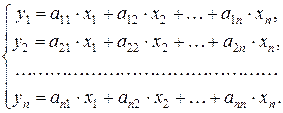

Определение 1. Ранг матрицы A называется рангом оператора A.

Определение 2. Суммой двух линейных операторов A и B называется оператор (A + B), определяемый равенством (A + B)(x) = A (x) + B (x).

Определение 3. Произведением линейного оператора A на число l называется оператор l A, определяемый равенством l A (x) =l(A (x)).

Определение 4. Произведением двух линейных операторов A и B называется оператор (AB), определяемый равенством (AB)(x) = A (B (x)).

Определение 5. Нулевым оператором называется оператор, переводящий все векторы пространства R ⁿ в нулевые векторы.

Определение 6. Тождественным оператором называется оператор E, переводящий каждый вектор в себя, то есть E (x) = x.

Дата добавления: 2014-11-06