Основы расчета систем с постоянными магнитами

КАТУШКИ ЭЛЕКТРОМАГНИТОВ

Катушка является одним из главных элементов электромагнита и должна удовлетворять следующим основным требованиям:

1) обеспечивать надежное включение электромагнита при наихудших условиях, т.е. в нагретом состоянии и при пониженном напряжении;

2) не перегреваться свыше допустимой температуры при всех возможных режимах, т. е. при повышенном напряжении;

3) при минимальных размерах быть удобной для производства;

4) быть механически прочной;

5) иметь определенный уровень изоляции, а в некоторых аппаратах быть влаго-, кислотно- и маслостойкой.

В процессе работы в катушке возникают напряжения: механические – за счет электродинамических сил в витках и между витками, особенно при переменном токе; термические – за счет неравномерного нагрева отдельных ее частей; электрические – за счет перенапряжений, в частности при отключении.

При расчете катушки необходимо выполнить два условия. Первое – обеспечить требуемую МДС при горячей катушке и пониженном напряжении. Второе – температура нагрева катушки при этом не должна превосходить допустимую.

В результате расчета должны быть определены следующие величины, необходимые для намотки: d – диаметр проволоки выбранной марки; w – число витков; R – сопротивление катушки.

По конструктивному исполнению различают катушки: каркасные – намотка осуществлена на металлическом или пластмассовом каркасе; бескаркасные бандажированные – намотка производится на съемном шаблоне, после намотки катушка бандажируется; бескаркасные с намоткой на сердечник магнитной системы.

Постоянный магнит представляет собой кусок стали или какого-либо другого твердого сплава, который, будучи намагничен, устойчиво сохраняет, запасенную часть магнитной энергии. Назначение магнита – служить источником магнитного поля, не меняющимся заметно ни со временем, ни под влиянием таких факторов, как сотрясения, изменение температуры, внешние, магнитные поля. Постоянные магниты применяются в разнообразных устройствах и приборах: реле, электроизмерительных приборах, контакторах, электрических машинах.

Различают следующие основные группы сплавов для постоянных магнитов:

1) мартенситовые стали – углеродистые, вольфрамовые, хромистые, кобальтовые;

2) сплавы на основе стали – никеля – алюминия с добавлением в некоторых случаях кобальта, силиция: альни (Fe, Al, Ni), альниси (Fe, Al, Ni, Si), магнико (Fe, Ni, Al, Co);

3) сплавы на основе серебра, меди, кобальта.

Величинами, характеризующими постоянный магнит, являются остаточная индукция В _r и коэрцитивная сила Н _c. Для определения магнитных характеристик готовых магнитов пользуются кривыми размагничивания (рис. 7-14), представляющими собой зависимость В = f (– H). Кривая снимается для кольца, которое вначале намагничивается до индукции насыщения, а затем размагничивается до В = 0.

Поток в воздушном зазоре. Для использования энергии магнита необходимо изготовить его с воздушным зазором. Составляющая МДС, затрачиваемая постоянным магнитом на проведение потока в воздушном зазоре, называется свободной МДС.

Наличие воздушного зазора δ снижает индукцию в магните от В _r до В (рис. 7-14) аналогично тому, как если бы по катушке, надетой на кольцо, пропустили размагничивающий ток, создающий напряженность H. Это соображение положено в основу приведенного ниже способа вычисления потока в воздушном зазоре магнита.

При отсутствии зазора вся МДС расходуется на проведение потока через магнит:

(7-34)

где l _μ – длина магнита.

При наличии воздушного зазора часть МДС F _δ будет расходоваться на проведение потока через этот зазор:

F = F _μ + F _δ (7-35)

Допустим, что мы создали такую размагничивающую напряженность магнитного поля Н, что

Н l _μ = F _δ (7-36)

и индукция при этом стала В.

При отсутствии рассеяния поток в магните равен потоку в воздушном зазоре

Bs _μ = F _δΛ_δ = Λ l _μΛ_δ, (7-37)

где s _μ – сечение магнита; Λ_δ = μ₀ s _δ /δ; μ₀ – магнитная проницаемость воздушного зазора.

Из рис. 7-14 следует, что

B/H = l _μ Λ_δ/ s_μ = tg α (7-38)

Рис. 7-14. Кривые размагничивания

Таким образом, зная данные о материале магнита (в виде кривой размагничивания), размеры магнита l _μ, s _μ и размеры зазора δ, s _δ, можно, пользуясь уравнением (7-38), вычислить поток в зазоре. Для этого следует провести на диаграмме (рис. 7-14) прямую Ob под углом α. Отрезок bс определяет индукцию В магнита. Отсюда поток в воздушном зазоре будет

(7-39)

При определении tg α учитываются масштабы оси ординат и абсцисс:

(7-40)

где р = n/m — отношение масштабов осей В и H.

С учетом рассеяния поток Ф_δ определяется следующим образом.

Проводят прямую Ob под углом α, где tg α == Λ_δ l _μ (ps _μ). Полученное значение В характеризует индукцию в среднем сечении магнита. Поток в среднем сечении магнита

(7-41)

Поток в воздушном зазоре

(7-42)

де σ — коэффициент рассеяния. Индукция в рабочем зазоре

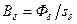(7-43)

Прямые магниты. Выражение (7-42) дает решение задачи для магнитов замкнутой формы, где проводимости воздушных зазоров могут быть вычислены с достаточной для практических целей точностью. Для прямых магнитов задача вычисления проводимостей потока рассеяния весьма трудна. Поток вычисляется с помощью опытных зависимостей, связывающих напряженность поля магнита с размерами магнита [20].

Свободная магнитная энергия. Это та энергия, которую отдает магнит в воздушных зазорах. При расчете постоянных магнитов, выборе материала и требуемых соотношений размеров стремятся к максимальному использованию материала магнита, сводящемуся к получению максимального значения свободной магнитной энергии.

Магнитная энергия, сосредоточенная в воздушном зазоре, пропорциональная произведению потока в зазоре и МДС:

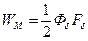(7-44)

Учитывая, что

(7-45)

Получаем

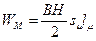(7-46)

где V— объем магнита. Материал магнита характеризуется магнитной энергией, отнесенной к единице его объема.

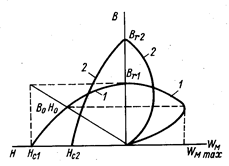
Рис. 7-15. К определению магнитной энергии магнита

Пользуясь кривой размагничивания, можно построить кривую W _м = f (В) при V = 1 (рис. 7-15). Кривая W _м = f (В) имеет максимум при каких-то значениях В и H, которые обозначим В ₀ и H ₀. Практически применяется способ нахождения В ₀ и H ₀ без построения кривой W _м = f (В). Точка пересечения диагонали четырехугольника, стороны которого равны В _r и Н _c, с кривой размагничивания достаточно близко соответствует значениям В ₀, Н ₀. Остаточная индукция В_r колеблется в относительно малых пределах (1-2,5), а коэрцитивная сила Н_c – в больших (1 – 20). Поэтому различают материалы: низкокоэрцитивные, у которых W _м малое (кривая 2), высококоэрцитивные, у которых W _м большое (кривая 1).

Кривые возврата. В процессе работы может меняться воздушный зазор. Допустим, что до введения якоря индукция была B ₁tg a ₁. При введении якоря зазор δ изменяется, и такому состоянию системы соответствует угол а ₂; (рис. 7-16) и большая индукция. Однако увеличение индукции происходит не по кривой размагничивания, а по некоторой другой кривой b ₁ cd, названной кривой возврата. При полном замыкании (δ = 0) мы имели бы индукцию B ₂. При изменении зазора в обратном направлении индукция меняется по кривой dfb ₁. Кривые возврата b ₁ cd и dfb ₁ являются кривыми частных циклов намагничивания и размагничивания. Ширина петли обычно невелика, и петлю можно заменить прямой b₁d. Отношение Δ В /Δ Н называется обратимой проницаемостью магнита.

Старение магнитов. Под старением понимают явление уменьшения магнитного потока магнита с течением времени. Это явление определяется рядом причин, перечисляемых ниже.

Структурное старение. Материал магнита после закалки или отливки имеет неравномерную структуру. Со временем эта неравномерность переходит в более стабильное состояние, что приводит к изменению значений В и Н.

Механическое старение. Происходит вследствие ударов, толчков, вибраций и влияния высоких температур, которые ослабляют поток магнита.

Магнитное старение. Определяется влиянием внешних магнитных полей.

Стабилизация магнитов. Всякий магнит перед установкой его в аппарат должен быть подвергнут дополнительному процессу стабилизации, после которого увеличивается сопротивляемость магнита уменьшению потока.

Структурная стабилизация. Заключается в дополнительной термической обработке, которая проводится до намагничивания магнита (кипячение закаленного магнита в течение 4 ч после закалки). Сплавы на основе стали, никеля и алюминия не требуют структурной стабилизации.

Механическая стабилизация. Намагниченный магнит подвергается перед установкой в аппарат ударам, сотрясениям, вибрации в условиях, близких режиму работы.

Магнитная стабилизация. Намагниченный магнит подвергают действию внешних полей переменного знака, после чего магнит становится более устойчивым к воздействию внешних полей, к температурным и механическим воздействиям.

ГЛАВА 8 ЭЛЕКТРОМАГНИТНЫЕ МЕХАНИЗМЫ

Дата добавления: 2014-10-15