
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Где аргументом является время t
|
|
|
|
СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
В курсе теоретической механики обычно изучаются движение точки и твердого тела. Соответственно кинематика делится на кинематику точки и кинематику твердого тела.
Механическое движение происходит в пространстве при изменении времени. Пространство в теоретической механике считается евклидовым, не зависящим от времени и движущихся в нем материальных тел. Время предполагается универсальным, т.е. одинаковым во всех системах отсчета и не зависящим от движения одной системы относительно другой
ВВЕДЕНИЕ
Кинематика – это раздел теоретической механики, в котором изучается движение материальных тел (точки) без рассмотрения причин, вызывающих или изменяющих это движение. Такое изучение движения материальных тел не требует учета их масс и действующих на них сил.
Под механическим движением материальных тел понимают происходящее с течением времени изменение их относительного положения в пространстве или взаимного положения частей данного тела. Движение материального тела всегда следует рассматривать относительно какого-либо другого тела – тела отсчета. С телом отсчета скрепляют систему осей координат, например декартовых, принимая ее за систему отсчета, относительно которой рассматривается движение материального тела.
1. КИНЕМАТИКА ТОЧКИ
В кинематике точки рассматриваются две задачи: 1) установление математических способов задания движения точки относительно выбранной системы отсчета; 2) определение по заданному закону движения точки всех кинематических характеристик этого движения (траектории точки, а также ее скорости и ускорения в любой момент времени).
Геометрическое место последовательных положений движущейся точки относительно рассматриваемой системы отсчета называется траекторией точки. Если траектория – прямая линия, то движение точки называется прямолинейным, если траектория – кривая линия, то к риволинейным.
Задать движение точки – это значит указать такой способ, при помощи которого можно определить положение точки в каждый момент времени относительно выбранной системы координат. Существуют три наиболее распространенных способа задания движения точки: векторный, координатный и естественный. Векторный способ применяется главным образом при изучении теоретических вопросов, а координатный и естественный – при решении различных практических задач.
Векторный способ задания движения.
Пусть точка M движется относительно выбранной системы координат по траектории AB (рис.1). Построим вектор  =
=  , соединяющий начало координат О с движущейся точкой М. Этот векторназывается радиус-вектором точки М. Положение движущейся точки М относительно фиксированной точки О системы отсчета будет полностью определено, если в каждый момент времени будут известны модуль и направление ее радиус-вектора относительно точки О. Таким образом движение точки М задается векторной функцией
, соединяющий начало координат О с движущейся точкой М. Этот векторназывается радиус-вектором точки М. Положение движущейся точки М относительно фиксированной точки О системы отсчета будет полностью определено, если в каждый момент времени будут известны модуль и направление ее радиус-вектора относительно точки О. Таким образом движение точки М задается векторной функцией

 =
=  (t), (1.1)
(t), (1.1)
Это равенство называется векторным уравнением движения точки или законом движения точки в векторной форме.
Линия, образованная концами переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора. Следовательно, траектория точки М является годографом ее радиус- вектора  .
.
Координатный способ задания движения.
Пусть точка О является началом прямоугольной декартовой системы координат Oxyz, и пусть 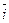 ,
,  ,
, 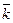 – единичные векторы осей x,y, z соответственно (рис.2).
– единичные векторы осей x,y, z соответственно (рис.2).
 Тогда радиус-вектор точки М относительно начала отсчета – точки О может быть выражен через его проекции на оси x, y, z:
Тогда радиус-вектор точки М относительно начала отсчета – точки О может быть выражен через его проекции на оси x, y, z:
 = rx
= rx 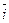 + ry
+ ry  + rz
+ rz 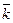 .
.
Но проекции радиус-вектора равны координатам точки М: rx = x, ry = y, rz =z. Поэтому модуль и направление радиус-вектора
 = x
= x 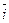 + y
+ y  + z
+ z 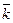 (1.2)
(1.2)
будут определены, если в каждый момент времени известны координаты точки М, т.е. если заданы три равенства
x = f1(t), y = f2(t), z = f3(t). (1.3)
Эти уравнения полностью определяют в каждый момент времени положение точки относительно выбранной системы координат и называются уравнениями илизаконом движения точки в координатной форме.
Уравнения движения (1.3) есть также уравнения траектории точки в параметрической форме. Параметром является время t. Чтобы получить уравнение траектории в координатной форме, надо из них исключить параметр t.
Естественный способ задания движения.
Естественным способом задания движения удобно пользоваться в тех случаях, когда заранее известна траектория движущейся точки. Пусть точка М движется по траектории АВ (рис.3), заданной или ее уравнениями, или каким либо геометрическим способом. Выберем на этой траектории какую-нибудь неподвижную точку О, которую примем за начало отсчета, и установим на траектории положительное и отрицательное направление отсчета, превратив тем самым траекторию в криволинейную ось s. Тогда положение точки М на траектории будет однозначно определяться криволинейной (натуральной) координатой
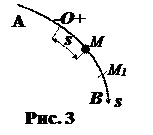 s, которая равна расстоянию от точки О до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. Чтобы знать положение точки на траектории в любой момент времени надо знать зависимость
s, которая равна расстоянию от точки О до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. Чтобы знать положение точки на траектории в любой момент времени надо знать зависимость
s = f(t). (1.4)
Уравнение (1.4) и выражает закон движения точки М вдоль траектории.
Таким образом, при естественном способе задаются:
1) траектория, 2) начало отсчета (точка О) криволинейной координаты s,
положительное и отрицательное направления отсчета (направление роста и убывания) криволинейной координаты s, 4) закон изменения криволинейной координаты s = f(t).
Криволинейную координату точки s не следует смешивать с длиной пути S, пройденного движущейся точкой за некоторый промежуток времени. Например, если точка, двигаясь из начала О, доходит до положения М1 (рис.3), а затем, перемещаясь в обратном направлении, приходит в положение М, то в этот момент времени ее криволинейная координата s = OM, а пройденный за время движения путь S = OM1 + M1M, т. е. не равен s.
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 583; Нарушение авторских прав?; Мы поможем в написании вашей работы!