Положение вращающегося тела в каждый момент времени будет известно, если задана

зависимость угла поворота от времени:

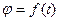. (2.2)

Уравнение (2.2) называется уравнением или законом вращения твердого дела вокруг неподвижной оси.

Измеряется угол φ в радианах; угол поворота φ в радианах, соответствующий N оборотам равен

.

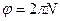Угловая скорость и угловое ускорение тела.

Для характеристики вращательного движения твердого тела вокруг неподвижной оси введем понятия угловой скорости и углового ускорения.

Угловая скорость характеризует быстроту изменения угла поворота φ с течением времени.

Алгебраической угловой скоростью тела в какой либо момент времени называют первую производную по времени от угла поворота в этот момент, т. е. 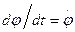.Условимся абсолютное значение угловой скорости обозначать ω, а алгебраическую угловую скорость ω_z. Тогда

ω_z = 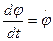(2.3)

Знак алгебраической угловой скорости показывает направление вращения тела. Если ω_z = 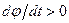, то угол поворота возрастает, и вращение происходит в сторону роста угла поворота, т. е. против часовой стрелки. Если ω_z = 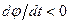, то угол поворота убывает, и тело вращается по часовой стрелке.

Угловая скорость измеряется в рад/с, об/мин и т. д. Если тело совершает n об/мин, то соответствующая угловая скорость в рад/с определяется по формуле

.

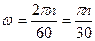Угловое ускорение тела характеризует быстроту изменения угловой скорости с течением времени.

Алгебраическим угловым ускорением тела называют первую производную по времени от алгебраической угловой скорости, т. е. вторую производную от угла поворота . Условимся абсолютное значение углового ускорения обозначать ε, а алгебраическое угловое ускорение 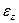. Тогда

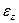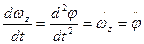= (2.4)

Измеряется угловое ускорение в рад/с²=с^-2.

Сравнивая знак алгебраического углового ускорения 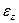со знаком алгебраической угловой скорости 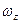, можно установить, является ли вращение тела в данный момент времени ускоренным, или замедленным, и в какую сторону оно при этом вращается.

—Если и 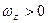, то величина алгебраической угловой скорости возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент в сторону роста угла поворота (против часовой стрелки).

Если 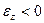и , то тело вращается ускоренно в сторону убывания угла поворота (по часовой стрелке).

Если 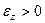и , то тело вращается замедленно в сторону убывания угла поворота (против часовой стрелки).

Есл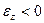и и 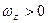, то тело вращается замедленно в сторону роста угла поворота (по часовой стрелке).

Отсюда видно, что если знак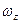и и 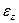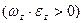одинаковые, то вращение тела ускоренное, если разные , то замедленное.

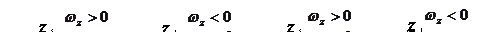На рисунках угловую скорость и угловое ускорение часто изображают дуговыми стрелками вокруг оси вращения (рис.15).

Дуговая стрелка для угловой скорости указывает направление вращения тела. Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления (рис.15,а), для замедленного—их направления противоположны (рис.15,б).

Частные случаи вращения твердого тела

Вращение твердого тела называется равномерным в течение некоторого промежутка времени, если в течение этого промежутка времени величина угловой скорости ω постоянна.

Вращение твердого тела называется равнопеременным в течение некоторого промежутка времени, если в течение этого промежутка времени величина углового ускорения ε постоянна. При этом если абсолютная величина угловой скорости увеличивается, вращение называется равноускоренным, а если уменьшается – равнозамедленным. Скорости и ускорения точек тела.

Рассмотрим точку M твердого тела, находящуюся на расстоянии h от оси вращения (рис.14). При вращении тела точка M будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр C лежит на этой оси. На рис.16 показана траектория точки M, где точка C– след оси вращения, OC– след неподвижной плоскости P, а MC– подвижной плоскости Q. Расстояние s точки M по дуге

окружности (траектории точки) от неподвижной точки O выражается зависимостью

.

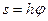Получили, что движение точки M задано естественным способом. Определяем скорость и ускорение точки M.

Алгебраическая скорость

= .

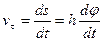Модуль скорости точки

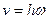. (2.7)

Скорость v в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.

Таким образом, модуль вектора скорости точки вращающегося твердого тела равен произведению абсолютного значения угловой скорости тела на расстояние от этой точки до оси вращения.

Направлен вектор скорости по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М, в сторону вращения тела. Здесь следует напомнить, что направление вращения определяет знак .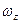

Ускорение точки разлагаем на касательную и нормальную составляющие, т. е.

.

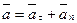Касательное и нормальное ускорения вычисляем по формулам

, .

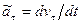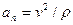В нашем случае 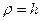. Тогда

, .

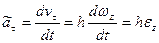Модуль вектора касательного ускорения точки вращающегося тела равен произведению абсолютного значения углового ускорения на расстояние от этой точки до оси вращения, т. е.

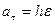. (2.8)

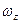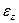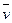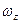Направление касательного ускорения зависит от знаков алгебраической скорости и алгебраического касательного ускорения. Если знаки и одинаковые (), т. е. вращение тела ускоренное, то направления векторов и совпадают. Если знаки и 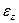разные (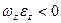), т. е. вращение тела замедленное, то направления векторов 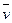и противоположны.

Модуль вектора нормального ускорения точки вращающегося тела равен отношению квадрата скорости к радиусу окружности, т. е.

. (2.9)

Нормальное ускорение направлено по радиусу МС окружности к оси вращения (рис. 16).

Полное ускорение точки М

.

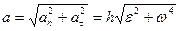Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом α, который вычисляется по формуле

.

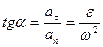Векторы угловой скорости и углового ускорения.

Введем понятия векторов угловой скорости и углового ускорения тела.

Вектором угловой скорости тела, вращающегося вокруг неподвижной оси, называется вектор, модуль которого равен абсолютному значению алгебраической угловой скорости, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против часовой стрелки.

Если —единичный вектор оси вращения z, направленный в ее положительную сторону, то вектор угловой скорости можно определить по формуле

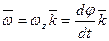. (2.10)

Из этой формулы следует, что при 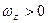направление вектора совпадает с направлением единичного вектора , а при вектор направлен в сторону, противоположную направлению вектора .

Вектором углового ускорения тела, вращающегося вокруг неподвижной оси, называется вектор, равный производной по времени от вектора угловой скорости, т. е.

. (2.11)

Очевидно, что вектор 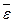направлен, как и вектор , вдоль оси вращения.

Из формул (2.10) и (2.11) следует, что алгебраическая угловая скорость 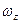и алгебраическое угловое ускорение 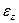представляют проекции векторов угловой скорости и углового ускорения 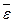на ось вращения, т. е.

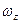пр_z = , пр_z = .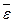

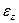Векторы и 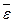можно изображать в любых точках оси вращения. Они являются векторами скользящими. При ускоренном вращении тела, т. е. когда 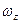и 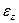имеют одинаковые знаки (), направления векторов угловой скорости и углового ускорения 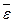совпадают (рис.15,а). Если вращение тела замедленное, 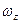и 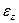имеют разные знаки (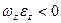), то направления векторов и 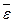противоположны (рис.15,б).

Дата добавления: 2014-11-06