
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Скорость точки 1 страница
|
|
|
|
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Она характеризует, как быстро и в каком направлении меняется направление перемещения точки.
Определение скорости при векторном способе задания движения.
Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть в момент времени t движущаяся точка находится в
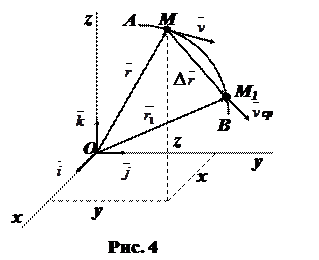 положении М, определяемом радиус-вектором
положении М, определяемом радиус-вектором  , а в момент времени t1 приходит в положение М1, определяемое вектором
, а в момент времени t1 приходит в положение М1, определяемое вектором 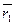 (рис.4). Тогда перемещение точки за промежуток времени ∆ t = t1–t определяется вектором ∆
(рис.4). Тогда перемещение точки за промежуток времени ∆ t = t1–t определяется вектором ∆  =
=  , который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно, и вдоль самой траектории, если движение является прямолинейным. Из треугольника ОММ1 видно, что
, который будем называть вектором перемещения точки. Этот вектор направлен по хорде, если точка движется криволинейно, и вдоль самой траектории, если движение является прямолинейным. Из треугольника ОММ1 видно, что
∆  =
= 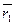 –
–  .
.
Отношение вектора перемещения ∆  к промежутку времени ∆ t, в течение которого произошло это перемещение, называется средней скоростью точки М за промежуток времени ∆ t:
к промежутку времени ∆ t, в течение которого произошло это перемещение, называется средней скоростью точки М за промежуток времени ∆ t:
 cp =
cp = 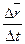 .
.
Этот вектор направлен так же, как и ∆  , т. е. вдоль хорды ММ1.
, т. е. вдоль хорды ММ1.
Очевидно, что чем меньше промежуток времени ∆ t, для которого вычислена средняя скорость, тем величина  cp будет точнее характеризовать движение точки. Чтобы получить точную характеристику движения вводят понятие о скорости точки в данный момент времени.
cp будет точнее характеризовать движение точки. Чтобы получить точную характеристику движения вводят понятие о скорости точки в данный момент времени.
Скорость точки в данный момент времени t называется векторная величина  , к которой стремится средняя скорость
, к которой стремится средняя скорость  ср при стремлении промежутка времени ∆ t к нулю:
ср при стремлении промежутка времени ∆ t к нулю:
 =
=  (
(  cp) =
cp) = 
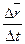 . (1.5)
. (1.5)
Так как ∆ t – приращение скалярного аргумента t, а ∆  – приращение вектора-функции
– приращение вектора-функции  , то предел отношения ∆
, то предел отношения ∆  /∆ t при ∆ t→ 0 является векторной производнойот
/∆ t при ∆ t→ 0 является векторной производнойот  по t и обозначается, как и производная от скалярной функции, символом
по t и обозначается, как и производная от скалярной функции, символом  / dt:
/ dt:

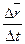 =
= 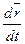 . (1.6)
. (1.6)
Из равенств (1.5) и (1.6) следует:
Вектор скорости точки в данный момент времени равен векторной или геометрической производной радиус вектора точки по времени:
 =
= 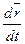 =
=  . (1.7)
. (1.7)
Здесь производная по времени, следуя И.Ньютону, обозначена точкой ( ).
).
При стремлении ∆ t хорда ММ1, а следовательно и вектор средней скорости  ср, поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе совпадает с ней. Поэтому вектор скорости точки
ср, поворачивается вокруг точки М, приближаясь к касательной к траектории в точке М и в пределе совпадает с ней. Поэтому вектор скорости точки  направлен по касательной к траектории точки в сторону движения. Размерность скорости L/T, т. е. длина/время; единицами измерения могут быть м/с, см/с, км/ч.
направлен по касательной к траектории точки в сторону движения. Размерность скорости L/T, т. е. длина/время; единицами измерения могут быть м/с, см/с, км/ч.
Замечание. При рассмотрении задач кинематики и динамики приходится часто встречаться с векторами, имеющими различный физический смысл и являющимися функциями различных скалярных аргументов (времени, дуги и пр.) Такие векторы называются вектор функциями скалярного аргумента. Годографом вектор функции скалярного аргумента называется кривая, которую описывает конец переменного вектора, если его начало совместить с неподвижной точкой. Как было показано в п.1.1, радиус-вектор движущейся точки  =
=  (t), является вектор функцией скалярного аргумента t, годограф этой вектор функции – траектория движущейся точки. При вычислении скорости движущейся точки было применено определение векторной или геометрической производной от векторной функции
(t), является вектор функцией скалярного аргумента t, годограф этой вектор функции – траектория движущейся точки. При вычислении скорости движущейся точки было применено определение векторной или геометрической производной от векторной функции  по скалярному аргументу t. Определение скорости при координатном способе задания движения.
по скалярному аргументу t. Определение скорости при координатном способе задания движения.
Пусть движение точки задано в прямоугольной декартовой системе координат Oxyz (рис.4), принятой за неподвижную, т. е. пусть заданы координаты точки как функции времени (1.3):
x = f1(t), y = f2(t), z = f3(t).
Согласно выражению (1.2)
 = x
= x 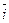 + y
+ y  + z
+ z 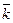 .
.
Скорость точки равна производной радиус-вектора точки по времени – формула (1.7). Найдем эту производную, учитывая, что орты 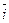 ,
,  ,
, 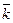 постоянны по величине и направлению и могут быть вынесены за знак производной:
постоянны по величине и направлению и могут быть вынесены за знак производной:
 =
= 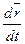 =
= 
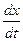 +
+ 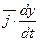 +
+ 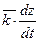 . (1.8)
. (1.8)
Разложение вектора скорости точки по ортам декартовой системы координат имеет вид:
 =
= 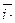 vx +
vx + 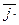 vy +
vy +  vz, (1.9)
vz, (1.9)
где сомножители при ортах vx, vy, vz – проекции вектора  на соответствующие оси координат.
на соответствующие оси координат.
Сравнивая (1.8) и (1.9), получаем для проекций вектора скорости на декартовые оси координат следующие формулы:
vx = 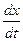 =
= 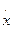 , vy =
, vy = 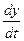 =
=  , vz =
, vz = 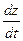 =
= 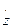 . (1.10)
. (1.10)
Следовательно, проекции вектора скорости точки на координатные оси равны первым производным по времени от соответствующих координат этой точки.
По проекциям вектора скорости определяем числовое значение (модуль) скорости и косинусы углов вектора скорости с осями координат (направляющие косинусы):
v = 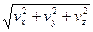 . (1.11)
. (1.11)
cos( ,
, 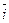 ) = vx / v; cos(
) = vx / v; cos( ,
,  ) = vy / v; cos(
) = vy / v; cos( ,
, 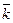 ) = vz / v. (1.12)
) = vz / v. (1.12)
Определение скорости при естественном способе задания движения.
Пусть движение точки задано естественным способом, т. е. известны ее траектория АВ, начало и направление отсчета криволинейной координаты и уравнение движения точки s = f (t) (рис.5). В момент времени t точка занимает положение М, а в момент t1 =t + ∆t – положение М1. За время ∆t радиус-
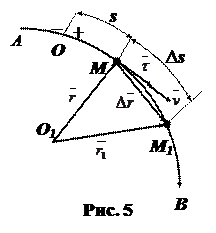 вектор точки М получилприращение
вектор точки М получилприращение  , а криволинейная координата s – приращение ∆ s.
, а криволинейная координата s – приращение ∆ s.
На основании (1.5)
 =
= 
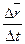 .
.
Перепишем это равенство в виде:
 =
= 
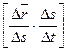 =
= 
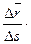

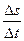 =
=  .
.
Определим модуль и направление вектора  / ds.
/ ds.
Очевидно, 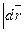 / ds
/ ds  =
= 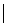
 (
( /
/ 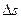 )
)  = 1 как
= 1 как
предел отношения длины бесконечно малой хорды ММ 1 к длине стягиваемой ею дуги. Направление вектора ∆  /∆ s совпадает с направлением с направлением ∆
/∆ s совпадает с направлением с направлением ∆  при ∆ s> 0 и противоположно ему при ∆ s< 0, т. е. вектор ∆
при ∆ s> 0 и противоположно ему при ∆ s< 0, т. е. вектор ∆  /∆ s всегда направлен по хорде ММ1 в сторону возрастания криволинейной координаты s. Поэтому вектор
/∆ s всегда направлен по хорде ММ1 в сторону возрастания криволинейной координаты s. Поэтому вектор  / ds = =
/ ds = =  (
( /
/ 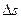 ) направлен по касательной к траектории в сторону возрастания криволинейной координаты s и не зависит от направления движения точки, т. е. вектор
) направлен по касательной к траектории в сторону возрастания криволинейной координаты s и не зависит от направления движения точки, т. е. вектор
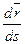 =
= 
представляет собой единичный вектор (орт) касательной к траектории точки, направленный в сторону роста криволинейной координаты s. Тогда вектор скорости точки равен
 =
= 
 =
= 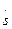
 (1.13)
(1.13)
Производная ds/dt в выражении (1.13) представляет собой проекцию вектора скорости точки на касательную к ее траектории и называется алгебраической скоростью. Условимся обозначать ее через vτ. Тогда алгебраическая скорость точки
vτ =  =
= 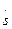 , (1.14)
, (1.14)
а вектор скорости
 = vτ
= vτ  . (1.15)
. (1.15)
Алгебраическая скорость vτ может быть как положительной, так и отрицательной. Если в некоторый момент времени vτ = 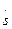 >0, то функция s = f (t) возрастает, т. е. точка движется в сторону возрастания криволинейной координаты s, если vτ< 0, то функция s = f (t) убывает и в этот момент времени точка движется в сторону убывания криволинейной координаты s.
>0, то функция s = f (t) возрастает, т. е. точка движется в сторону возрастания криволинейной координаты s, если vτ< 0, то функция s = f (t) убывает и в этот момент времени точка движется в сторону убывания криволинейной координаты s.
Таким образом, знак алгебраической скорости vτ указывает направление движения точки по траектории. Очевидно, что модуль вектора скорости равен модулю ее алгебраической скорости, т. е. |  | = | vτ |.
| = | vτ |.
1.3. УСКОРЕНИЕ ТОЧКИ
Из предыдущего (п.1.2) следует, что вектор скорости точки в общем случае изменяется с течением времени как по величине, так и по направлению. Ускорение точки характеризует быстроту изменения величины и направления вектора скорости точки. Очевидно, что ускорение точки – величина векторная.
Определение ускорения при векторном способе задания движения.
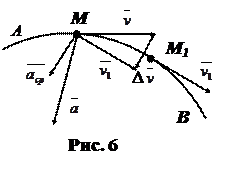 Пусть точка движется по траектории АВ. В момент времени t она находитсявположении М и имеет скорость
Пусть точка движется по траектории АВ. В момент времени t она находитсявположении М и имеет скорость  , а в момент времени t + Δ t она находится в положении М 1и имеет скорость
, а в момент времени t + Δ t она находится в положении М 1и имеет скорость  1 (рис. 6). Найдем приращение вектора скорости Δ
1 (рис. 6). Найдем приращение вектора скорости Δ  за промежуток времени Δ t. Для этого перенесем вектор
за промежуток времени Δ t. Для этого перенесем вектор  в точку М, тогда Δ
в точку М, тогда Δ  =
= 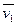 -
-  . Средним ускоре-
. Средним ускоре-
нием точки за промежуток времени Δ t называетсяотношение приращения вектора скорости Δ  к этому промежутку времени Δ t:
к этому промежутку времени Δ t:
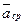 = Δ
= Δ  / Δ t. (1.16)
/ Δ t. (1.16)
Направление этого вектора совпадает с направлением Δ  .
.
Предел среднего ускорения при Δ t→ 0 называется ускорением точки в момент времени t, или просто ускорением точки:
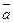 =
=  =
= 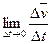 =
=  . (1.17)
. (1.17)
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной по времени от радиус-вектора точки:
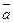 =
=  =
= 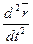 . (1.18)
. (1.18)
Здесь учтено, что  = d
= d  /dt – формула (1.7). Можно также пользоваться следующей формой записи:
/dt – формула (1.7). Можно также пользоваться следующей формой записи: 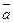 =
= 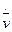 =
= 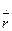 .
.
Определим направление вектора ускорения. Вектор 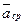 лежит в плоскости, образуемой векторами
лежит в плоскости, образуемой векторами  и
и 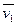 , проведенными из точки М (см. рис. 6). При уменьшении Δ t точка М 1 приближается к точке М, и плоскость (
, проведенными из точки М (см. рис. 6). При уменьшении Δ t точка М 1 приближается к точке М, и плоскость ( ,
, 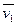 ) в соответствии с изменением направления
) в соответствии с изменением направления 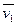 , будет менять свое положение в пространстве, поворачиваясь вокруг вектора
, будет менять свое положение в пространстве, поворачиваясь вокруг вектора  . В пределе при Δ t→ 0 и М 1→ М векторы
. В пределе при Δ t→ 0 и М 1→ М векторы  и
и 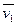 определят плоскость, которая называется соприкасающейся плоскостью кривой (траектории) в точке М. Таким образом вектор ускорения
определят плоскость, которая называется соприкасающейся плоскостью кривой (траектории) в точке М. Таким образом вектор ускорения 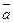 лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории (так как Δ
лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории (так как Δ  направлено в сторону вогнутости).
направлено в сторону вогнутости).
Если кривая плоская, то соприкасающейся плоскостью является плоскость кривой и вектор ускорения лежит в этой плоскости.
Размерность ускорения L/T2, т.е. единицами измерения могут быть м/с2, см/c2.
Определение ускорения при координатном способе задания движения.
Пусть движение точки задано координатным способом, т.е. заданы ее уравнения движения:
x = f1(t), y = f2(t), z = f3(t).
Радиус-вектор  движущейся точки представим в виде
движущейся точки представим в виде
 = x
= x 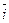 + y
+ y  +z
+z 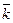 .
.
Так как ускорение точки равно первой производной по времени от вектора скорости движущейся точки или второй производной от ее радиус-вектора, а орты 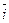 ,
,  ,
, 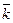 постоянны, то:
постоянны, то:
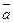 =
=  =
= 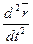 =
= 
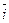 +
+ 
 +
+ 
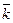 =
= 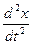
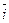 +
+ 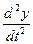
 +
+ 
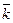 .
.
Разлагаем ускорение на составляющие по осям координат:
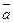
 = ax
= ax 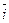 + ay
+ ay  + az
+ az 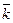 .
.
Сопоставляя обе формулы, определяющие ускорение, получаем:
ax =  =
= 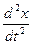 , ay =
, ay =  =
= 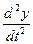 , az =
, az =  =
=  . (1.19)
. (1.19)
Таким образом, проекции вектора ускорения точки на оси декартовой системы координат равны первым производным по времени от проекций вектора скорости на соответствующие оси или вторым производным от соответствующих координат точки по времени.
Формулы (1.19) можно записать и в таком виде:
ax =  =
= 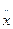 , ay =
, ay = 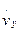 =
= 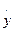 , az =
, az = 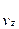 =
=  .
.
Вычислив проекции вектора ускорения на оси координат, находим модуль вектора ускорения:
| 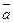 | =
| = 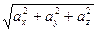 =
= 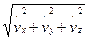 =
= 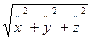 , (1.20)
, (1.20)
и его направляющие косинусы:
cos(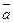 ,
, 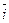 ) =
) = 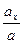 , cos(
, cos(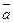 ,
, 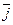 ) =
) = 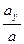 , cos(
, cos(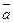 ,
, 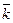 ) =
) = 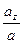 . (1.21)
. (1.21)
Определение ускорения при естественном способе задания движения.
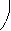 Предварительно остановимся на некоторых геометрических понятиях, изучаемых в дифференциальной геометрии. Рассмотрим пространственную кривую. В точке М кривой проведем касательную М τ (рис. 7). В точке М 1, отстоя-
Предварительно остановимся на некоторых геометрических понятиях, изучаемых в дифференциальной геометрии. Рассмотрим пространственную кривую. В точке М кривой проведем касательную М τ (рис. 7). В точке М 1, отстоя-
щей от точки М на расстоянии Δ s, построим касательную М 1 τ1. Из точки М
проведем линию М  , параллельную М 1 τ1. Угол α между линиями М τ и М
, параллельную М 1 τ1. Угол α между линиями М τ и М 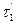 называется углом смежности. Кривизной кривой k в точке М называется предел отношения угла смежности α к приращению криволинейной координаты Δ s, при стремлении Δ s к нулю, т. е.
называется углом смежности. Кривизной кривой k в точке М называется предел отношения угла смежности α к приращению криволинейной координаты Δ s, при стремлении Δ s к нулю, т. е.
k = 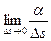 . (1.22)
. (1.22)
Радиусом кривизны кривой ρ в точке М называют величину, обратную кривизне кривой в этой точке, т. е.
ρ = 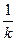 . (1.23)
. (1.23)
Заметим, что кривизна прямой рана нулю, а ее радиус кривизны равен бесконечности. Кривизна окружности во всех ее точках одинакова и равна обратной величине радиуса окружности (k = 1/ R); радиус кривизны равен радиусу окружности (ρ = R).
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 710; Нарушение авторских прав?; Мы поможем в написании вашей работы!