Экспериментальные методы определения динамических свойств объектов

Лекция №13

Известно, что динамические свойства объекта, описываемого линейным дифференциальным уравнением с постоянными коэффициентами, определены, если найдены числовые значения этих коэффициентов либо установлен один из математических операторов преобразования, связывающий входную величину 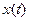с выходной 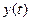. 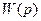К таким операторам, в частности, относятся переходная функция исследуемого объекта , весовая функция передаточная и частотная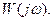

Процедура построения математической модели объекта исследования по реализации его входных и выходных переменных называется идентификацией этого объекта.

Принципиально наиболее простой является идентификация объекта,основанная на физической сущности частотного метода. Известно, что при подаче на вход линейного объекта гармонических сигналов, представленных рядом

(13.1)

на выходе формируется сигнал 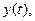который можно выразить аналогичным рядом

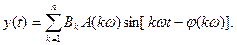(13.2)

Здесь 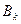- коэффициенты гармонического ряда, , 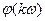- значения амплитудной и фазовой частотных характеристик объекта на частоте , где 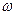- частота первой гармоники.

Экспериментальное определение 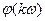производят следующим образом. На вход исследуемого объекта подают гармонические колебания 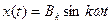. На выходе объекта измеряют амплитуду и фазу колебаний выходной переменной 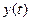. Тогда, как следует из (13.1) и (13.2), отношение амплитуды выходного сигнала к входному определяет значение амплитудно-частотной характеристики для данной частоты , а фазовый сдвиг – значение фазы 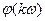. Полученные значения амплитуд и фаз для различных частот входного сигнала позволяют построить частотную характеристику объекта

.

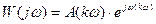Использовав богатые по спектральному составу пробные сигналы.типа ступенчатой функции или импульсной функции, можно резко сократить длительность эксперимента. Наиболее простой метод состоит в том, что на вход объекта подается импульсное возмущение достаточно малой продолжительности. Этот импульс рассматриватся как 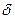- функция (с точностью до постоянного множителя ). Воспользовавшись интегралом свертки

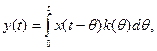(13.3)

можно записать

где - искомая весовая функция.

Вместо импульса на вход объекта можно подать ступенчатый сигнал реакция на который является переходной функцией (с точностью до постоянного множителя ), причем

.

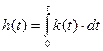Весовая функция в принципе может быть найдена и при произвольных сигналах на входе и выходе объекта. Тогда задача сводится к решению интегрального уравнения вида (13.3). Однако при наличии шумов это выражение малопригодно для определения функции веса, так как основанные на нем методы вычисления не удовлетворяют требованию помехоустойчивости.

Действительно, пусть к объекту приложено не только входное воздействие 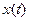, но и помеха . Тогда, тспользуя принцип суперпозиции, имеем

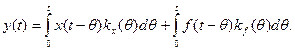(13.4)

Здесь , 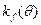- весовые функции объекта по отношению к сигналам 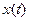и соответственно.

Определить 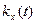из уравнения (13.4) очень трудно, поскольку второй член в правой части этого уравнения является источником погрешности, оценка которой невозможна.

Указанного недостатка лишены статистические методы определения весовой функции, основанные на решении интегрального уравнения Винера – Хопфа.

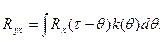(13.5)

Такие методы позволяют по корреляционной функции сигнала на входе 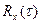и взаимной корреляционной функции между выходным и входным сигналами 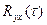найти весовую функцию В данном случае при любом количистве помех, некоррелированных с входны сигналом 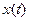, уравнение (13.5) остается справедливым.

Решение уравнения (13.5) обычно сводится к решению системы алгебраических уравнений, формируемых путем замены интеграла суммой и выделения дискретных значений подынтегрального выражения в моменты времени 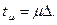Здесь , где 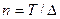, причем 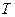- конечный интервал наблюдения; - интервал дискретности. Эта система n +1 уравнений имеет вид

(13.6)

Неизвестными являются дискретные значения 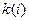импульсной переходной функции Вычислительные алгоритмы для решения системы уравнений высокого порядка вида (13.6) достаточно точно разработаны и могут быть реализованы с помощью средств вычислительной техники. Аналитическое выражение функции может быть найдено путем обработки дискретных значений 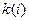методом наименьших квадратов.

Определение весовой функции значительно упрощается, если на вход объекта подать искусственный сигнал типа белого шума, кореляционная функция которого имеет вид 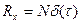. Подставив это выражение в уравнение (13.5), запишем

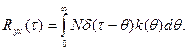(13.7)

Из соотношения (13.7) следует, что при подаче на вход объекта сигнала типа белого шума функция веса с точностью до поставленного множителя совпадает со взаимной корреляционной функцией

Если корреляционные функции заданы в виде аналитических выражений, то, применив к выражению (13.5) преобразования Фурье, получим

(13.8)

Здесь - вщаимная спектральная плотность между выходными и входными сигналами,

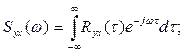
- частотная характеристика объекта,

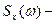спектральная плотность входного сигнала, определенная аналогично по известной корреляционной функции

Как следует из уравнения (13.8), для определения по известным 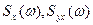нужно воспользоваться следующим соотношениями:

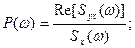
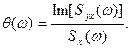
Из всех рассмотренных методов идентификации объектов исследования наиболее распространенными в силу простоты реализации являются методы определения временных характеристик или При использовании таких методов на вход объекта подаются сигналы ступенчатой или импульсной функций. В случае, когда активное вмешательство в ход процесса невозможно или недопустимо, привлекают статистические методы, базирующиеся на решении интегрального уравнения (13.7). 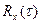При этом необходимой и достаточной информацией для определения весовой функции объекта является знание корреляционных функций и 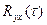, находимых по экспериментальным данным.

Лекция № 14 ОТКРЫТИЕ

Итогом ряда фундаментальных исследований являются научные открытия, т.е. в широком смысле это результат познания, заключающийся в формировании новых научных положений. Открытия расширяют возможности использования человеком сил природы.

Научные открытия как особый объект научного творчества не охранялись правом ни в одной стране до 1947 года. В настоящее время в стране действует система государственной регистрации открытий, имеющая своей целью:

а) подтверждение достоверности научных положений, заявлений в качестве открытия;

б) установление авторского и государственного приоритета открытия;

в) признание заслуг авторов открытий и предоставление им льгот в соответствии с действующим законодательством;

г) содействие в решении н-т. проблем, связанных с открытиями;

д) госучетинформации оботкрытии в целях всестороннего их использования в науке и н.х.

26 июня 1957г − открытие № 1.

Достоинства открытий: сравнительно низкая себестоимость и их долговечность.
Как закон определяет охраноспособное научноеоткрытие?

Юридически открытием признается установление неизвестных ранее объективно существующих закономерностей, свойств и явлений материального мира, вносящих коренные изменения в уровень познания. Это определение называют нормальным (легальным). Оно устанавливает признаки открытия: именно соответствия научного положения установленной совокупности критериев означает, что в случае имеется охраноспособное открытие.
Не подлежат охране: открытия географические, археологические, полеантологические, открытия полезных ископаемых, открытия в области обществененных наук, а также:

а) отдельные факторы, частные зависимости, а также закономерности, свойства и явления, не вносящие коренных изменений в уровень познания;

б) гипотезы в частности, предположительные представления о строении материи, о происхождении планет, полезных ископаемых, о существовании различных силовых полей и т.п.;

в) решения математических задач, установление абстрактных числовых зависимостей, доказательства различных математических теорем и т.п.;

г) результаты, уточняющие уже известные положения, например, формы небесных тел, их орбиты, а также другие уточнения значений исследуемых величин;

д) утверждения, противоречащие научно-обоснованным и экспериментально подтвержденным мировой наукой;

е) результаты н-и и проектно-конструкторских работ, относящиеся к созданию различных новых тех. процессов и т.д., штаммы микроорганизмов и другие положения, т.е. касающиеся предмета возможных заявок на предполагаемые изобретения;

ж) обнаружение и выведение новых видов растений, животных и микроорганизмов.

Признаки юридически значимого открытия:

Открытие − это констатация научных фактов; это установление объективно существующих закономерностей, свойств и явления материального мира;

мировая (абсолютная новизна ) − "неизвестные ранее закономерности, свойства и явления";

существенность нового научного положения: оно должно вносить коренные изменения в уровень познания;

значительность, весомость вклада в научные познания: это есть коренные изменения;

достоверность открытия − это установление объективно существующих закономерностей, свойств и явлений.

Термин "установление" означает выявление, обнаружение, констатацию определенного рода факторов, т.е. решение задач познания.

Дата добавления: 2014-11-06