Лекция №10

МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА (первое занятие)

При проведении экспериментальных исследований могут решаться две основные задачи:

1. Выявление количественных закономерностей, устанавливающих отношение между переменными, которые описывают объект исследования.

2. Нахождение значений переменных, обеспечивающих оптимальный (по определенному критерию) режим функционирования объекта.

Планирование эксперимента состоит в выборе числа и условий проведения опытов, позволяющих получить необходимые знания об объекте исследования с требуемой точностью. Одним из главных условий поставленного эксперимента является минимизация общего числа опытов. Уменьшение числа опытов не должно существенно отражаться на качестве получаемой информации.

Рассмотрим сущность планирования эксперимента. Остановимся на выборе входных и выходных переменных. Входные переменные х_i, i= , определяющие состояние объекта, называют влияющими факторами.

Выходные переменные У - это реакция объекта на входные воздействия; она носит название функции отклика или цели.

Если аналитическую зависимость, связывающую функцию отклика Y с влияюшими факторами Х_i, найти невозможно и вид функции y=f(x, a₁, a₂, a₃,…) априори неизвестен, то целесообразно использовать степенной ряд

(10.1)

где k - количество влияющих факторов; 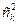- число сочетаний из k элементов по два,

.

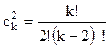Коэффициенты уравнения (10.1) можно определить на основании эксперимента. По результатам каждого эксперимента путем подстановки x_iu и У_u (u – номер эксперимента) в (10.1) можно записать одно уравнение, в котором коэффициенты аппроксимирующего полинома неизвестны. Если число опытов совпадает с числом коэффициентов в аппроксимирующем полиноме, можно составить систему уравнений, решение которой дает значения искомых коэффициентов.

Выбор области экспериментирования (определения)

Граница этой области по каждому фактору x_i обусловлена его минимальным и максимальным значениями, т.е. x_iмин £ x £ x_iмакс.

Область определения функции для случая учета двух факторов (x₁ и x₂) изображена на рис. 10.1.

Для удобства обработки и интерпретации результатов эксперимента целесообразно все факторы представить в безразмерной форме. Для этого производят операцию линейного преобразования факторного пространства - операцию кодирования. Начало координат факторного пространства переносят в точку с координатами (центр эксперимента, на рис. 3.1 - точка 0`), где

.

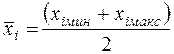Кроме того, интервал варьирования факторов I_i=0,5(x_iмакс–x_iмин) разбивается на ряд уровней, симметричных относительно центра эксперимента. В случае составления симметричных

Рисунок 10.1

двухуровневых планов все k факторов изменяются на двух уровнях. При этом значениям x_iмакс отвечает кодированная переменная x_i=+1, а значениям x_iмин соответствует x_i=–1. Для количественных факторов связь между физическими (Х_i) и кодированными (x_i) значениями факторов определяется соотношением

.

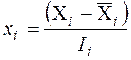Описанные преобразования являются линейными, поэтому в аппроксимирующей функции (10.1) изменяются только координаты при факторах, т.е.

. (10.2)

Здесь x_i - влияющие факторы в безразмерной форме (независимые переменные).

Пусть в уравнении (10.2) рассматривается S членов полинома второго порядка.

Обозначим произведения факторов, а также их квадраты символом x_r (зависимые переменные), а коэффициенты при них символом b_r, где r принимает значения от k+1 до S-1. Тогда получим

Кроме того, при коэффициенте b₀ введем фиктивный фактор x₀=1. В результате уравнение (10.2) будет иметь следующий вид:

(10.3)

Дата добавления: 2014-11-06