Оценка значимости коэффициентов аппроксимирующей зависимости, взятой в виде алгебраического полинома

Оценку проводят для каждого коэффициента a_l с помощью критерия Стьюдента

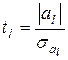. (9.6)

Здесь 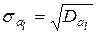, где D_al - дисперсия коэффициента регрессии a_l.

Величины D_al определяем следующим образом. Правые части уравнений (9.4) 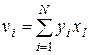не заменяются их числовыми значениями. В результате решения (9.4) для коэффициентов a_l находятся линейные зависимости от величины v_i. Если в эти уравнения (2.4) подставить вместо v_i единицу, а вместо a_l значение M_l, с помощью которого и находят D_al:

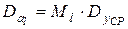, (9.7)

где 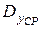определяется по (8.13).

Значение t_l, определенное по формуле (8.15), сравнивается с табличным, найденным для числа степеней свободы r =N(m-1) при принятом уровне (см. приложение 3) значимости. Если t_l>t_T, коэффициент a_l считается незначимым (т.е. можно принять a_l=0) и соответствующее слагаемое исключается из уравнения регрессии. При m=1 имеем v=0 и рассматриваемый метод оценки неприменим. В этом случае оценка значимости коэффициента может быть произведена путем сравнения дисперсий адекватности D_ya при наличии члена аппроксимирующего полинома с коэффициентом a_l и при его отсутствии. Если дисперсия для второго варианта близка к дисперсии для первого (или меньше), то рассматриваемый коэффициент можно считать незначимым.

Пример. Необходимо на основании минимально возможного числа опытов определить аппроксимирующую зависимость w_*=f(M_*) относительной угловой скорости 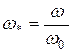от величины относительного момента 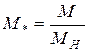искусственной механической характеристики асинхронного двигателя в виде полинома функции.

В соответствии с (8.12) минимальное число опытных точек, при которых можно вычислить дисперсию адекватности 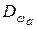, составляет N_мин=S+1. С увеличением N точность описания повышается, но стоимость эксперимента увеличивается. Будем считать достаточным количество опытов, при котором 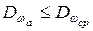, где - дисперсия опыта.

В общем случае, когда нет возможности предсказать степень аппроксимирующего полинома, эксперимент проводится в несколько этапов, число которых зависит от конкретного вида получаемой кривой. На этих этапах последовательно проверяется гипотеза о пригодности полиномов первого, второго и более высоких порядков в качестве уравнений, описывающих процесс.

Будем считать, что погрешность задания значений М_* пренебрежимо мала, а погрешность измерения величины w_* составляет 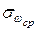=0,01. Величина М_* изменяется в пределах М_мин<M<М_макс, где М_мин=0, М_макс=3.

В первой серии опытов аппроксимирующую зависимость будем искать в виде

.

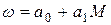При этом N_мин=3; S=2 (определяем 2 коэффициента a₀ и a₁).

Исследуемую область изменения момента разделим на два участка. Тогда шаг изменения момента

.

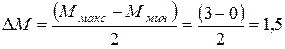Для упрощения вычислений введем относительную величину

,

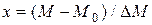где М₀ - начальное значение измеряемого параметра (момента). Если во всей исследуемой области изменения момента до проведения опыта нет причины предпочесть определенное значение М, то в качестве М₀ можно взять среднюю точку М₀=(М_макс–М_мин)/2. В данном случае М₀=1,5. Тогда

;

; .

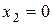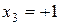Ставим опыты 1 – 3 при этих значениях х и результаты измерений w=w_э заносим в табл.9.5.

Для вычисления коэффициентов a₀ и a₁ воспользуемся методом наименьших квадратов, решив систему нормальных уравнений

;

.

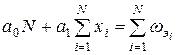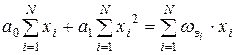В рассматриваемом случае 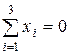; 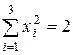и, следовательно,

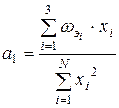; . (9.8)

Заметим, что в данном случае коэффициенты а₀ и а₁ независимы, что резко упрощает вычислительные процедуры и позволяет рассчитать не зависящие друг от друга статистические оценки коэффициентов.

Таблица 9.1 – Данные эксперимента и результаты расчета

№ опыта i	Значение момента М*	Значение х	Экспериме- нтальное значение wэ	Расчетные значения критерия wр	Отклонение Dw=wэ–wр
I серия S=2	II серия	I серия S=2	II серия
I серия	II серия	S=2	S=3	S=2	S=3
		-1	-2		0,927	1,083	0,964	0,073	-0,083	0,036
	0,75	-	-1	0,9	-	0,887	0,948	-	0,013	-0,048
	1,5			0,78	0,647	0,691	0,812	0,133	0,089	-0,022
	2,25	-		0,62	-	0,495	0,556	-	0,125	0,064
				0,16	0,367	0,299	0,18	-0,207	-0,139	-0,02

Исходя из соотношений (2.14) и данных табл. 2.5, получаем а₀=0,647; а₁=-0,28. Тогда в первом приближении имеем

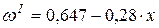. (9.9)

В соответствии с (8.15) определим расчетное значение w_р и занесем его в табл. 9.5. Отклонения Dw_i служат для проверки вычислений: 0. Нанесем опытные точки и аппроксимирующую прямую на график (рис. 9.1). Даже визуальный анализ графика показывает, что опытные и расчетные точки значительно отстоят друг от друга.

При этом

,

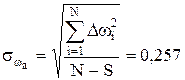и, следовательно, аппроксимация (8.15) неадекватно отражает изучаемую зависимость либо в силу каких-то причин результаты опытов оказались экстенсивными (резко отличающимися от средних). Последняя гипотеза маловероятна, так как Dw_макс<3 , но окончательно ее можно отвергнуть, лишь поставив дополнительные опыты.

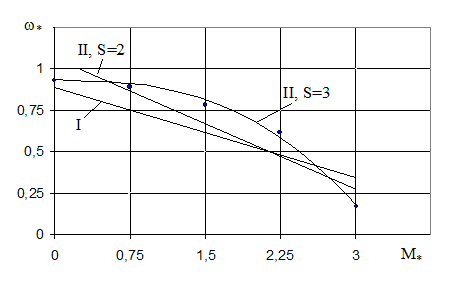
Рисунок 9.1

Проведем II серию опытов (опыты 4 – 5), уменьшив шаг изменения параметра М (момента) вдвое, т.е. взяв N=5. Тогда DM=0,75. При заполнении табл. 2.5 учтем, что при изменении шага DM меняются и значения х. Принимая во внимание результаты I серии опытов, дополнительно ставим два опыта в точках М₄=0,75 (x₄=-1) и М₅=2,25 (x=+1). Записав результаты этих опытов, по формулам (2.14) найдем коэффициенты полинома первой степени: а₀=0,691 а₁=-0,196. Тогда

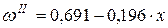. (9.10)

Определим в соответствии с уравнением (8.16) расчетные значения w_pi для всех значений x_i (табл. 9.1). Результаты расчета показывают, что существенного улучшения аппроксимации при увеличении количества опытов не получено (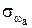 =0,129). В связи с этим перейдем к аппроксимации искомой зависимости полиномом второй степени:

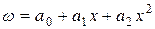. (9.11)

Отметим, что условие N_мин=S+1£N выполняется (S=3 - количество постоянных уравнения (8.17), N=5 - количество точек эксперимента). Коэффициенты полинома (8.17) вычислим, решив систему нормальных уравнений 8.18.

Дата добавления: 2014-11-06