Составление планов первого порядка

Обработка результатов эксперимента

Лекция №11

МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА (второе занятие)

1. На основании данных параллельных наблюдений с помощью формулы (10.11) оценивается дисперсия воспроизводимости D_yi для каждой строки плана, а затем в соответствии с выражением (2.12) определяется критерий Кохрена G и осуществляется проверка однородности дисперсий. В соответствии с выражением (2.13) находится дисперсия опыта.

2. Устанавливаются коэффициенты аппроксимирующего полинома b_i (коэффициенты регрессии) путем решения системы нормальных уравнений вида (2.2).

Производится проверка гипотезы об адекватности модели исходя

3. критерия Фишера F, определяемого уравнением (2.14).

4. Реализуется проверка значимости коэффициентов полинома b_i с помощью критерия Стьюдента t, определяемого в соответствии с соотношением (2.16).

5. Из рассмотрения исключаются незначимые коэффициенты и осуществляется повторная проверка адекватности модели, учитывающей только значимые факторы.

Анализ результатов эксперимента завершается интерпретацией модели в терминах объекта исследования. Выясняется, в какой мере каждый из факторов влияет на функцию отклика. Линейные коэффициенты полинома b_i (при отсутствии других членов) являются частными производными функции отклика по соответствующим переменным, и значение данных коэффициентов служит количественной мерой, оценивающей влияние факторов. Чем больше коэффициент b_i, тем сильнее это влияние. Знак коэффициента позволяет судить о характере зависимости функции отклика от соответствующих факторов.

В данном случае модель объекта включает в себя лишь линейные эффекты и эффекты взаимодействия. Чтобы получить информацию, необходимую для определения коэффициентов полинома, достаточно провести полный факторный эксперимент при двух уровнях факторов, т.е. реализовать план ПФЭ 2^k.

В качестве примера рассмотрим составление плана ПФЭ 2². При этом число опытов N=2²=4. Матрица планирования представлена в табл. 10.1.

В первом столбце матрицы введен фиктивный фактор x₀=1 (при коэффициенте полинома b₀). Столбцы матрицы x₁ и x₂, обведенные рамкой, задают планирование – по ним непосредственно определяются условия опытов, а столбец x₃ не является самостоятельным и заполняется по данным столбцов х₁ и х₂. Он, как и столбец х₀, используется при расчетах.

Коэффициенты аппроксимирующего полинома определяются по формулам

(10.5)

критерия Фишера F, определяемого уравнением (2.14).

6. Реализуется проверка значимости коэффициентов полинома b_i с помощью критерия Стьюдента t, определяемого в соответствии с соотношением (2.16).

7. Из рассмотрения исключаются незначимые коэффициенты и осуществляется повторная проверка адекватности модели, учитывающей только значимые факторы.

Анализ результатов эксперимента завершается интерпретацией модели в терминах объекта исследования. Выясняется, в какой мере каждый из факторов влияет на функцию отклика. Линейные коэффициенты полинома b_i (при отсутствии других членов) являются частными производными функции отклика по соответствующим переменным, и значение данных коэффициентов служит количественной мерой, оценивающей влияние факторов. Чем больше коэффициент b_i, тем сильнее это влияние. Знак коэффициента позволяет судить о характере зависимости функции отклика от соответствующих факторов.

Пример 3.1. Составить матрицу эксперимента ПФЭ 2³.

Зададимся моделью объекта. Будем считать, что модель, учитывающая линейные эффекты и парные взаимодействия, достаточно точно описывает объект. Поэтому модель объекта будет иметь следующий вид:

.

Наиболее простой план, допускающий оценку всех коэффициентов такой модели (S=7), - ПФЭ 2³ (N=8). В этом случае матрица планирования ПФЭ 2³ имеет вид, показанный в табл. 3.2.

Таблица 3.2 – Матрица планирования трехфакторного эксперимента

№ опыта	х0	х1	х2	х3	х1×х2	х1×х3	х2×х3	У
	+1 +1 +1 +1 +1 +1 +1 +1	–1 +1 –1 +1 –1 +1 –1 +1	–1 –1 +1 +1 –1 –1 +1 +1	–1 –1 –1 –1 +1 +1 +1 +1	+1 –1 –1 +1 +1 –1 –1 +1	+1 –1 +1 –1 –1 +1 –1 +1	+1 +1 –1 –1 –1 –1 +1 +1	У1 У2 У3 У4 У5 У6 У7 У8

Число коэффициентов данной модели объекта равно семи, а количество опытов - восьми. ПФЭ 2³ дает в этом случае избыточную информацию.

Пример 3.2. Рассмотрим объект, предназначенный для получения гальванического покрытия с минимальными внутренними напряжениями, при которых обеспечивается необходимая прочность покрытия. Внутренние напряжения могут быть измерены по деформации металла. В результате эксперимента необходимо выяснить, каким образом на внутренние напряжения, принятые в качестве функции отклика, влияют различные факторы.

Предварительные исследования показали, что наибольший интерес представляют следующие три фактора: плотность тока х₁, температура раствора х₂ и концентрация в нем определенного вещества. Уровни факторов и их интервалы варьирования (табл. 3.3) выбраны на основе апприорных сведений об объекте.

Таблица 3.3 – Уровни и интервалы варьирования факторов

Параметры	Факторы
Плотность тока х1, А/дм^2	Температура х2, °С	Концентрация х3, кг/м^2
Основной уровень	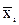		0,7
Интервал варьирования Ii			0,3
Верхний уровень xiмакс			1,0
Нижний уровень xiмин			0,4

Анализ имеющихся сведений об объекте свидетельствует о том, что наибольший интерес представляют линейные эффекты и парные взаимодействия. Поэтому модель объекта имеет вид

.

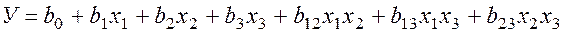Наиболее простой план, допускающий оценку всех коэффициентов такой модели (S=7) - ПФЭ типа 2³ (N=8). Он показан в табл. 11.4. Там же приведены результаты опытов(при m=2), а также расчетные средние значения и дисперсии отклика в каждой точке опыта. Во втором столбце табл. 11.4 указана последовательность проведения опытов (от первого до шестнадцатого), удовлетворяющая требованиям рандомизации (процесс организации случайной последовательности опытов).

Таблица 11.4 – Последовательность, план и результаты эксперимента

№ опы та u	Последователь- ность проведения опытов	Факторы	Отклики	Оценки
х0	х1	х2	х3	У^I	У^II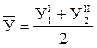
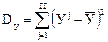
	8;13 11;15 6;14 3;12 2;4 1;9 5;7 10;16	+1 +1 +1 +1	–1 +1 –1 +1 –1 +1 –1 +1	–1 –1 +1 +1 –1 –1 +1 +1	–1 –1 –1 –1 +1 +1 +1 +1	3,40 –0,40 2,70 2,35 2,20 –0,84 0,60 0,60	4,10 –0,60 1,80 3,15 3,30 –1,16 0,90 0,40	3,75 –0,50 2,25 2,75 2,75 –1,00 0,75 0,50	0,245 0,020 0,405 0,320 0,605 0,051 0,045 0,020

По данным табл. 11.4 определим критерий Кохрена:

.

Табличное значение G_T при m–1=1 и N=8 равно 0,680 (приложение 2). Так как G=0,35<G_T=0,68, гипотеза воспроизводимости не отвергается. При этом дисперсия опыта

.

Для определения коэффициентов регрессии воспользуемся выражением (3.5). Тогда в соответствии с данными эксперимента получим:

=1,406.

Аналогично найдем: b₁=–0,968; b₂=0,156; b₃=–0,656; b₁₂=1,031; b₁₃=–0,031; b₂₃=–0,281. Аппроксимирующий полином имеет вид

.

Воспользовавшись приведенной зависимостью, составим табл. 11.5.

Таблица 11.5 – Данные для расчета дисперсии адекватности

№ опыта u		Ур
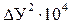
	3,75 –0,50 2,25 2,75 2,75 –1,00 0,75 0,50	3,593 –0,343 2,405 2,593 2,905 –1,155 0,593 0,657	–0,157 0,157 0,155 –0,157 0,155 –0,155 –0,157 0,157	246,49 246,49 240,25 246,49 240,25 240,25 246,49 246,49

Исходя из данных табл. 11.5 найдем дисперсию адекватности

.

Для проверки гипотезы адекватности вычислим значение критерия Фишера:

.

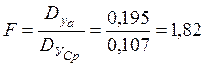При числе степеней свободы r₁=8–7=1 и r₂=8(2–1)=8 согласно приложению 1 F_T=5,32>F=1,82. Следовательно, гипотеза об адекватности выбранной модели не отвергается.

Далее найдем значимые коэффициенты регрессии. Дисперсия коэффициентов определяется в соответствии с (2.17) и с учетом (2.13). Для ортогонального двухуровневого плана эти дисперсии одинаковы для всех коэффициентов:

.

Среднеквадратичные отклонения

.

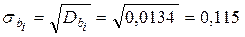Расчетное значение критерия Стьюдента для коэффициента b₀ устанавливаются по формуле (2.16)

.

Аналогичным образом вычислим значения t-критерия для коэффициентов t₁=8,43; t₂=1,36; t₃=5,72; t₁₂=8,98; t₁₃=0,27; t₂₃=2,44.

Табличное значение критерия Стьюдента, определенное по таблице (приложение 3), для числа степеней свободы r = N(m–1)=8(2–1)=8 составляет t_T=2,31. Сравнение расчетных значений t-критерия с табличным позволяет сделать заключение о незначимости коэффициентов b₂ и b₁₃. Тогда уравнение аппроксимирующего полинома примет вид:

.

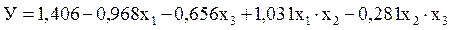Найдем дисперсию адекватности для данного случая. Окончательно получим:

.

Здесь значение критерия Фишера F=0,133/0,107=1,24. Значение этого критерия, найденное в приложении 1 при r₁=8–5=3 и r₂=8(2–1)=8, составляет F_T=4,07 и, следовательно, гипотеза об адекватности модели и в данном случае не отвергается.

Заметим, что когда необходимо оценить адекватности модели во всей области экспериментирования, следует поставить контрольные опыты вне точек эксперимента, например в точке х₁=0. Если погрешность в контрольных точках окажется близкой к погрешности опыта, можно считать, что найденная аппроксимирующая зависимость удовлетворительно описывает исследуемое явление во всей области экспериментирования. Если указанное условие не выполняется, то необходимо изменить план проведения эксперимента, а возможно, и вид аппроксимирующей зависимости.

Дата добавления: 2014-11-06